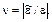Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диаграммы растяжения и основные механическиеСодержание книги
Поиск на нашем сайте
характеристики материалов
Для экспериментов на растяжение выработаны стандартные круглые образцы (рис.5.1), в которых выделяются: рабочая часть 1 (между рисками), конусные части 2, головки 3, закладываемые в захваты машины 4. Наряду с длинными образцами (l =10 d) применяются короткие образцы (l =5 d). Плоские образцы из листового материала имеют те же соотношения между длиной и площадью поперечного сечения, что и круглые образцы.
формациями ε и отражающей теперь Рис. 5.1 уже свойства самого материала. Для определения напряжений силу обычно относят к начальной площади сечения образца. Это оправдано при малых деформациях (порядка 1...2%). В
случае больших деформаций вычисляют так называемые истинные напряжения с учетом реальной площади сечения. На рис. 5.2, а показана типичная диаграмма растяжения для малоуглеродистой стали. На первом этапе деформирования (участок ОА диаграммы) между величинами σ и ε наблюдается линейная зависимость, которая сохраняется и при убывании нагрузки. Свойство твердых тел изменять свою форму и объем под влиянием физических воздействий, связанных с возникновением внутренних сил, и полностью восстанавливать первоначальное состояние после устранения этих воздействий называется упругостью. Можно сказать, что линейному физическому закону сопутствуют упругие свойства материала. Как видно из диаграммы, на участке ОА σ = εtgα.
Рис. 5.2
После определения числа tgα = Е на основании обработки эксперименталь-ных данных соотношение приобретает смысл физического закона: σ = Е ε. Его называют законом Гука, по имени английского ученого Р.Гука, который в 1660 г. установил экспериментально пропорциональность силы и удлинения. Коэффициент пропорциональности Е называют модулем продольной упругости (модулем Юнга). Он представляет собой важнейшую характерис-тику упругости материала. Так как деформация ε является безразмерной величиной, то размерность модуля упругости совпадает с размерностью напря-жений. Для стали обычно принимают Е = 2∙105 МПа, для алюминиевых сплавов – 0,7∙105 МПа. Другой механической характеристикой поведения растягиваемого образца в линейной стадии деформирования является коэффициент поперечной дефор- рмации, представляющий собой отношение линейной поперечной деформации
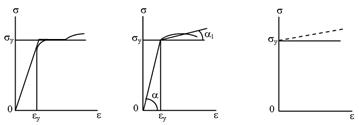
Он введен французским ученым С.Пуассоном и носит его имя. Каждый материал имеет свой коэффициент поперечной деформации. Значения коэффициента Пуассона находятся в пределах от 0 (пробка) до 0,5 (каучук, парафин). Для стали ν = 0,25...0,33, для бетона ν = 0,16...0,18. Наибольшее напряжение, при котором еще справедлив закон Гука, называется пределом пропорциональности (σ pr, точка А на рис. 5.2, а). При дальнейшем увеличении нагрузки диаграмма становится криволинейной. Рост деформации идет быстрее роста напряжений. На участке АВ материал по-прежнему деформируется упруго. Верхняя граница этого участка называется пределом упругости (σ e, точка В на рис. 5.2, а). Наблюдения показывают некоторое отставание деформаций от напряжений. Часть деформации, предусмотренной упругим законом, происходит в процессе возрастания нагрузки, а другая часть – в течение некоторого отрезка времени после прекращения роста нагрузки. Такое явление называется упругим последействием при нагружении. В момент снятия нагрузки деформация исчезает не полностью, а продолжает уменьшаться еще некоторый отрезок времени, доходя до нуля (упругое последействие при разгрузке). При напряжениях, превышающих предел упругости, наблюдаются качественные изменения материала. Если с некоторой точки L (см.рис. 5.2, а) будем разгружать образец, то диаграмма пойдет по прямой LL 1, параллельной прямой ОА. Отрезок OL 1 определяет остаточную, или пластическую деформацию ε р, а отрезок L 1 L 2 − упругую ε е. Полная деформация ε = ε e + ε р характеризует упругопластическое состояние. Ее составляющие не равноценны. Если упругая деформация для металлов составляет 0,2...0,8%, то пластическая деформация может достигать 20% и более. В то же время упругая деформация эластомеров (каучуков) может превышать 100%. Необратимые пластические деформации в незначительной мере могут возникать еще до достижения напряжениями предела упругости. В этих случаях в качестве предела упругости принимают условное значение σ е, которому соответствует остаточная деформация в пределах 0,001...0,005% (обозначается σ0,001, σ0,005). Возрастание пластических деформаций становится особенно заметным начиная с точки С. На участке СЕ деформация растет при постоянной нагрузке. Напряжение, при котором происходит рост деформации без заметного увеличения нагрузки, называется пределом текучести (σ у, точка С на рис.5.2, а). Участок СЕ называется площадкой текучести (зоной общей текучести). Если на диаграмме отсутствует явно выраженная площадка текучести, за σ у принимается условно величина напряжения, при которой ε р составляет 0,2% (σ0,2). В некоторых случаях устанавливается предел 0,5% (σ0,5). Иногда появляется необходимость различать предел текучести на растяжение σ yt и предел текучести на сжатие σ yc. С момента наступления текучести на образце из малоуглеродистой стали появляются линии примерно под углом 45° к его оси, называемые линиями Людерса-Чернова. Они впервые описаны в 1859г. немецким ученым В. Людерсом и, независимо от него, в 1884 г. русским ученым Д.К.Черновым, который впервые предложил использовать их при экспериментальном изучении напряжений в конструкциях. Линии отражают процесс структурных изменений материала в момент наступления состояния текучести. В пределах одного кристалла пластические деформации возникают за счет сдвига его части по некоторой плоскости на целое число элементов решетки. На примере малоуглеродистой стали было показано, что область пластических деформаций может превосходить область упругих деформаций раз в 200. Поэтому упругопластическая стадия работы материала является большим резервом несущей способности конструкций в пределах допустимых деформаций. За пределами площадки текучести диаграмма вновь поднимается вверх, хотя гораздо более полого, чем раньше. Происходит "самоупрочнение" материала, которое для стали объясняется выделением по плоскостям сдвигов из твердого раствора феррита микрочастиц, затрудняющих дальнейшие смещения. Отношение максимальной силы, которую способен выдержать образец, к начальной площади его поперечного сечения называется временным сопротивлением (σ u, точка D на рис. 5.2, а). Изменение площади сечения образца к этому моменту уже значительно. Истинные напряжения показаны пунктирной линией. Участок диаграммы за точкой D характерен для локальной зоны с так называемой шейкой − местным сужением образца. Напряжения в зоне растут и достигают максимума (точка М' на штриховой линии) в момент разрыва образца (точка М на рис. 5.2, а). Учас-ток DM называют зоной местной текучести, а наибольшее напряжение − пределом прочности. Теоретическое значение предела прочности определяется как 0,1 Е. Обычные материалы имеют далеко не идеальную структуру, что существенно снижает их предел прочности по сравнению с теоретически возможным. В лабораторных условиях выращены нитевидные кристаллы чистых металлов, имеющих структуру, близкую к идеальной. Предел прочности таких материа-лов составляет 0,7...0,8 теоретической величины. Площадь диаграммы ОАВС DMM 2 выражает удельную работу внутренних сил, которая при одном и том же напряженном состоянии для различных материалов может существенно различаться. В связи с этим численно равная ей удельная потенциальная энергия деформации также является механической характеристикой материала. Если после рассмотренной выше разгрузки вновь нагружать образец, то диаграмма пойдет по линии L 1 L, образуя небольшую петлю за счет необратимых потерь энергии деформации (петлю упругого гистерезиса). С точки L диаграмма пойдет так, как будто бы не было разгрузки и повторного нагружения образца. Итак, при нагружении образца выше величины σ y и последующей его разгрузке материал изменил свои свойства: отсутствует площадка текучести, повысился предел пропорциональности и уменьшилась полная деформация при разрыве (L 1 M 2< OM 2). Такое изменение свойств материала, присущее металлам, называется наклепом (нагартовкой). Величины σ u и σ y являются характеристиками прочности материала, поскольку они выражают его способность сопротивляться разрушению, а также необратимому изменению формы (пластической деформации) при действии внешних нагрузок. Характеристиками пластичности материала служат остаточное относительное удлинение образца δ = [(l 1 – l 0)/ l 0]∙100% и остаточное относительное сужение поперечного сечения образца при разрыве ψ = [(А 0 – А 1)/ А 0]∙100%, где l 0 и А 0 – начальные длина образца и площадь его сечения; l 1 – длина образца при составлении его из двух образовавшихся после разрыва частей; А 1 – площадь поперечного сечения разорванного образца в наиболее тонком месте шейки. У мягких сталей величина δ доходит до 30%, а ψ – до 60%. Величина ψ лучше характеризует пластические свойства материала, чем δ, так как не зависит от соотношения размеров образца. Отметим характерную особенность упругопластической деформации, заключающуюся в отсутствии однозначной зависимости между напряжением и деформацией. Одному и тому же напряжению при монотонном возрастании деформации (активной деформации) и при разгрузке (пассивной деформации) соответствуют различные деформации. В этом коренное отличие упругопластической деформации от нелинейной упругой деформации. Рассмотренная диаграмма растяжения (см. рис. 5.2, а) является характерной для так называемых пластичных материалов, т.е. материалов, способных получать значительные остаточные деформации, не разрушаясь. К числу весьма пластичных материалов относятся медь, алюминий, малоуглеродистая сталь и др. Противоположным свойству пластичности является свойство хрупкости − способность материалов разрушаться без значительных остаточных деформаций (δ = 2...5% и меньше). К хрупким материалам относят чугун, высокоуглеродистую сталь, камень, бетон, стекло, стеклопластики и др. Диаграмма растяжения хрупких материлов показана на рис. 5.2, б. Площад- ка текучести отсутствует, шейка не образуется. Разрушению не предшествует ниспадающая ветвь, и растягивающее усилие растет до момента разрушения. При описании свойств таких материалов вводят понятие секущего модуля (см. рис. 5.2, б) Es = σ/ε = tgλ и касательного модуля Et = d σ/ d ε = tgβ. Условно за предел пропорциональности принимают напряжение, при кото-ром значение Et меньше его значения в начале координат, например, на 50%. Деление материалов на пластичные и хрупкие носит условный характер, так как при определенных условиях хрупкие материалы получают пластические свойства (например, стекло при большом всестороннем сжатии) и, наоборот, пластичные материалы приобретают хрупкие свойства (например, сталь при низкой температуре). Поэтому правильнее говорить не о пластичных и хрупких материалах, а об их пластическом и хрупком состоянии (разрушении). С целью упрощения расчетов диаграмма растяжения схематизируется. Если имеется площадка текучести, диаграмму можно приближенно представить состоящей из двух прямых (рис. 5.3, а). Она моделирует идеальный упруго-пластический материал.1
Рис. 5.3 При отсутствии площадки текучести зависимость σ ~ ε также можно представить в виде двух прямых (рис. 5.3, б). Первый участок (0 ≤ ε ≤ ε y) отражает линейно-упругое состояние: σ = Е ε. Второй участок характеризуется уравнением σ – σ y = E 1(ε – ε y), где E 1 = tgα1. Величина E 1 называется модулем упрочнения. Такая диаграмма свойственна большей частью легированным сталям.
. 1Иногда предполагают, что эта диаграмма аппроксимирует не всю действительную диаграмму напряжений пластичного материала, а лишь два его участка - линейно-упругий и площадку текучести. В ряде случаев упругой деформацией по сравнению с пластической можно пренебречь (рис. 5.3, в). До напряжений, не превышающих σ y, тело рассматри-вается как жесткое, при бόльших напряжениях оно считается пластическим. Материал, наделенный такими свойствами, называется жесткопластическим. Эта схема, как и аппроксимация на рис. 5.3, а, используется для построения моделей предельного состояния конструкций.
|
||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.9.9 (0.011 с.) |

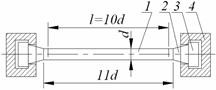 Диаграмма F ~ ∆ l зависит от размеров образца. Однородное состояние рабочей части образца позволяет сделать переход к диаграмме, устанавливающей зависимость между напряжениями σ и линейными де-
Диаграмма F ~ ∆ l зависит от размеров образца. Однородное состояние рабочей части образца позволяет сделать переход к диаграмме, устанавливающей зависимость между напряжениями σ и линейными де-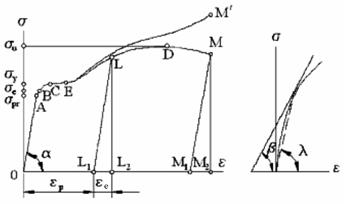
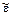 к линейной продольной деформации ε, взятое по абсолютной величине:
к линейной продольной деформации ε, взятое по абсолютной величине: