Ячеечные гидродинамические модели

 

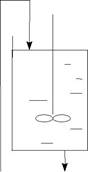
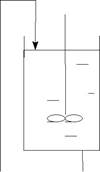
Физическая сущность ячеечной модели заключается в том, что ма-териальный поток может быть представлен несколькими последова-тельно соединенными ячейками, при этом допускается, что в каждой ячейке поток имеет структуру идеального смешения, а между ячейками перемешивание отсутствует.

 

С _вх, v _вх ^{C 1}

 

 

C 1

C2

 

....

 

C ₁ C ₂

 

 

Ci –1

 

C_i

 

...

Ci

 

 

C n –1

 

 

C n –1

 

C _n,

 

Пусть V_i – объем i -й ячейки, м³. Примем V ₁ = V ₂ = V ₃ = … = V_n. Поскольку в каждой ячейке реализуется режим идеального смеше-

 

ния, то для любой ячейки справедливо уравнение МИС:

 

ì

dC 1

=

×(C 0- C 1);

ï

dt

ï

t 1

ï.

ï

ï^.

ï dC

=

×(Ci -1- Ci);

(2.7)

í

i

dt

ti

ï

ï.

ï

ï^.

^ï dC

=

×(C

- C

).

ï

n

t

ï

dt

n

n -1

n

î

Время пребывания вещества в каждой ячейке τ = V_i / v, общее время пребывания τ = V / v, тогда объем всех ячеек V = nV_i, где n – число ячеек.

 

 

Уравнение ячеечной модели для i -й ячейки примет вид

 

dCi	=	n	×(C	- C	),	(2.8)
dt t	i -1	i

при t = 0 C (0) = C ₀.

 

При n = 1 получим модель идеального смешения, при n →∞ – мо-дель идеального вытеснения.

При использовании ячеечной модели очень важно правильно вы-брать число ячеек, которое можно рассчитать по формуле

n = ^Pe ₂ ^D =₂ ^ul_DL.

 

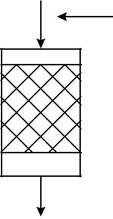
Ячеечные модели достаточно точно отражают свойства потоков

в различных абсорбционных и экстракционных колоннах, в теплооб-

менных аппаратах некоторых конструкций, в каскаде химических реак-торов с мешалками, в аппаратах с псевдоожиженным слоем.

 

Определение условий перемешивания

 

В проточных аппаратах

 

Для того чтобы установить характер перемешивания потока в ап-парате, необходимо на входе в поток ввести какое-либо вещество (ин-дикатор, трассёр) и изучить изменение концентрации этого вещества в выходном потоке, т. е. найти отклик системы на входное возмущение.

 

Индикатором является вещество (азот, аргон, гелий), которое вво-дится в небольшом количестве и отличается по свойствам от других компонентов потока.

 

СО+Н₂ ^N2

 

CH₃OH

 

Для измерения концентрации на выходе из аппарата можно ис-пользовать различные физико-химические методы анализа: хромато-графические, спектральные и др.

 

 

Существует несколько стандартных способов ввода индикатора в поток:

 

· импульсный;

· ступенчатый.

При импульсном вводе индикатор вводится в основной поток за ко-

 

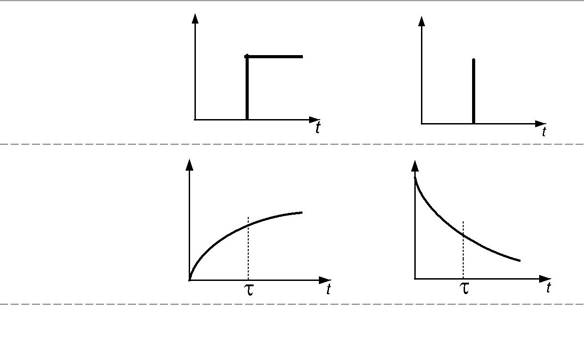
роткий промежуток времени и в небольшом объёме, затем снимается изме-нение концентрации индикатора во времени на выходе из аппарата, т. е. по-лучают кривую отклика системы на импульсное возмущение (С – кривая).

 

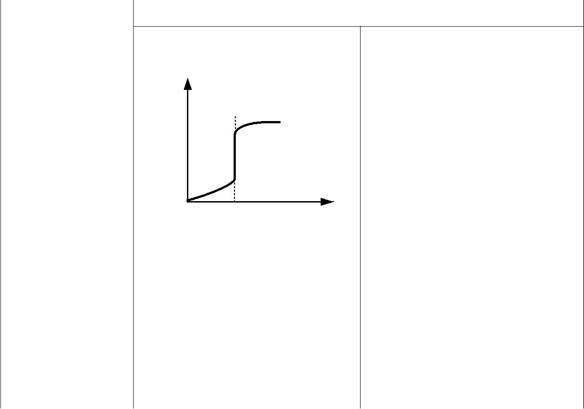
Ступенчатый ввод индикатора предполагает замену части основно-го потока индикатором, при этом на выходе получаем кривую отклика, которая называется F -кривая.

 

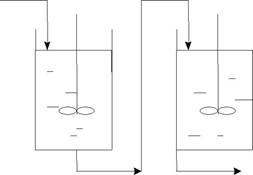
В табл. 2.1 приведены кривые отклика для различных гидродина-мических моделей.

 

	Вопросы для самоконтроля
1.	Назовите типовые	математические	модели	структуры	потоков
	в аппаратах.
2.	Что такое кривая отклика?
3.	Перечислите методы определения гидродинамической структуры
	потоков.
4.	Перечислите модели идеального вытеснения.
5.	Перечислите модели идеального смешения?
6.	Дать характеристику диффузионной модели?
7.	Дать характеристику ячеечной модели?
				Таблица 2.1
	Модель	Характер отклика при возмущении:
	ступенчатом		импульсном
	F(t)		С(t)
Идеального
вытеснения
				t
	F(t)		С(t)
Идеального
смешения

 

		Окончание табл. 2.1
Модель	Характер отклика при возмущении:
ступенчатом	импульсном
	F(t)	С(t)
Диффузионная
	F(t)	С(t)
Ячеечная
	t
	2.2. Моделирование тепловых процессов
	в химической технологии