
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстремумы функций многих переменныхСодержание книги
Поиск на нашем сайте
Решение задачи оптимизации усложняется, если критерий опти-мальности является функцией нескольких независимых переменных. Для непрерывной функции F = F (x 1, x 2,…, xn), имеющей непрерыв-ные производные первого и второго порядков по всем переменным xi (i = 1,…, n), необходимым условием экстремума в точке xi служит ра-венство нулю частных производных по всем переменным, т.е. точки, в которых может быть экстремум функции, определяются решением сис-темы уравнений
Левые части уравнений есть функции факторов x1, …, xn. Поэтому решение системы (4.4) дает оптимальное значение факторов. Если оп-тимизируется технологический процесс, то этому решению соответст-вует оптимальный режим.
Рассмотрим частные задачи оптимизации ХТП с использованием математических моделей.
Оптимизация реактора идеального смешения
В реакторе идеального смешения протекает реакция
Определить оптимальное время пребывания реагентов в реакторе, при котором достигается максимальный выход целевого продукта B (рис. 4.4).
C
CA 0
CB
Рис. 4.4
Составим математическую модель:
dC dt A = t 1 (C A 0- C A)- k 1 CA;
dCdtB = t 1 (C B 0- C B)+ k 1 C A - k 2 CB;
dC dt C = t 1 (CC 0- CC)+ k 2 CB.
Начальные условия: при t = 0 С А (0) = С А 0; С В (0) = С В 0. В стационарном режиме работы реактора
dCdtB = 0;
при CB 0 = 0 уравнение (4.6) примет следующий вид:
- t 1 C B + k 1 C A - k 2 CB =0;
k 1 C A × t = C B + k 2 CB × t; C = k 1 CA × t .
B 1+ k 2 t
Приравниваем к нулю уравнение (4.5):
C A 0- C A - k 1 CAt =0;
C A 0= C A (1+ k 1 t); C = CA 0.
A 1+ k 1 t
(4.5)
(4.6)
(4.7)
(4.8)
(4.9)
Полученное выражение подставим в (4.8):
Для определения оптимального времени контакта (t опт), при котором достигается максимальное значение концентрации СВ, необходимо уравне-ние (4.10) продифференцировать по t и приравнять производную к нулю:
Задача поиска оптимальной температуры
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 172; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.97.1 (0.009 с.) |












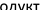




 CA
CA












