О.Е. Митянина, Е.А. Кузьменко

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

 

 

Н.В. Ушева, О.Е. Мойзес,

 

О.Е. Митянина, Е.А. Кузьменко

 

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

 

ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ

 

 

Рекомендовано в качестве учебного пособия Редакционно-издательским советом Томского политехнического университета

 

Издательство

 

Томского политехнического университета

 

 

УДК 66.011:519.876(075.8)

ББК 35.11:22.1я73

М34

 

Ушева Н.В.

 

М34 Математическое моделирование химико-технологических процессов: учебное пособие / Н.В. Ушева, О.Е. Мойзес, О.Е. Митя-нина, Е.А. Кузьменко; Томский политехнический университет. − Томск: Изд-во Томского политехнического университета, 2014. –

 

135 с.

 

В пособии рассмотрена методология построения математических моде-лей химико-технологических процессов; приведены математические модели структуры потоков, кинетики химических реакций, гомогенных химических реакторов, тепловых и массообменных процессов. Рассмотрены подходы по-строения математических моделей экспериментально-статистическими мето-дами, методы корреляционного и регрессионного анализа, методы планирова-ния эксперимента и методы оптимизации.

Предназначено для студентов, обучающихся по направлениям «Энерго-и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии», «Химическая технология», «Биотехнология».

 

УДК 66.011:519.876(075.8)

 

ББК 35.11:22.1я73

 

 

Рецензенты

 

Доктор технических наук, профессор ТУСУРа

 

С.В. Смирнов

 

Кандидат технических наук

заведующая лабораторией Института химии нефти СО РАН

 

Н.В. Юдина

 

 

© ФГБОУ ВПО НИ ТПУ, 2014

© Ушева Н.В., Мойзес О.Е.,

Митянина О.Е., Кузьменко Е.А., 2014

© Оформление. Издательство Томского

 

политехнического университета, 2014

 

 

ОГЛАВЛЕНИЕ

 

ВВЕДЕНИЕ................................................................................................................................................................ 6

 

1. ОБЩИЕ ПРИНЦИПЫ МОДЕЛИРОВАНИЯ.............................................................................. 8

 

1.1. Классификация моделей................................................................................................................ 8

 

1.2. Методология построения математических моделей

химико-технологических процессов................................................................................ 10

 

2. ДЕТЕРМИНИРОВАННЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ

 

ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ..................................................................... 16

 

2.1. Математическое описание

гидродинамической структуры потоков........................................................................ 16

 

2.1.1. Модель идеального смешения................................................................................. 17

 

2.1.2. Модель идеального вытеснения............................................................................. 18

2.1.3. Диффузионные гидродинамические модели............................................... 20

2.1.4. Ячеечные гидродинамические модели............................................................. 21

2.1.5. Определение условий перемешивания

в проточных аппаратах................................................................................................... 22

 

2.2. Моделирование тепловых процессов

в химической технологии........................................................................................................... 24

 

2.2.1. Основные закономерности теплообмена........................................................ 24

2.2.2. Математические модели теплообменных аппаратов............................ 26

2.2.3. Пример моделирования теплообменных процессов............................. 29

 

2.3. Математическое моделирование массообменных процессов..................... 31

 

2.3.1. Математическое описание равновесия

в системе «жидкость-пар» и «жидкость-жидкость»............................... 31

2.3.2. Моделирование процесса массопередачи..................................................... 35

 

2.3.3. Моделирование процесса сепарации................................................................. 37

2.3.4. Моделирование процесса ректификации........................................................ 40

2.3.5. Моделирование процесса абсорбции................................................................ 44

2.3.6. Моделирование процесса адсорбции................................................................ 45

 

2.4. Математическое моделирование кинетики

химических реакций....................................................................................................................... 47

 

2.4.1. Основные понятия химической кинетики....................................................... 47

 

2.4.2. Моделирование кинетики

гомогенных химических реакций.......................................................................... 50

2.4.3. Моделирование кинетики

гетерогенных химических реакций...................................................................... 52

 

2.5. Моделирование гомогенных химических реакторов.......................................... 63

 

2.5.1. Классификация реакторов........................................................................................... 64

 

 

2.5.2. Математическая модель реактора идеального смешения................. 64

2.5.3. Математическая модель реактора

 

идеального вытеснения.................................................................................................. 67

2.5.4. Исследование химического процесса,

протекающего в гомогенном реакторе

идеального смешения...................................................................................................... 69

2.5.5. Исследование химического процесса,

протекающего в реакторе идеального вытеснения

в стационарном режиме................................................................................................. 71

 

3. ЭКСПЕРИМЕНТАЛЬНО-СТАТИСТИЧЕСКИЕ МЕТОДЫ

ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ................................................................. 75

 

3.1. Основные понятия и определения....................................................................................... 75

 

3.2. Статистические модели объектов

на основе пассивного эксперимента.................................................................................. 77

 

3.2.1. Методы корреляционного и регрессионного анализа.......................... 78

3.2.1.1. Линейная регрессионная модель

с одной независимой переменной...................................................... 82

3.2.1.2. Статистический анализ результатов................................................. 83

3.2.1.3. Параболическая регрессионная модель........................................ 86

 

3.3. Статистические модели на основе активного эксперимента

(методы планирования экстремальных экспериментов)................................... 89

 

3.3.1. Планы первого порядка................................................................................................. 89

3.3.1.1. Полный факторный эксперимент......................................................... 89

3.3.1.2. Статистический анализ уравнения регрессии........................... 95

3.3.1.3. Дробный факторный эксперимент...................................................... 96

3.2.3. Статистические модели

оптимальной области объекта исследования 99

 

3.4. Симплексный метод планирования и оптимизации............................................ 107

 

4. МЕТОДЫ ОПТИМИЗАЦИИ В ХИМИЧЕСКОЙ ТЕХНОЛОГИИ........................ 112

 

4.1. Основные понятия и определения.................................................................................... 112

 

4.2. Систематизация методов оптимизации......................................................................... 114

 

4.3. Статистические методы оптимизации............................................................................ 115

 

4.3.1. Метод крутого восхождения по поверхности отклика

(Бокса-Уилсона)................................................................................................................ 115

 

4.4. Аналитические методы.............................................................................................................. 119

 

4.4.1. Оптимизация реактора идеального смешения......................................... 122

4.4.2. Задача поиска оптимальной температуры

обратимой химической реакции.......................................................................... 124

 

4.5. Численные методы решения

оптимизационных задач без ограничений................................................................. 126

 

4.5.1. Одномерная оптимизация......................................................................................... 126

 

4.5.1.1. Метод дихотомии.......................................................................................... 126

 

 

4.5.1.2. Метод золотого сечения 127

4.5.1.2. Метод сканирования 129

 

4.5.2. Многомерный поиск оптимума............................................................................ 130

 

СПИСОК ЛИТЕРАТУРЫ........................................................................................................................... 133

 

 

 

 

ВВЕДЕНИЕ

 

Математическое моделирование – метод исследования процессов или явлений на математических моделях с применением ЭВМ.

 

Современный уровень развития вычислительной техники расширя-ет возможности использования метода математического моделирования при исследовании кинетики гомогенных и гетерогенных химических реакций, лежащих в основе промышленных процессов; выборе типа хи-мического реактора, теплообменного и массообменного оборудования; получении оперативных прогнозов и решении задач оптимизации тех-нологических режимов ведения промышленных процессов действую-щих производств в условиях меняющихся состава сырья и производи-тельности, а также при проектирования технологических схем новых и модернизируемых производств химической промышленности.

 

Процессы, связанные с химической технологией, очень сложны. Это прежде всего химические превращения в аппаратах различных конструк-ций, обусловленных особенностями протекания химических реакций, многокомпонентностью и многостадийностью многих из них, необходи-мостью проведения катализа. Не менее сложны и массообменные про-цессы, в частности процессы ректификации многокомпонентных смесей, широко используемые при подготовке сырья для химических превраще-ний и разделении продуктов реакций либо отделения непрореагировав-ших компонентов сырья от продуктового потока. В настоящее время ши-роко используются совмещенные реакционно-ректификационные процессы как более энерго- и ресурсосберегающие и эргономичные. Теп-лообменные процессы являются неотъемлемой частью любого химиче-ского производства. Их эффективность зависит от конструкций аппара-тов, свойств теплоносителей и ряда технологических параметров.

 

Поэтому важным этапом математического моделирования является создание математической модели, которая бы адекватно описывала рас-сматриваемый процесс. Обычно создаются математические модели от-дельных аппаратов, базирующиеся на моделях процессов, протекающих

 

в этих аппаратах, а затем моделируются технологические схемы, связы-вающие эти аппараты в единый технологический процесс.

 

В зависимости от сложности самого процесса и возможностей по-лучения экспериментальной информации о его прохождении, при раз-работке математических моделей используется либо детерминирован-ный подход, в основе которого лежат фундаментальные законы, либо

 

 

эмпирический, в основе которого лежит статистическая обработка экс-периментальной информации.

Поскольку математические модели могут быть представлены ли-нейными, нелинейными, дифференциальными уравнениями, уравне-ниями в частных производных и их системами, в зависимости от слож-ности моделируемых явлений, необходимо знать и уметь применять численные методы для их решения.

 

Чтобы решение задач оптимизации было реализуемо, нужно пра-вильно определить критерии оптимальности, представить функцию це-ли, задать ограничения на оптимизирующие параметры и грамотно вы-брать метод оптимизации.

 

И наконец, чтобы воспользоваться вычислительной техникой и ре-шить уникальную задачу, связанную с моделированием конкретного химико-технологического процесса, необходимо знать какой-либо из современных языков программирования и уметь работать в соответст-вующей среде, создавая удобный для пользователя интерфейс.

 

Конечно, для решения задач выбора наиболее подходящего чис-ленного метода могут быть привлечены математики, для создания про-граммы с удобным для пользователя интерфейсом – профессиональные программисты, но саму математическую модель должны создавать спе-циалисты предметной области, т. е. специалисты, компетентные в об-ласти химической технологии и промышленной реализации химических

и нефтехимических производств.

 

 

 

Классификация моделей

 

В настоящее время моделирование широко используется в различ-ных областях науки и техники. Широкое применение моделей объясня-ется тем, что модель дает возможность установить в явлении, объекте или процессе основные закономерности, которые им присущи, и пре-небречь второстепенными, вспомогательными признаками [1, 2]. На рис. 1.1 приведена общая классификация моделей.

 

 

Рис. 1.1. Общая классификация моделей

 

В зависимости от характера и сложности явлений могут использо-ваться различные методы моделирования:

 

· геометрический (на основе геометрического подобия величин);

· физический (характеризуется одинаковой физической природой модели и исследуемого объекта);

 

· математический (характеризуется различной физической природой и одинаковым математическим описанием модели и исследуемого объекта).

Процессы химической технологии – это сложные физико-химические

 

системы, имеющие двойственную детерминировано-стохастическую природу, переменные в пространстве и во времени. Особенности дан-ных процессов состоят в следующем [3]:

· в участии многокомпонентных и многофазных материальных потоков;

 

 

· наличии процессов переноса импульса, энергии, массы на границе раздела фаз;

· на процесс в значительной степени влияют геометрические харак-теристики аппарата;

· наложении стохастических особенностей гидродинамической обста-новки в аппарате на процессы массо-, теплопереноса и химического превращения. Это объясняется случайным взаимодействием состав-

 

ляющих компонентов фаз (соударением частиц, коалесценцией) или случайным характером геометрии граничных условий в аппарате. Подобного рода системы характеризуются чрезвычайно сложным

 

взаимодействием составляющих их фаз и компонентов, вследствие чего изучение их с позиции классических детерминированных законов пере-носа и сохранения становится невозможным.

Ключ к решению данной задачи дает применение метода матема-тического моделирования,базирующегося на основе стратегии систем-ного анализа,сущность которого заключается в представлении процессакак сложной взаимодействующей иерархической системы с последую-щим качественным анализом ее структуры, разработкой математическо-го описания и оценкой неизвестных параметров [3].

Математическим моделированием называют изучение свойствобъекта на математической модели, целью которого является определе-ние оптимальных условий протекания процесса, управление им на ос-нове математической модели и перенос результатов на объект [1–4].

 

Математическая модель химико-технологического процесса (ХТП) – совокупность математических структур: формул, уравнений, неравенств

и т. д., адекватно описывающая исследуемые свойства объекта. Реализованная на компьютере математическая модель называется

компьютерной математической моделью,а проведение целенаправ-ленных расчетов с помощью компьютерной модели называется вычис-лительным экспериментом.

Математическое моделирование включает в себя три взаимосвя-занных этапа:

 

· составление математического описания изучаемого объекта. При-менительно к химической технологии математическая модель – со-вокупность математических зависимостей, отражающих в явной форме сущность химико-технологического процесса и связываю-щих его физические, режимные, физико-химические и конструк-тивные параметры;

· выбор метода решения системы уравнений математического опи-сания и реализация его в форме моделирующей программы;

· установление соответствия (адекватности модели объекту).

 

 

В модели должны быть учтены все наиболее существенные факто-ры, влияющие на процесс, и вместе с тем она не должна быть загромож-дена множеством мелких, второстепенных факторов, учет которых только усложнит математический анализ.

В зависимости от конкретной реализации процесса и его аппара-турного оформления, все многообразие химико-технологических про-цессов можно разделить на четыре класса:

· процессы, переменные во времени (нестационарные);

· процессы, не меняющиеся во времени (стационарные);

· процессы, в ходе которых их параметры не изменяются в про-странстве;

· процессы с учетом пространственного изменения параметров.

Так как математические модели являются отражением соответст-

вующих объектов, то они классифицируются аналогичным образом [1–4].

 

Вопросы для самоконтроля

 

1. Дайте определение понятиям «модель», «моделирование». Приве-дите примеры.

 

2. Перечислите виды моделирования, проанализируйте возможности их применения в химической технологии. В чем заключается ос-новная сложность моделирования химико-технологических про-цессов?

3. Назовите два основных вида математических моделей. Приведите примеры.

 

4. В чем отличие стохастических моделей от детерминированных?

5. Перечислите основные этапы математического моделирования.

6. К каким этапам моделирования необходимо вернуться, если расчет на модели показал неадекватный результат?

 

 

 

Математическое описание

 

Модель идеального смешения

 

По данной модели поток представляется в виде непрерывной среды,которая поступает в аппарат и мгновенно распределяется по всему объ-ему аппарата вследствие полного (идеального) перемешивания частиц потока, при этом концентрация и температура остаются постоянными во всех точках объема данного аппарата и на выходе из него [4].

 

С вх

v вх

 

С

 

С вых

 

v вых

 

C _вх= С ₀, n _вх= n ₀при постоянном объеме(V =const).

 

Уравнение материального баланса потоков на входе и выходе из аппарата:

 

I _вх= n С _вх, I _вых= n С _вых,

 

где I – поток вещества [моль/с], v – объемный расход потока, м³/с; С _вх, С _вых, С – концентрация вещества в потоке на входе в аппарат,выхо-де из него и в любой точке объема аппарата соответственно, моль/м³;

V – объем, м³.

В установившемся режиме I _вх = I _вых. Если на входе в аппарат про-

 

изошло изменение концентрации (возмущение), то I _вх ¹ I _вых и в аппарате произойдет накопление вещества. Предположим, что рассматриваемое

 

 

изменение в аппарате произошло за очень маленький промежуток времени D t ® dt,за который в аппарате произойдет накопление массы:∆ М →dM.

 

Разделив обе части уравнения на объем аппарата (V), получим

 

æ М ö

d ç

÷

n

M

V

è

ø

=

×(C 0- C),

= C;

(2.1)

dt

V

V

dC

=

n

×(C 0- C).

dt

V

 

Уравнение (2.1) описывает изменение концентрации в аппарате идеального смешения.

 

Учитывая, что время контакта равно

 

t = V / v,

 

получим модель идеального смешения в следующем виде:

 

dC	=			×(C	- C).	(2.2)
dt	t

Начальные условия: при t = 0 C (0) = C ₀.

 

Гидродинамическая модель идеального смешения является моде-лью с сосредоточенными параметрами, т. к. переменная С изменяется только во времени.

 

Модель идеального смешения (МИС) обычно используют при опи-сании аппаратов, в которых обеспечивается интенсивное перемешива-ние сред. Это аппараты небольших размеров с соизмеримыми высотой

и диаметром. На практике – это аппараты с мешалками барботажного типа либо аппараты с очень высокой скоростью циркуляции потока.

 

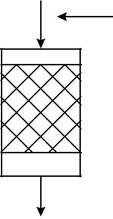
В проточных аппаратах

 

Для того чтобы установить характер перемешивания потока в ап-парате, необходимо на входе в поток ввести какое-либо вещество (ин-дикатор, трассёр) и изучить изменение концентрации этого вещества в выходном потоке, т. е. найти отклик системы на входное возмущение.

 

Индикатором является вещество (азот, аргон, гелий), которое вво-дится в небольшом количестве и отличается по свойствам от других компонентов потока.

 

СО+Н₂ ^N2

 

CH₃OH

 

Для измерения концентрации на выходе из аппарата можно ис-пользовать различные физико-химические методы анализа: хромато-графические, спектральные и др.

 

 

Существует несколько стандартных способов ввода индикатора в поток:

 

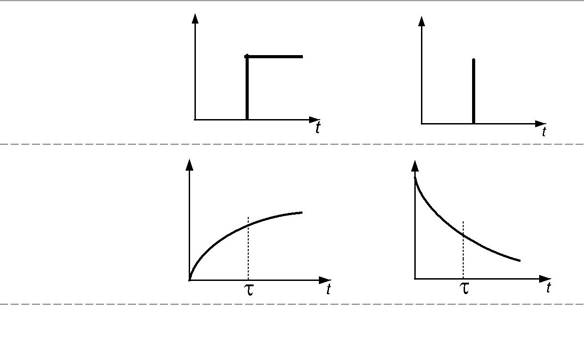
· импульсный;

· ступенчатый.

При импульсном вводе индикатор вводится в основной поток за ко-

 

роткий промежуток времени и в небольшом объёме, затем снимается изме-нение концентрации индикатора во времени на выходе из аппарата, т. е. по-лучают кривую отклика системы на импульсное возмущение (С – кривая).

 

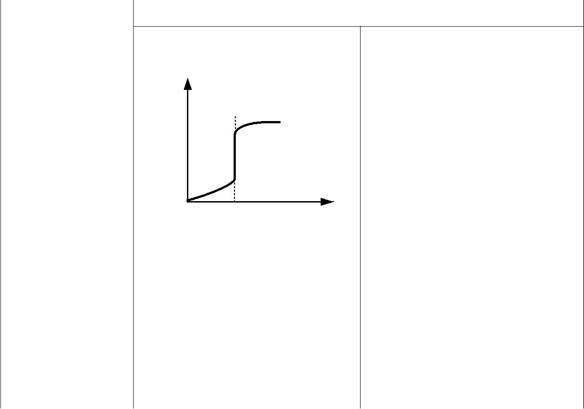
Ступенчатый ввод индикатора предполагает замену части основно-го потока индикатором, при этом на выходе получаем кривую отклика, которая называется F -кривая.

 

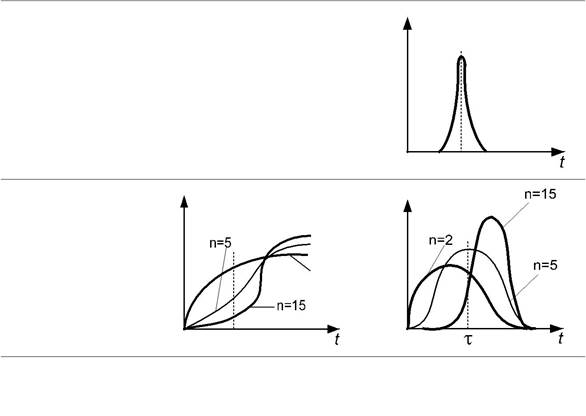
В табл. 2.1 приведены кривые отклика для различных гидродина-мических моделей.

 

	Вопросы для самоконтроля
1.	Назовите типовые	математические	модели	структуры	потоков
	в аппаратах.
2.	Что такое кривая отклика?
3.	Перечислите методы определения гидродинамической структуры
	потоков.
4.	Перечислите модели идеального вытеснения.
5.	Перечислите модели идеального смешения?
6.	Дать характеристику диффузионной модели?
7.	Дать характеристику ячеечной модели?
				Таблица 2.1
	Модель	Характер отклика при возмущении:
	ступенчатом		импульсном
	F(t)		С(t)
Идеального
вытеснения
				t
	F(t)		С(t)
Идеального
смешения

 

		Окончание табл. 2.1
Модель	Характер отклика при возмущении:
ступенчатом	импульсном
	F(t)	С(t)
Диффузионная
	F(t)	С(t)
Ячеечная
	t
	2.2. Моделирование тепловых процессов
	в химической технологии

 

Пример моделирования теплообменных процессов

 

 

(2.15)

 

 

(2.16)

 

В теплообменнике типа «труба в трубе» охлаждается жидкость. Хладоагент и охлаждающаяся жидкость движутся прямотоком.

Необходимо рассчитать температуру теплоносителей на выходе из аппарата и получить температурные профили по длине аппарата.

В табл. 2.2 приведены исходные данные для расчета.

 

		Таблица 2.2
Параметры	Теплоноситель
горячий	холодный
Температура, °С
Объемная скорость, м^3/с	2,3×10^–4	5,1×10^–4
Плотность, кг/м^3
Теплоемкость, Дж/кг×°С	3,35×10^3	4,19×10^3
Диаметр трубы, м	0,01	0,03

 

В теплообменнике реализуется режим «вытеснение-вытеснение», поэтому математическое описание будет иметь вид

 

S × r × C

¶ T 1

= - u

× r

× C

¶ Т 1

+

F 1

× K

×(T - T

);

p 1 ¶ t

p 1 ¶ l

L

T

S

× r

× C

¶ T 2

= - u

× r

× C

¶ Т 2

+

F 2

× K

×(T

- T

).

p 2 ¶ t

L

p 2 ¶ l

T

В стационарном режиме работы теплообменника, когда ∂T ₁ / ∂t = 0; ∂T ₂/ ∂t = 0,уравнения теплового баланса примут следующий вид:

 

 

ì

dT 1

= -

K T × p × d

×(T - T

);

dl

ï

u

× r

× C

p 1

ï

(2.17)

^í dT

K

T

× p

× d

ï

=

×(T 1- T 2),

ï

dl

u 2× r 2× Cp 2

î

где d – диаметр трубы теплообменника, м.

 

Для удобства вычисления введем обозначения:

 

b =	K × p × d	;
		u 1	^× ^r 1 ^× ^C p 1
b =				K × p × d	.
	u 2	^× ^r 2 ^× ^C p 2

Систему полученных дифференциальных уравнений (2.17) решаем с помощью численного метода Эйлера [12]:

ì	i	i -1	i -1	i -1	);
ï ^T 1	= T 1	- hb 1(T 1	- T 2
í						)	,
ï T ^i = T ^i ^-^1+ hb T ^i ^-^1- T ^i ^-^1
î			2 (1

где i – номер шага по длине теплообменника; h – шаг интегрирования по длине теплообменного аппарата.

 

На рис. 2.4 приведены результаты расчета процесса теплообмена.

 

С применением данной математической модели можно выполнить исследования влияния температуры, расхода теплоносителя и хладоа-гента, размеров аппарата на процесс теплообмена.

 

 

Температура, ◦С

 

 

 

 

 

 

 

 

 

 

 

 

 

 

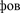
Т ₁ Т ₂