Оптимальной области объекта исследования

 

Полученная на основе ПФЭ или ДФЭ адекватная статистическая модель может быть использована для целей оптимизации ХТП.

 

Применяя один из методов оптимизации (например, метод крутого восхождения), можно достигнуть области оптимума исследуемого про-цесса (почти стационарной области).

После того как достигнута область оптимума, возникает задача ис-следования поверхности отклика.

Описать поверхность отклика оптимальной области линейным уравнением в большинстве случаев невозможно, т. к. велика кривизна поверхности. Для адекватного математического описания требуется многочлен более высокой степени. Наиболее широко для описания об-ласти, близкой к экстремуму, применяют полиномы второго порядка.

 

Естественно, что при возрастании членов уравнениия регрессии должно увеличиваться количество необходимых опытов.

Существует несколько подходов к планированию второго порядка:

1) Варьирование факторов на трех уровнях.

 

В этом случае ПФЭ содержит слишком большое число опытов – 3 ⁿ.

 

Число факторов
Число опытов
Число коэффициентов в уравнении

 

Например, для двух факторов N = 3² = 9 план эксперимента будет следующий:

 

N	x 1	x 2
	+1	+1
	–1	–1
	+1
	–1
		+1
		–1
	–1	+1
	+1	–1

 

2) Использование центрального композиционного планирования эксперимента (ЦКП). Различают два вида ЦКП: ортогональное и рота-табельное. Рассмотрим каждое из них.

 

 

Ортогональное центральное композиционное планирование

 

(ОЦКП) [25].

Центральными планы называют потому, что они симметричны от-носительно центра плана.

Композиционными, – потому что они составляются путем добавле-ния определенного числа опытов к плану первого порядка.

 

Ядром таких планов являются: ПФЭ 2 ⁿ при n <5 (n – число факто-ров) или ДФЭ 2 ^{n –1}(полуреплика от него) при n >5.

 

Если линейное уравнение регрессии в результате статистического анализа оказалось неадекватным, то поступают следующим образом:

 

· добавляют к ядру плана (ПФЭ или ДФЭ) 2 n точек, расположенных на осях координат факторного пространства на расстоянии ± a от центра плана. Эти точки называются «звездными». Координаты

 

«звездных» точек (± a,0,...,0),(0,± a,0,...,0)...(0,0,...± a). Величина a

 

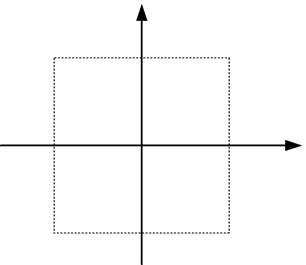
– «звездное плечо».

· увеличивают число экспериментов в центре плана n ₀: точки с коор-динатами (0, …, 0).

На рис. 3.4 приведена схема ЦКП для n = 2.

Точки 1234 – ПФЭ 2²; точки 5678 – «звездные» точки с координа-

тами (± a, 0) и (0, ± a).

 

Количество опытов в матрице ЦКП определяется как

 

N = 2 ^n + 2× n + n 0,если n £5;	(3.45)
N = 2 ^n ^–1+ 2× n + n 0,если n >5.	(3.46)

Построим композиционный план для n = 2 (табл. 3.4).

 

Количество опытов N = 2² + 2×2 + 1 = 9.

 

 

+a

 

 

a

 

-a +a

 

 

-a

 

Рис. 3.4. Схема ЦКП для n = 2

 

 

					Таблица 3.4
N	x 0	x 1	x 2	x 1^2	x 2^2
	+	+	+	+	+
	+	–	+	+	+
	+	+	–	+	+
	+	–	–	+	+
	+	+ a		a ^2
	+	– a		a ^2
	+		+ a		a ^2
	+		– a		a ^2
	+

 

Эта матрица не ортогональная, т. к.

 

å x _{0 j} x ² _ij ¹0;

å x ² _ij x_uj ¹0.

 

Ортогональность композиционных планов достигается выбором значения «звездного плеча» a.

Приведем некоторые значения a для ортогональных планов (n ₀ = 1).

 

n	2(2^2)	3(2^3)	4(2^4)	5(2^5)
a	1.0	1.215	1.414	1.547

 

Уравнение регрессии при ортогональном ЦКП в общем виде будет следующим (например, для двух факторов):

y ˆ= b

^*+ b x

+ b x

+ b

x x

+ b

x ^*+ b

x ^*.

(3.47)

Величины x ₁^* и x ₂^* введены для того, чтобы привести матрицу пла-нирования к ортогональному виду, а коэффициенты b_i определялись не-зависимо друг от друга:

 

			N
xji ^*= x ji	2 -	å ^xji	2 ,	(3.48)
		N j =1

где j – номер опыта, i – номер фактора.

Для того чтобы получить уравнение регрессии в обычной форме:

 

y ˆ= b

+ b x + b x

+ b

x x

+ b

x ^2

+ b

x ^2

,

(3.49)

находят величину

 

*		b	N			b
b 0+ b 0	-		å ^x j 1		-		å ^xj 2	.	(3.50)
N		N
		j =1

 

 

 

Приведем матрицу ортогонального ЦКП для n = 2, a = 1 (табл. 3.5).

 

						Таблица 3.5
N	x 1	x 2	x 1 x 2	x 1^*	x 2^*		y
	+1	+1	+1	0,33	0,33
	–1	+1	–1	0,33	0,33
	+1	–1	–1	0,33	0,33
	–1	–1	+1	0,33	0,33
	+1			0,33	–0,67
	–1			0,33	–0,67
		+1		–0,67	0,33
		–1		–0,67	0,33
				–0,67	–0,67

 

Значения x ₁^* и x ₂^* рассчитываются по формуле (3.47).

 

Например:

 

x ₁₁^*=(-1)²-₉ ⁶ =1-0,67=0,33;

 

x ₅₁^*=1-₉ ⁶ =0,33;

 

x ₅₂^*=0-0,67= -0,67.

 

Для пересчета значений факторов в натуральные единицы пользу-емся формулой пересчета

_{Xi =} ^xi ^{- x}i ⁰_;

D x_i.

 

x_i = X _i × D x_i + x_i ⁰.

 

Матрица (3.5) ортогональная, т. е.

 

å x _{0 j} x_ij ²=0;å x_ij ² x_uj ²=0,

 

но не ротатабельная. Здесь j – номер опыта.

 

Коэффициенты регрессии при ортогональном ЦКП рассчитывают-ся по следующим формулам:

 

1 ^N

^b 0 ^{* =} _N å _{j =1} ^y j ^;

N

	å ^xij ^y j
b =	j =1	;
N
i
	å(xij)^2

j =1

 

			N
			å ^xij ^xuj ^y j	(3.51)
b	=		j =1			;
	N
iu
			å(xij xuj)^2
			j =1
			N
			å x ^* ij y j
b	=		j =1			.
ij			N	(x ^* ij)
		å

i =1

 

Регрессионный анализ уравнения проводится по схеме, приведен-ной ранее. Для расчета дисперсий при определении коэффициентов рег-рессии используют выражения

 

S ^2		* =	^S воспр			;
b	N
	o
S b 0^2= S ^2 b *+	^nSbij	å xji ^2	;
							N
Sb		=
	^S воспр		;
i				N	)2
			å(xji

j =1

 

Sb		=		;	(3.52)
	^S воспр
iu			N
			å(x ji xju)^2

j =1

 

Sb		=	S ^2		;
воспр
ii			N
			å(x ^* ji)

j =1

t_i = ^bj,

^Sbj

 

 

где i ≠ u, i ≠0.

 

Коэффициент значим, если t_j>t _T(q, f₂); f ₂ – число степеней свободы S ²_воспр.Заключительный этап–проверка уравнения на адекватность покритерию Фишера.

 

Ротатабельные планы второго порядка [25]

Ротатабельные планы были предложены в 1957 г. Боксом и Ханте-

ром.

 

Этот метод планирования эксперимента позволяет получить более точное математическое описание поверхности отклика по сравнению

 

с ортогональным ЦКП. Это достигается за счет увеличения числа опы-тов в центре плана и специального выбора величины звездного плеча a.

Приведем некоторые значения a и n ₀ для различного числа факто-ров n.

 

Параметр плана				Количество факторов
Ядро плана	2^2	2^3	2^4	2^5	25–1	2^6	26–1	2^7	27–1
a	1,414	1,682	2,0	2,380	2,0	2,830	2,380	3,360	2,830
n 0

 

Составим матрицу ротатабельного планирования второго порядка для n = 2, a = 1,414, n ₀ = 5 (табл. 3.6).

 

						Таблица 3.6
Nn	x 0	x 1	x 2	х 1 х 2	x 1^2		х 2^2
	+	+	+	+	+		+
	+	+	-	-	+		+
	+	-	+	-	+		+
	+	-	-	+	+		+
	+	+1,414
	+	–1,414
	+		+1,414
	+		–1,414
	+
	+
	+
	+
	+

 

 

Матрица ротатабельного планирования второго порядка неортого-нальна, т. к.

N

å ^x 0 j ^xij

^2 ¹ 0;

j =1

N

å ^xij

^2 xuj

^2 ¹ 0.

j =1

Формулы для расчета коэффициентов имеют вид

2 AB é

n

ù

b 0

=

ê S 0 B (n +

2) - C

å ^Sii ú^;

N

ë

i =1

û

b =

C × Si

;

i

N

(3.53)

C ^2 S

b ji =

ij

;

i ¹ j;

BN

+ C 1- B

S -2 BS ^ü;

b = ^AC ^ì S C é B n +2- n ù

n

ii

í

ii

ë ^(

)

û

(

)å ii

ý

N

î

i =1

þ

А, В, С –константы,которые определяются как

^{A =} 2 B é(n +¹2) B - n ù ^;

ëû

 

B =	n × N	;
(n +2)(N - N 0)
C =	N
	,
	N - N 0

n –число факторов;

 

N –общее число опытов ротатабельного ЦКП; N ₀–число опытов в центре плана.

 

По результатам эксперимента вычисляют суммы:

 

N

S ₀=åy_j;

 

j=1

 

N

S _i =å x _ji y _j; i =1,..., n;

 

N

S _iu =å x_ij x _jk y _j; i ¹ u;

j =1

 

N

S _ii =å x ² _ji y _j.

 

 

Оценки дисперсий в определении коэффициентов вычисляются по следующим формулам:

 

S ^2 b

=

2 AB (n + 2)

S ^2воспр;

N

S ^2 iu

=

S 2

воспр

;(i = 1,..., n);

N - N 0

C

2 S 2

S ^2 b

=

воспр

;

N

iu

S 2

=

AC ^2 S ^2

воспр

é B (n +1)-(n -1)ù.

^bii

N

ë

û

Коэффициенты значимы, если

bi

> Sb t:

N

i

вос