
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Существенности коэффициентов уравненияСодержание книги
Поиск на нашем сайте
Результаты решения представляются в следующем виде:
Таблица 4.2. Параметры уравнений регрессии и их оценка
Результаты решения анализируются на предмет адекватности экономико-статистических моделей реальным причинно-следственным связям. Теснота связи. Выводы о тесноте связи и существенности коэффициентов уравнения делаются на основе представления о порядке вычисления соответствующих показателей. Рассмотрим одну из формул для вычисления множественного коэффициента корреляции. Как правило, компьютерные программы вычисляют множественный коэффициент корреляции R в квадрате. R² – коэффициент детерминации показывает долю систематической дисперсии, то есть вариацию результативного признака. В знаменателе формулы общая дисперсия – это сумма квадратов отклонений фактического значения от среднего значения. Общая дисперсия состоит из систематической и случайной дисперсии.
где
Стандартная ошибка оценки представляет собой случайную дисперсию, распределенную на количество наблюдений, и вычисляется по формуле:
Стандартная ошибка показывает, в каких пределах можно утверждать, что выборочная характеристика имеет место и в генеральной совокупности. Поэтому расчетное значение результативного признака нужно считать нормальным в пределах стандартной ошибки оценки: ŷ ± Δy. Расчетное значение результативного признака следует принимать в пределах от у – Δy до у + Δy. Оценка существенности коэффициентов уравненияпроизводится путем сравнения фактического t -отношения с табличным значением t -критерия Стьюдента. Коэффициент признается существенным, если tх > t0р, где p – вероятность (в экономических расчетах принимается равным 0,95). t -критерий представляет собой отношение значения коэффициента уравнения при переменной к его собственной ошибке:
где μb – ошибка коэффициента регрессии. Если фактическое значение t -статистики больше или равно табличному значению при определенном уровне вероятности, например, p = 0,95, то это значит, что в 95 % случаев изменение факторного признака будет существенно изменять результативный признак. Общая проверка достоверности всех коэффициентов регрессии осуществляется на основе критерия Фишера:
(4.22)
где σсистем. – большой средний квадрат (систематическая дисперсия); σостаточ. – малый средний квадрат (остаточная дисперсия); k1 и k2 – степени свободы: k1 = m (число параметров уравнения, включая свободный член), k2 = n – m -1 (n – число наблюдений). Связь результативного признака со всеми факторными признаками признается существенной, если F > Fр по таблице значений F для заданного уровня вероятности. 4.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

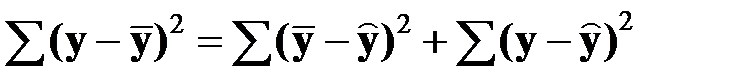 , (4.19)
, (4.19) – общая дисперсия, то есть сумма квадратов отклонений фактического значения от среднего значения;
– общая дисперсия, то есть сумма квадратов отклонений фактического значения от среднего значения; – систематическая дисперсия, то есть сумма квадратов отклонений, вызванных влиянием учтенных факторов;
– систематическая дисперсия, то есть сумма квадратов отклонений, вызванных влиянием учтенных факторов; – случайная (остаточная) дисперсия, то есть сумма квадратов отклонений, вызванных влиянием неучтенных факторов.
– случайная (остаточная) дисперсия, то есть сумма квадратов отклонений, вызванных влиянием неучтенных факторов.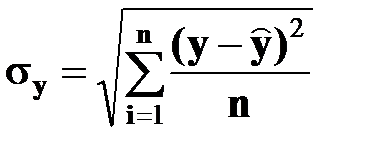 . (4.20)
. (4.20) , (4.21)
, (4.21)


