
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка совокупности наблюдений на нормальностьСодержание книги
Поиск на нашем сайте
Распределения
Корреляционные уравнения описывают зависимость между признаками, которая проявляется в среднем для определенного круга наблюдений. Среди объектов, для которых определяется уравнение, могут быть такие объекты, по которым показатели резко отклоняются от среднего значения признака. Причинами резких расхождений могут быть технические ошибки, а также наличие объектов, качественно отличающихся от остальных и подлежащих самостоятельному изучению (например, предприятие другой специализации). Для уменьшения ошибки оценки необходимо принимать в расчет качественно однородную совокупность. Если статистическая совокупность однородна и не содержит значительных ошибок, то распределение совокупности наблюдений подчиняется закону нормального распределения. При достаточно большом числе наблюдений подавляющая их часть имеет значения признака, близкие к среднему значению (
В пределах значений нормированного отклонения t = ±1 располагается больше половины (68,27 %), t = ±2 – 95,45, t = ±2,6 – 99 % всех членов распределения. О близости фактического и теоретического распределения получают представление на основе критериев согласия. В наибольшей степени соответствуют характеру производственных связей χ² -Пирсона и λ -Колмогорова. Если какие-либо наблюдения нарушают нормальность распределения, то их исключают из расчетов. Более простой способ избавления от "возмущающих" наблюдений визуальный: при просмотре исходной матрицы следует построить ранжированные ряды распределения и исключить наблюдения с показателями, резко отличающимися от средних значений.
Подбор формы связи
Форма связи может быть линейной или криволинейной. Для описания криволинейных зависимостей существует большое количество функций. Экономисту важно описать тенденцию изменения результативного признака при изменении факторных признаков. Поэтому выбор адекватной функции делается из небольшого числа простейших функций путем сравнения статистических характеристик нескольких наиболее подходящих к характеру связи функций. 1. Линейная функция y = b0 + b1х графически представлена на рис. 4.1.
Свободный член b0 представляет собой отрезок, отсекаемый линией регрессии на оси ординат. Параметр b1 – тангенс угла наклона α прямой по отношению к оси абсцисс. Коэффициент b1 показывает, насколько возрастает величина y при увеличении фактора х на единицу.
Предельная отдача фактора равна первой производной по фактору: для линейной функции ¶y/¶x = b1. Коэффициент эластичности (Ex) показывает степень изменения результативного признака при изменении факторного признака на 1 % и определяется как произведение первой производной на отношение значения фактора к расчетному значению результативного признака:
Уравнение прямой обычно применяют в тех случаях, когда с возрастанием фактора х происходит пропорциональное увеличение или уменьшение результативного признака y.
В случае, если предполагается изменение результативного признака тенденции на обратную, то применяют многочлен второй степени (парабола или квадратичное уравнение). 2. Квадратный многочлен (парабола второй степени) y = b0 + b1х + b2x2, Рис. 4.2 Предельная отдача: Коэффициент эластичности: Функция параболы имеет экстремум. Экстремум функции показывает, при каком значении фактора результативный признак имеет максимальное (Ymax) или минимальное значение (Ymin) в зависимости от знака коэффициента b2:
3. Степенная функция Показатель степени данной функции равен коэффициенту эластичности производства, его можно прямо принять за процент изменения y, если х возрастает на 1 %. Если b1 = 1, то y возрастает в той же степени, что и х, при b1 >1 y возрастает в большей степени, а при b1 <1 – в меньшей степени, чем х. После линеаризации степенная функция принимает следующий вид:
Недостатком данной функции является то, что на любом уровне затрат продукция возрастает на один и тот же процент, то есть не отражает закон убывающей отдачи. Функция не имеет экстремума.
Первая производная (предельная отдача фактора) находится так:
4. Все три варианта характера изменения результативного признака при изменении факторного признака описывает кинетическая функция, которая получена на основе экспоненциальной функции. В экспоненциальную функцию Искаков и Плюхин добавили один член – независимую переменную в первой степени. После логарифмирования получен линейный вид:
Пример функции при b0 = 1, b1 = {0,4; 1; 1,5}, b2 = 4 приведен на рис. 4.4. Характер изменения y в начальной ветви кривой до точки максимума функция улавливает автоматически, так как коэффициент b1 получается в процессе решения, а коэффициент b2 определяет скорость этого изменения. В точке b1/b2 находится значение фактора х, при котором результативный признак имеет максимальное значение.
Для решения такой функции в исходной информации нужно вместо y рассчитать ln y, а наряду с х в первой степени ввести ln х. Коэффициент эластичности:
5. Гиперболическая функция применяется в случае, когда размер дополнительного продукта уменьшается с некоторым замедлением (обратная зависимость). График простейшего уравнения гиперболы имеет следующий вид (рис. 4.5). 1. 2. Рис. 4.5. Общий вид уравнения гиперболы
Функция не имеет экстремума, первая производная (отдача фактора) равна:
Коэффициент эластичности равен
Если на предварительном этапе анализа выявлены разные формы связи зависимой переменной с независимыми переменными, то в одном уравнении каждая зависимая переменная представляется в таком виде, который отражает выявленную форму связи. Решение уравнения
Все функции решаются после их линеаризации, то есть после приведения в линейную форму по отношению к переменным. Кривизна зависит от того, в какой форме представлены переменные. Вычисление уравнения регрессии сводится к вычислению его коэффициентов (b0, b1 и т.д.). Основной способ нахождения коэффициентов уравнения – способ наименьших квадратов, (К. Гаусс, 1808 год, немецкий математик). Способ наименьших квадратов состоит в том, что коэффициенты уравнения выбираются так, чтобы сумма квадратов погрешностей (отклонений) была минимальной:
Геометрически погрешности представляют собой разность между ординатой точки на линии регрессии и ординатой точки индивидуального наблюдения, обладающей той же абсциссой. Если нужно определить вклад каждого из фактора в результативный показатель (в случае многофакторного уравнения), то решается уравнение без свободного члена b0. Получится уравнение в β- коэффициентах: у = β1х1 + β2х2 + … βnхn (4.17) где β -коэффициенты – стандартизированные коэффициенты регрессии рассчитываются по формуле:
(4.18)
где bi – значение коэффициента уравнения при факторном признаке; σx – среднеквадратическое отклонение факторного признака; σу – среднеквадратическое отклонение результативного признака. 3. β- коэффициент показывает, что если величина фактора изменится на одно среднеквадратическое отклонение, то зависимая переменная изменится соответственно на β своего квадратического отклонения при постоянстве остальных факторов. Наиболее существенный вклад в вариацию результативного признака обеспечивает тот фактор, для которого значение β- коэффициента наивысшее.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.222.170 (0.01 с.) |

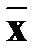 ).
).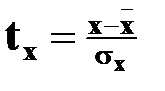 . (4.4)
. (4.4)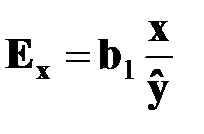 . (4.5)
. (4.5)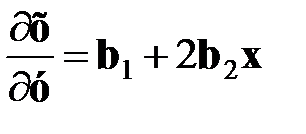 . (4.6)
. (4.6)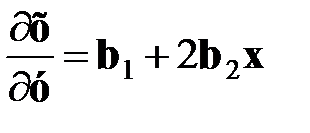 . (4.7)
. (4.7)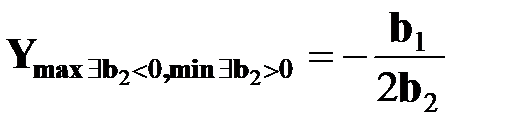 . (4.8)
. (4.8) в литературе называется функцией Кобба-Дугласа по имени американских исследователей, впервые применивших ее в анализе машиностроительного производства.
в литературе называется функцией Кобба-Дугласа по имени американских исследователей, впервые применивших ее в анализе машиностроительного производства.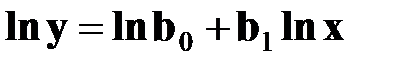 . (4.9)
. (4.9)
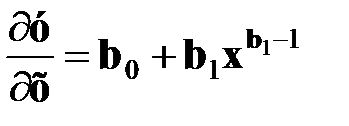 (4.10)
(4.10)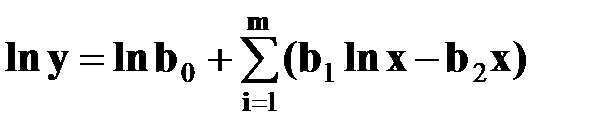 . (4.11)
. (4.11)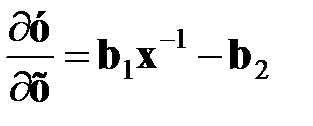 . (4.12)
. (4.12)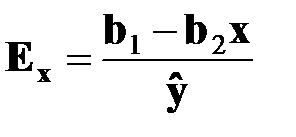 (4.13)
(4.13)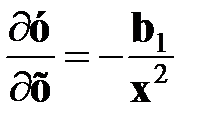 . (4.14)
. (4.14)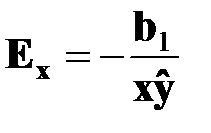 . (4.15)
. (4.15)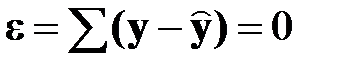 . (4.16)
. (4.16)


