IX. Практическое занятие №1. Расчет электрических цепей с использованием законов Ома и Кирхгофа

1. Вопросы для подготовки к занятиям

1. Сформулировать закон Ома для участка и для замкнутого контура.

2. Нарисовать схемы с последовательным и параллельным соединением пассивных элементов, указать основные свойства этих соединений, схему со смешанным соединением пассивных элементов; дать порядок расчета этих схем.

3. Нарисовать схемы соединения пассивных элементов звездой и треугольником и объяснить порядок их расчета.

4. Сформулировать первый и второй законы Кирхгофа, объяснить правила знаков.

5. Сформулировать уравнение баланса мощностей.

6. Как составляется система уравнений для расчета сложных схем при помощи уравнений Кирхгофа?

Расчет цепи с одним источником питания

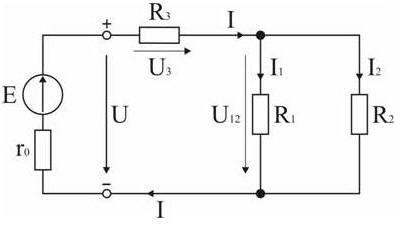
Рисунок 79 к задаче 1.

 

Задача 1. В цепи, схема которой приведена на рис. 79, ЭДС аккумуляторной батареи Е =78 В, ее внутреннее сопротивление r₀ =0,5 Ом. Сопротивления резисторов R ₁=10 Ом, R ₂=5 Ом, R ₃=4 Ом. Вычислить токи во всех ветвях цепи и напряжения на зажимах батареи и на каждом их резисторов.

Анализ и решение задачи 1

1. Обозначение токов и напряжений на участках цепи.

Резистор R ₃ включен последовательно с источником, поэтому ток I для них будет общим, токи в резисторах R ₁ и R ₂ обозначим соответственно I ₁ и I ₂. Аналогично обозначим напряжения на участках цепи.

2. Определение эквивалентного сопротивления цепи:

R _э = r ₀ + R ₃ + R ₁ R ₂ / (R ₁ + R ₂) = 0,5 + 4 + 5 * 10 / (5 +10) = 7,8 Ом

3. Ток в цепи источника рассчитываем по закону Ом а:

I = E / R _э = 78 / 7,8 = 10 А

4. Определение напряжений на участках цепи:

U ₁₂ = R ₁₂ I = 3,3 * 10 = 33 В; U ₃ = R ₃ I = 4 * 10 = 40 В;

U = E - r ₀ I = 78 - 0,5 * 10 = 73 В

5. Определение токов и мощностей всех участков:

I ₁ = U ₁₂ / R ₁ = 33 / 10 = 3,3 А; I ₂ = U ₁₂ / R ₂ = 33 /5 = 6,6 А;

P ₁ = R ₁ I ₁² = U ₁₂ I ₁ = 108,9 Вт; P ₂ = R ₂ I ₂² = U ₁₂ I ₂ = 217,8 Вт;

P ₃ = R ₃ I ² = U ₃ I = 400 Вт.

Мощность потерь на внутреннем сопротивлении источника:

DP = r ₀ I ² = 50 Вт.

Мощность источника:

P = E I = 780 Вт.

2.2. Дополнительные вопросы к задаче 1.

1. Как проверить правильность решения задачи?

Правильность вычисления токов можно проверить, составив уравнение на основании первого закона Кирхгофа: I = I ₁+ I ₂.

Правильность расчета мощностей проверяют по уравнению баланса мощностей: P = P ₁+ P ₂+ P ₃+ DP.

2. Каким будет напряжение на зажимах источника, при обрыве в цепи резистора R ₃?

Это будет режим холостого хода источника ЭДС, при котором U = E, т.к. ток I равен 0 и Ir ₀=0.

3. Каким будет ток в цепи источника при коротком замыкании на его зажимах?

В режиме короткого замыкания U =0 и ток источника ограничивается только его внутренним сопротивлением

I _кз = E / r ₀ = 78 / 0,5 = 156 А

4. Как изменятся токи в схеме при увеличении R ₁?

При увеличении R ₁ увеличивается сопротивление параллельного участка схемы R ₁₂, поэтому увеличивается сопротивление R _экв, что приводит к уменьшению тока I. При уменьшении I уменьшаются падения напряжения IR ₃ и Ir ₀ и, в соответствии со вторым законом Кирхгофа, напряжение на разветвлении U ₁₂= E - I (R ₃+ r ₀) возрастает, что приводит к увеличению тока в резисторе R ₂. Т.к. ток I уменьшается, а ток I ₂ возрастает, ток I ₁= I - I ₂ уменьшается.

Расчет сложных цепей при помощи уравнений Кирхгофа

Задача 2. Рассчитать схему рис. 80, составив систему уравнений на основании законов Кирхгофа.

 

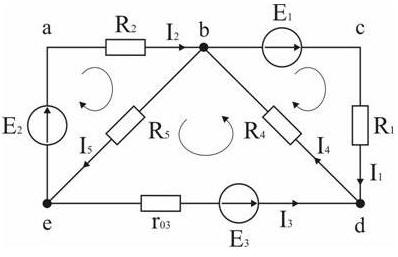
Рисунок 80 к задаче 2.

Исходные данные к задаче:

E ₁ = 60 В; E ₂ = 80 В;      E ₃ = 70 В;

R ₁ = 20 Ом;    R ₂ = 50 Ом;   r ₀₃ = 5 Ом;

R ₄ = 65 Ом;    R ₅ = 85 Ом.

Анализ и решение задачи 2

1. Определение необходимого числа уравнений.

В схеме рис.80 пять ветвей и для расчета токов в них надо составить пять уравнений. По первому закону Кирхгофа составляются уравнения для всех узлов, кроме одного (уравнение для него будет следствием предыдущих), по второму – для независимых контуров (в каждый последующий контур входит хотя бы одна ветвь, не вошедшая в ранее рассмотренные). Для данной схемы надо составить два уравнения по первому закону и три – по второму.

2. Составление и решение системы уравнений.

Для составления уравнений задаемся произвольно направлениями токов в ветвях и направлениями обхода контуров (рис. 80).

Уравнение для узла d:     I ₁ + I ₃ - I ₄ = 0.

Уравнение для узла е:      - I ₂ - I ₃ + I ₅ = 0.

Уравнение для контура bcd:     I ₁ R ₁ + I ₄ R ₄ = E ₁.

Уравнение для контура abe:     I ₂ R ₂ + I ₅ R ₅ = E ₂.

Уравнение для контура bde: I ₃ r ₀₃ + I ₄ R ₄ + I ₅ R ₅ = E ₃.

Подставив в уравнения численные значения величин, получим алгебраическую систему уравнений:

I ₁ + I ₃ - I ₄ = 0;

- I ₂ - I ₃ + I ₅ = 0;

20 I ₁ + 65 I ₄ = 60;

50 I ₂ + 85 I ₅ = 80;

5 I ₃ + 65 I ₄ + 85 I ₅ = 70.

Решение системы дает значения токов:

I ₁=1,093 А; I ₂=0,911 А; I ₃= –0,506 А;  I ₄=0,587 А; I ₅=0,405 А.

3.2. Дополнительные вопросы к задаче 2

1.Что означает минус перед численным значением тока I ₃?

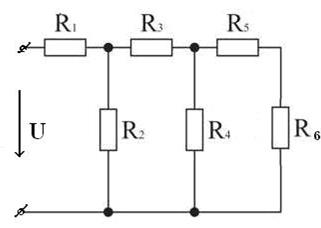
Знак «–» говорит о том, что реальное направление тока в данной ветви противоположно принятому в начале расчета.

2.В каких режимах работают элементы схемы, содержащие источники ЭДС?

В ветвях с E ₁ и E ₂ токи совпадают по направлению с ЭДС, т.е. данные элементы работают источниками, отдавая энергию в схему; в ветви с ЭДС E ₃ ток направлен против ЭДС, т.е. данный элемент работает потребителем (например, машина постоянного тока в режиме двигателя).

3.Как проверить правильность решения задачи?

Для проверки правильности расчета можно на основании законов Кирхгофа написать уравнения для узлов и контуров схемы, которые не использовались при составлении исходной системы. Независимой проверкой является уравнение баланса мощностей: сумма мощностей источников равна сумме мощностей, расходуемых в резистивных элементах схемы. Т.к. элемент схемы с ЭДС может работать как в режиме источника, так и в режиме потребителя, соответствующее слагаемое в левой части уравнения берется с плюсом, если Е и I совпадают по направлению (источник), и с минусом, если направления противоположны (потребитель).

Мощности элементов схемы с ЭДС:

E ₁ I ₁+ E ₂ I ₂ - E ₃ I ₃ = 60 * 1 * 1,093 + 80 * 0,911 - 70 * 0,506 = 104,04 Вт.

Мощности, расходуемые в резистивных элементах схемы:

I ₁² R ₁ + I ₂² R ₂ + I ₃² r ₀₃ + I ₄² R ₄+ I ₅² R ₅ = 1,093² * 20 + 0,911² * 50 + 0,506² * 5 + 0,587² * 65 + 0,405² * 85 = 103,01 Вт.

ΣEI=ΣP.

Баланс мощностей сошелся, следовательно, задача решена верно.

4. Самостоятельная работа студента

Задача 1. Две лампы, имеющие одинаковые номинальные напряжения 110 В и номинальные мощности Р_{1н ом}=50 Вт и Р_{2н ом}=150 Вт, соединены последовательно и включены в сеть с напряжением U =220 В. Определить напряжения на лампах и мощности, потребляемые каждой лампой, если допустить, что сопротивление ламп не зависит от тока.

Задача 2. Цепь постоянного тока содержит несколько резисторов, соединенных смешанно рис. 81. Индекс тока или напряжения совпадает с индексом резистора, по которому проходит этот ток или на который действует это напряжение. Начертить схему цепи, указать действительные направления токов, проходящих по всем сопротивлениям цепи и определить следующие величины, относящиеся к данной цепи, если они не заданы в условии задачи:

·  эквивалентное сопротивление цепи;

·  напряжение U, приложенное к цепи;

·  ток I на входе цепи;

·  токи, проходящие по всем резисторам;

·  мощность Р, потребляемую всей цепью.

Дано: R 1 = 8 Ом, R 2 = 6 Ом, R 3 = 4 Ом, R 4 = 2 Ом, R 5 = 4 Ом, R 6 = 2 Ом, I 2 = 2 А

Рисунок 81 к задаче для самостоятельной работы

Задача 3. Для электрической цепи рис. 82 определить:

· Токи в ветвях методом преобразований (схему упрощают путем замены участков с параллельным или последовательным соединением эквивалентными элементами).

· Мощность, развиваемую источником энергии и мощность потребителей. Проверить баланс мощности.

· Составить уравнения по первому закону Кирхгофа для узлов схемы. Составить уравнение по второму закону Кирхгофа для любого замкнутого контура, включающего ЭДС Е.

 Дано: E = 60 B; R ₁ = 6 Oм; R ₂ = 11 Ом; R ₃ = 7 Ом; R ₄ = 12 Ом; R ₅ = 8 Ом; R ₆ = 13 Ом.

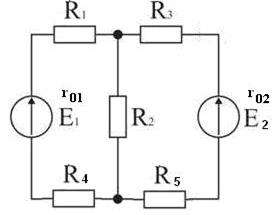
Рисунок 82 к задаче для самостоятельной работы

Задача 4. Для электрической цепи, изображенной на рисунке 83, по заданным ЭДС источников постоянного тока (Е) и сопротивлениям ветвей выполнить следующее:

· Определить токи во всех ветвях.

· Определить суммарную мощность, потребляемую цепью.

· Ооставить уравнение баланса мощностей между источниками и приемниками электроэнергии.

Задачу решить способом  контурных токов.

Дано: R ₁ = 4 Oм, R ₂ = 3 Oм, R ₃ = 15 Oм, R ₄ = 8 Oм, R ₅ = 4 Oм, Е₁ = 65 В, r₀₁ = 0,15 Ом, Е₂ = 50 В, r₀₂ = 0,1 Ом.

Рисунок 83 к задаче для самостоятельной работы