
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соединение фаз приемника по схеме «треугольник»Содержание книги
Поиск на нашем сайте
Кроме соединения в звезду широкое применение получили трехпроводные трехфазные цепи с соединением приемников в треугольник. Если три фазы приемника с фазными сопротивлениями
Рисунок 143.Соединение фаз приемника по схеме «треугольник»
Из схемы видно, что если пренебречь сопротивлениями линейных проводов, то независимо от характера нагрузки напряжение на каждой фазе приемника равно линейному напряжению:
Но фазные и линейные токи (в отличие от схемы соединения в звезду) не равны между собой. За положительное направление фазных токов I а b, Ib с, I са принято направление от начала к концу фазы. Если напряжения и сопротивления фаз нагрузки заданы, то фазные токи определяются по формулам:
Угол сдвига фаз между фазными токами и напряжениями определяется характером нагрузки и в общем случае может быть вычислен по формулам
где: Raв, Rвc, Rca - активные сопротивления фаз приемника. Линейные токи определяются по фазным токам из уравнений, составленных по первому закону Кирхгофа для узлов а, в, с:
Из уравнений (9) следует, что любой из линейных токов равен геометрической разности токов тех двух фаз нагрузки, которые соединяются с данным линейным проводом, а также следует, что независимо от характера нагрузки геометрическая сумма линейных токов в трехпроводной цепи равна нулю.
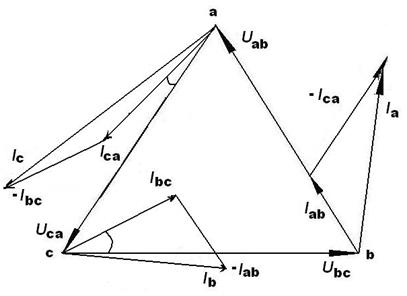
Рассмотрим пример расчета трехфазной цепи при соединении фаз приемника по схеме треугольник для случая, когда Zab > Zbc > Zca . (16.10) φ ab =0, φ bc <0, φ ca >0. Согласно (16.7) между фазными токами будет справедливо следующее соотношение: Iab > Ibc > Ica . Так как φа b = 0, поэтому нагрузка в фазе " а b " будет носить чисто активный характер. В фазе " b с " φ bc < 0 и нагрузка имеет активно-индуктивный характер. В фазе " са " φ ca > 0 инагрузка имеет активно-емкостный характер. На рис. 144. построена векторная диаграмма линейных напряжений и фазных и линейных токов для данного случая.
Рисунок 144. Векторные диаграммы токов и напряжений при разнородной несимметричной нагрузке: Zab > Zbc > Zca , φ ab =0, φ bc <0, φ ca >0
Построение векторной диаграммы токов производилось в следующем порядке: 1. Из точки " b " векторной диаграммы линейных напряжений строим вектор тока I ав совпадающим с напряжением Uae (φав = 0). 2. Из точки " с " строим вектор тока Ib с под углом φ b с к вектору напряжения U b c. Угол φ b с откладывается против часовой стрелки, т. к. при активно-емкостной нагрузке ток опережает напряжение. 3. Из точки " а " строим вектор тока I са под углом φса к вектору напряжения Uca. Угол φса откладываем по часовой стрелке, т. к. при активно-индуктивной нагрузке ток отстает от напряжения. Согласно (16.9) строим вектора линейных токов в следующем порядке: 1. Из конца вектора I а b строим вектор - I са, параллельно вектору I са, но имеющему обратное направление. Вектор тока I а строится из начала вектора I а b в конец вектора - I са. 2. Из конца вектора Ibc строим вектор - I а b, параллельно вектору I а b, но имеющему обратное направление. Вектор тока I в строится из начала вектора Ib с в конец вектора - I ав. 3. Из конца вектора I са строим вектор I вс, параллельно вектору 1вс, но имеющему обратное направление. Вектор тока I с строится из начала вектора I са в конец вектора - Ibc. Мощность трехфазной цепи В трехфазных цепях, так же как и в однофазных, пользуются понятиями активной, реактивной и полной мощностей. Но в цепях однофазного тока мгновенная мощность является функцией времени и изменяется с двойной частотой. Мгновенная мощность симметричной трёхфазной цепи остаётся неизменной во времени. Активная мощность трехфазной цепи равна сумме активных мощностей всех фаз, в частности: · для схемы звезда:
где: · для схемы треугольник:
где: Реактивная мощность трехфазной цепи равна алгебраической сумме реактивных мощностей всех фаз, в частности: · для схемы звезда:
где: · для схемы треугольник:
где Полная мощность трехфазной цепи равна геометрической сумме активной и реактивной мощностей:
Для симметричной трехфазной цепи активная мощность равна:
При расчетах трехфазной цепи удобно пользоваться линейными значениями напряжений и токов. Так, если при соединении по схеме «звезда»:
а при соединении по схеме «треугольник»:
то независимо от схемы соединения фаз приемника активная мощность потребления энергии симметричной трехфазной цепи:
Аналогично определяются реактивная и полная мощности симметричной трехфазной цепи:
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 78; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.219 (0.01 с.) |

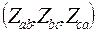 включить непосредственно между линейными проводами трехпроводной цепи, то получим соединение приемников в треугольник (рис. 143).
включить непосредственно между линейными проводами трехпроводной цепи, то получим соединение приемников в треугольник (рис. 143).
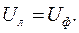 .
.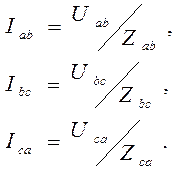 (16.7)
(16.7) , (16.8)
, (16.8)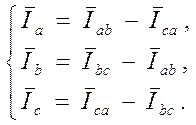 (16.9)
(16.9)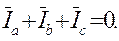
 , (16.11)
, (16.11)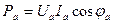 - активная мощность фазы «а»,
- активная мощность фазы «а»,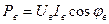 - активная мощность фазы «в»,
- активная мощность фазы «в»,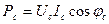 - активная мощность фазы «с»;
- активная мощность фазы «с»;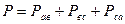 , (16.12)
, (16.12) - активная мощность фазы «ав»,
- активная мощность фазы «ав»,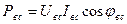 - активная мощность фазы «вс»,
- активная мощность фазы «вс», - активная мощность фазы «са».
- активная мощность фазы «са».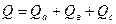 , (16.13)
, (16.13) - реактивная мощность фазы «а»,
- реактивная мощность фазы «а»,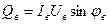 - реактивная мощность фазы «в»,
- реактивная мощность фазы «в»,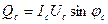 - реактивная мощность фазы «с»,
- реактивная мощность фазы «с»,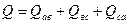 , (16.14)
, (16.14) - реактивная мощность фазы «ав»,
- реактивная мощность фазы «ав»,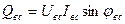 - реактивная мощность фазы «вс»,
- реактивная мощность фазы «вс»,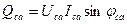 - реактивная мощность фазы «са».
- реактивная мощность фазы «са».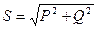 (16.15)
(16.15) (16.16)
(16.16)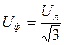 ,
,  ,
, ,
,  ,
,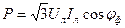 (16.17)
(16.17)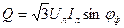 ; (16.18)
; (16.18)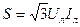 . (16.19)
. (16.19)


