
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
XII. Практическое занятие №4. Расчет сложных цепей переменного токаСодержание книги
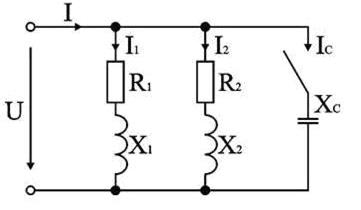
Поиск на нашем сайте 1. Вопросы для подготовки к занятиям 1. Как рассчитать ток, потребляемый из сети, при параллельном соединении резистора, индуктивной катушки и конденсатора, если параметры потребителей и приложенное напряжение известны? 2. Как рассчитать активную и реактивную составляющие тока отдельной ветви и общего тока, если известны параметры параллельно включенных потребителей и приложенное напряжение? 3. Построить векторные диаграммы токов и напряжений для цепей, содержащих параллельное соединение R и L, R и C, реальной катушки (с активным сопротивлением R и индуктивностью L) и C. 4. Что такое коэффициент мощности потребителя? Объяснить экономическое значение коэффициента мощности. 5. Как рассчитать коэффициент мощности цепи, если известны параметры параллельно включенных потребителей энергии? 6. Как рассчитать активную, реактивную и полную мощности цепи при параллельном соединении потребителей, параметры которых известны? 7. Как повысить коэффициент мощности цепи? 8. С какой целью повышают коэффициент мощности цепи? 9. Как рассчитать необходимую емкость конденсатора, включенного для полной компенсации реактивной энергии? 10. Как должен изменяться потребляемый из сети ток при повышении коэффициента мощности цепи? 11. Изменится ли ток в цепи потребителя, если к нему параллельно подключить конденсатор? 12. Как изменится потребляемая из сети активная мощность при подключении параллельно индуктивной катушке: а) резистора, б) конденсатора? 13. Каковы принципы расчета цепей переменного тока комплексным методом? Расчет цепи с параллельным соединением элементов Задача 1. К источнику с напряжением 220 В и частотой 50 Гц подключены параллельно два двигателя, активные мощности и коэффициенты мощности которых P 1=0,3 кВт, P 2=0,4 кВт, cosφ 1=0,6, cosφ 2=0,7. Начертить электрическую схему замещения цепи. Определить токи каждого двигателя и ток, потребляемый схемой от источника, ее активную, реактивную и полную мощности. Для повышения cos φ цепи до 0,9 подключить параллельно нагрузке конденсатор и определить его емкость, рассчитать ток, потребляемый схемой от источника в этом режиме. Построить в масштабе векторную диаграмму напряжения и токов. Анализ и решение задачи 1 1.Схема замещения каждого двигателя может быть представлена в виде последовательного соединения резистивного и индуктивного элементов, т.к. в двигателе происходит как необратимое преобразование электрической энергии в механическую и тепловую энергию, так и колебательный обмен энергией между магнитным полем двигателя и сетью. Схема замещения к задаче представлена на рис. 99.
Рисунок 99 к задаче 1
2.Токи двигателей рассчитываются по паспортным данным:
Сдвиги токов по фазе по отношению к напряжению: φ1 =53,1°, φ 2=45,5°. 3. Мощности ветвей приведены в исходных данных, поэтому расчет схемы удобно вести через треугольники мощностей. Реактивные мощности двигателей: Q 1 = U I 1 sin φ1 = 220 · 2,27 · 0,8 = 399 ВАр; Q 2 = U I 2 sin φ2 = 220 · 2,6 · 0,713 = 407 ВАр. Активная и полная мощности всей цепи: P = P 1 + P 2 = 300 + 400 = 700 Вт; Q = Q 1 + Q 2 = 399 + 407 = 806 ВАр;
Ток в цепи источника: I = S / U = 1068 / 220 = 4,85 А.. Коэффициент мощности схемы: cos φ = P / S = 700 / 1068 = 0,655. 4. Рассчитаем емкость конденсатора, необходимую для повышения коэффициента мощности схемы до cos φ'=0,9. Включение конденсатора параллельно нагрузке не изменяет ее активную мощность, а уменьшает реактивную и полную мощности, потребляемые всей схемой от источника. Поэтому по активной мощности цепи и заданному значению cos φ' определим полную мощность цепи: S ' = P / cos φ' = 700 / 0,9 = 777,8 В A. Реактивная мощность цепи:
Реактивная мощность всей цепи равна алгебраической сумме реактивных мощностей ее участков. В данном случае Q '= Q - QC, поэтому мощность конденсатора: QC = Q - Q ' = 806 - 339= 467 ВАр. Многоугольник мощностей показан на рис. 100.
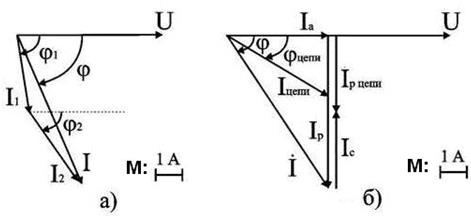
Рисунок 100 к задаче 1 Ток в цепи конденсатора и его сопротивление: IC = QC / U = 467 / 220 = 2,12 А;XC = U / IC = 220 / 2,12 = 103 Ом. Емкость конденсатора: C = 1 / (2π f XC) = 1 / (2π · 50 · 103) = 30,7·10-6 Ф = 30,7 мкФ. Результирующий ток источника: I ' = S ' / U = 777,8 / 220 = 3,535 A. На рис. 101 приведены векторные диаграммы напряжения и токов схемы без конденсатора (а) и после подключения параллельно нагрузке конденсатора (б).
Рисунок 101 к задаче 1
5.Если в исходных данных приведены сопротивления ветвей или их токи и коэффициенты мощности, то расчет удобно вести через треугольники токов (их активные и реактивные составляющие). Активные составляющие токов ветвей: I 1а = I 1 cos φ1 = 2,27 · 0,6 = 1,362 А; I 2а = I 2 cos φ2 = 2,6 · 0,7 = 1,818 А; I а = I 1а + I 2а = 1,362 · 1,818 = 3,18 A. Реактивные составляющие токов ветвей: I 1р = I 1 sinn φ1 = 2,27 · 0,8 = 1,818 А; I 2р = I 2 sinn φ2 = 2,6 · 0,713 = 1,852 А; I р = I 1р + I 2р = 1,818 · 1,852 = 3,67 A. Полный ток источника:
Коэффициент мощности эквивалентной нагрузки: cos φ = I а / I = 3,18 / 4,854 = 0,655. Реактивная составляющая тока источника после подключения конденсатора: I 'р = I а t g φ' = 3,18 · 0,484 = 1,54 A. Ток конденсатора: IC = I р - I 'р = 3,67 - 1,54 = 2,13 A. Далее определяются XC и С, как было рассмотрено выше. 2.2. Дополнительные вопросы к задаче 1 1. Как по результатам расчета определить параметры последовательной схемы замещения двигателей и всей схемы в целом? Полные сопротивления двигателей определяются по закону Ома: Z 1 = U / I 1; Z 2 = U / I 2. Активные и реактивные составляющие сопротивлений рассчитываются через треугольники сопротивлений: R1 = Z1 cos φ1; R2 = Z2 cos φ2; X1 = Z1 sinn φ1; X2 = Z2 sinn φ2. Сопротивления можно подсчитать также и через треугольники мощностей. Например, для схемы в целом: R = P / I 2 = 700 / 4,8562 = 29,68 Ом; X = Q / I 2 = 339 / 4,8562 = 14,37 Ом. 2. Какова схема замещения цепи при представлении токов ветвей в виде суммы активных и реактивных составляющих. Разложение тока на составляющие соответствует представлению реального элемента цепи в виде соединенных параллельно идеальных активного и реактивного сопротивлений (рис. 102). Параметры схемы подсчитываются по закону Ом а или через мощности: R ' = U / I а = U 2 / P; X ' = U / I р = U 2 / Q; Z = U / I = U 2 / S.
Рисунок 102 Рис. 6.14.
3. Как изменятся токи в схеме, если параллельно двигателю подключить осветительную (чисто активную) нагрузку? За счет увеличения активной составляющей (освещение) ток источника возрастет, токи в ветвях схемы не изменятся. 4. Как рассчитать схему графоаналитическим методом? Для определения тока источника рассчитываются, как это было приведено выше, токи в ветвях I 1 и I 2 и их сдвиги по фазе φ1 и φ2 по отношению к напряжению. Далее строится в масштабе векторная диаграмма токов и по диаграмме определяется величина тока I и его сдвиг по фазе по отношению к напряжению φ (рис. 101). 5. Как рассчитать токи в схеме комплексным методом? Для расчета связываем векторную диаграмму с комплексной плоскостью; для упрощения выкладок один из векторов, например, напряжение, направим по действительной оси, т.е. U =220 B. Токи в ветвях в комплексной форме: Í1 = 2,27 e - j 53,1° = 2,27 (cos 53,1° - j sin 53,1°) = (1,36 - j 1,81) А; Í2 = 2,6 e - j 45,5° = 2,6 (cos 45,5° - j sin 45,5°) = (1,82 - j 1,84) По первому закону Кирхгофа ток источника: Í = Í1 + Í2 = 1,36 - j 1,81 + 1,82 - j 1,84 = 3,18 - j 3,66 = 4,85 e - j 49° Мощность цепи в комплексной форме: S = Ú Î = 220 · 4,85 ej 49° =1067 ej 49° = (700 + j 806) ВА; S =1067 ВА; P =700 Вт; Q =806 ВАр. Батарея конденсаторов рассчитывается, как это было рассмотрено выше.
|
||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 208; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

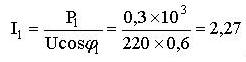 А;
А; 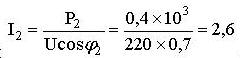 А.
А.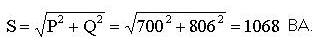 В
В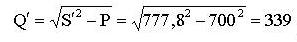 ВАр.
ВАр.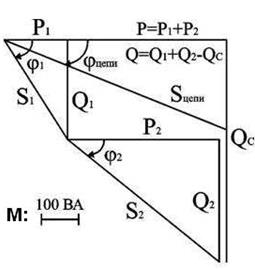
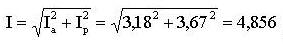 A.
A.



