Расчет цепи методом комплексных чисел

Запишем в комплексном виде сопротивление каждого элемента и всей цепи:

R = 4 e^{j 0°} = 4 Ом;

X_L =8 e ^{+ j 90°} = j 8 Ом;  X_C =5 e ^{- j 90°} = - j 5 Ом.

Z = R + j (X_L - X_C) = 4 + j (8 - 5) Ом.

На комплексной плоскости в масштабе: в 1 см – 2 Ом, построим треугольник сопротивлений (рис. 94. а).

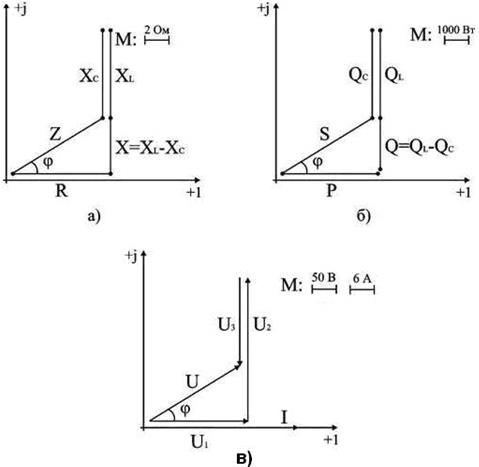
Рисунок 94 к задаче 1

 

Из треугольника определим величину полного сопротивления Z и угол фазового сдвига φ:

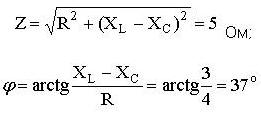
В показательной форме полное сопротивление всей цепи запишется в виде:

Z = Ze ^{+ j φ} = 5 e ^{+ j 37°} Ом.

Примем начальную фазу приложенного к цепи напряжения за нуль и определим по закону Ом а ток в данной цепи

Í = Ú / Z = 120 e ^{+ j 0°} / 5 e ^{+ j 37°}

Следовательно, в данной цепи ток отстает по фазе от напряжения на угол φ. Зная величину тока I, определим мощности для отдельных элементов и всей цепи:

P = 2304 Вт;  Q_L =4608 ВАр; Q_C =2880 ВАр.

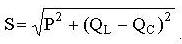
Треугольник мощностей в масштабе: в 1 см – 1000 Вт (ВАр); (ВА), построим (рис. 94. б) на основе выражения для полной мощности:

S ² = P ² + (Q_L - Q_C)².

Для построения векторных диаграмм по току и напряжениям примем начальную фазу тока равной нулю, т.к. ток I в данной схеме является одним и тем же для всех элементов в цепи:

Í = Ie ^{+ j 0°} / 24 e ^{+ j 0°}.

Запишем выражения для напряжений в комплексной форме:

Ú₁ = R Í = 96 e ^{+ j 0°} В;     Ú₂ = X_L Í = 192 e ^{+ j 90°} В;

Ú₃ = X_C Í = 120 e ^{- j 90°} В;     Ú = Z Í = 120 e ^{+ j 37°}.

Выберем масштабы для векторной диаграммы: в 1 см – 6 А; в 1 см – 50 B. Векторная диаграмма напряжений строится на основе второго закона Кирхгофа для данной цепи:

Ú = Ú₁ + Ú₂ + Ú₃.

Векторная диаграмма цепи показана на рис. 94 в. При последовательном соединении элементов построение диаграммы начинают с вектора тока Í, по отношению к которому ориентируются вектора напряжений на участках цепи: напряжение на активном сопротивлении Ú₁ совпадает с ним по направлению, напряжение на индуктивности Ú₂ опережает его на 90°, на емкости отстает на 90°. Полное напряжение Ú строится как их векторная сумма.

 

 3.1. Дополнительные вопросы к задаче 1

1. Какой характер носит эквивалентное реактивное сопротивление цепи?

По условию задачи X_L > X_C, поэтому X = X_L - X_C имеет индуктивный характер. Обратите внимание, что реактивные сопротивления отдельных участков цепи (X_L, X_C) могут быть больше ее полного сопротивления, так в данном случае X_L > Z.

2. Как изменяется режим работы цепи при изменении частоты питающего напряжения?

От частоты зависят реактивные сопротивления: X_L прямо пропорционально частоте f, X_C обратно пропорционально f. В рассматриваемой схеме X_L > X_C, поэтому при росте частоты X возрастает, ток уменьшается и возрастает угол φ его отставания от напряжения. При уменьшении частоты X уменьшается и при некотором ее значении X =0, т.е. схема ведет себя как чисто активное сопротивление (режим резонанса напряжений, при котором U_L = U_C, Z = R и ток наибольший). При дальнейшем уменьшении частоты X_C > X_L, Z возрастает, I уменьшается, схема ведет себя как активно-емкостное сопротивление.