Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет цепи синусоидального тока со смешанным соединением элементовСодержание книги
Поиск на нашем сайте 2.1 Содержание домашнего задания В домашнем задании предусматривается расчет электрической цепи со смешанным соединением элементов, состоящей из двух параллельных ветвей, в каждой из которых последовательно включено не менее двух элементов. В домашнем задании необходимо: 1. По исходной схеме (рис. 135) нарисовать электрическую схему согласно заданному варианту (табл. 15.1). Элементы, сопротивления которых равны нулю, исключаются из схемы.
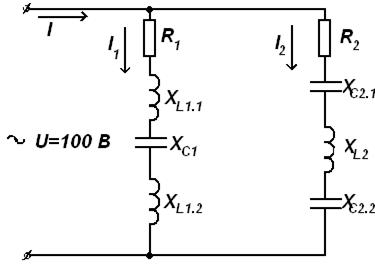
Рисунок 135. Исходная электрическая схема 2. Методом проводимостей рассчитать токи в параллельных ветвях и неразветвленной части цепи. 3. Вычислить активную, реактивную и полную мощности параллельных ветвей и всей цепи. 4. Построить векторную диаграмму токов и напряжений. 5. Изменяя одно из реактивных сопротивлений параллельной ветви, добиться, чтобы схема работала в режиме резонанса токов. Если в заданной цепи резонанс токов невозможен, ввести в одну из параллельных ветвей дополнительное реактивное сопротивление (индуктивность или емкость). 6. Построить векторную диаграмму токов и напряжений при работе цепи в резонансе токов. 7. При расчетах считать напряжение, приложенное к цепи, равным U =100 (В), сопротивления элементов заданы в табл. 15.1. Пример расчета электрической цепи со смешанным соединением элементов Рассмотрим порядок расчета электрической цепи соответствующей варианту 72. Дано: R 1 =0 Ом, R 2 =20 Ом, XL 1.1 =10 Ом, XC 2.1 =0, XC 1 =40 Ом, XL 2 =20 Ом, XL 1.2 =0 Ом, XC 2.2 =0 Ом.. Данному варианту соответствует электрическая схема рис. 136.
Рисунок 136. Электрическая схема цепи, согласно варианту 3
Расчет производится в следующем порядке: 1. Определяем полное сопротивление первой ветви:
2. Определяем полное сопротивление второй ветви:
Примечание: расчет вести до четырех значащих цифр. 3. Определяем активную проводимость первой ветви:
4. Определяем реактивную проводимость первой ветви:
5. Определяем полную проводимость первой ветви:
6. Определяем активную составляющую первого тока:
7. Определяем реактивную составляющую первого тока:
8. Определяем полный ток первой ветви:
9. Определяем активную проводимость второй ветви:
10. Определяем реактивную проводимость второй ветви:
11. Определяем полную проводимость второй ветви:
12. Определяем активную составляющую тока второй ветви:
13. Определяем реактивную составляющую тока второй ветви:
14. Определяем полный ток второй ветви:
15. Определяем активную проводимость всей цепи:
16. Определяем реактивную проводимость всей цепи:
17. Определяем полную проводимость всей цепи:
18. Определяем активную составляющую тока в неразветвленной части цепи:
19. Определяем реактивную составляющую тока в неразветвленной части цепи:
20. Определяем полный ток в неразветвленной части цепи:
21. Определяем коэффициент мощности первой ветви:
22. Определяем коэффициент мощности второй ветви:
23. Определяем коэффициент мощности всей цепи:
24. Определяем полную мощность первой ветви:
25. Определяем активную мощность первой ветви:
26. Определяем реактивную мощность первой ветви:
27. Определяем полную мощность второй ветви:
28. Определяем активную мощность второй ветви:
29. Определяем реактивную мощность второй ветви:
30. Определяем полную мощность всей цепи:
31. Определяем активную мощность всей цепи:
32. Определяем реактивную мощность всей цепи:
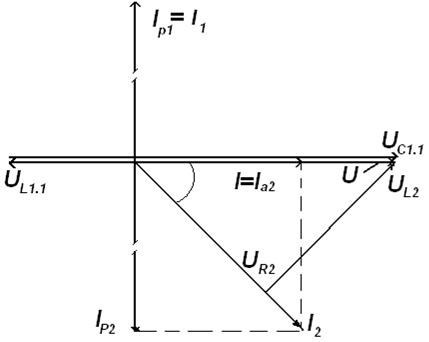
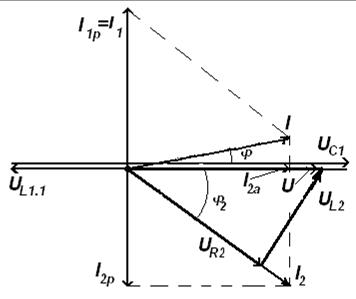
33. Векторная диаграмма токов (рис 137)строится на основании первого закона Кирхгофа для цепей синусоидального тока:
Векторная диаграмма токов строится в следующем порядке: 33.1 За базовую ось принимаем вектор напряжения U, который является общим для обеих параллельных ветвей. Строим этот вектор горизонтально в масштабе mU. 33.2 По активной и реактивной составляющей первого тока строится вектор тока I 1. Но так как активная составляющая первого тока I 1 a =0, то полный ток I 1 будет равенреактивной составляющей I 1р, которая имеет емкостный характер и опережает вектор напряжения U на угол 90° (X = XL 1.1 – XC 1 <0). Этот вектор строим перпендикулярно к вектору напряжения U против часовой стрелки (φ1=-90°) в масштабе m 1. 33.3 Аналогично строим вектор тока второй ветви. Активная составляющая тока I 2 a совпадает по фазе с вектором напряжения U, реактивная составляющая тока второй ветви I 2р носит индуктивный характер (X 2 = XL 2 >0) и отстает от вектора напряжения U на угол 90°. Этот вектор строим перпендикулярно к вектору напряжения по часовой стрелке. Вектор полного тока второй ветви будет равен диагонали параллелограмма построенного на векторах I 2 a и I 2р. 34. Векторная диаграмма напряжений для первой ветви строится на основании второго закона Кирхгофа:
Рисунок 137. Векторная диаграмма токов и напряжений Векторная диаграмма напряжений строится в следующем порядке: 34.1 Строится вектор падения напряжения на индуктивном сопротивлении XL 1.1, модуль которого равен:
На индуктивности напряжение опережает ток на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I 1 против часовой стрелки. 34.2 Из конца вектора UL 1.1 строится вектор падения напряжения на емкостном сопротивлении XC 1, модуль которого равен:
На емкости напряжение отстает от тока на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I 1 по часовой стрелке. Если вычисления и построения сделаны верно, то конец вектора UC 1 будет совпадать с концом вектора U. 35. Векторная диаграмма напряжений для второй ветви строится на основании второго закона Кирхгофа:
Векторная диаграмма напряжений для второй ветви строится в следующем порядке: 35.1 Строится вектор падения напряжения на активном сопротивлении R 2, модуль которого равен
На активном сопротивлении напряжение и ток совпадают по фазе, поэтому этот вектор падения напряжения строим совпадающим по направлению с вектором тока I 2. 35.2 Из конца вектора UR 2 строится вектор падения напряжения на индуктивном сопротивлении XL 2, модуль которого равен:
Напряжение на индуктивности опережает ток на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I 2 против часовой стрелки. Если вычисления и построения сделаны верно, конец вектора напряжения UL 2 будет совпадать с концом вектора U. Рекомендуемый масштаб: mu =1 B /мм, mI =0,05А/мм. 36. Для обеспечения резонанса токов в электрической схеме с двумя параллельными ветвями должны выполняться следующие условия: · параллельные ветви должны иметь разный характер проводимостей (одна индуктивный, другая емкостный). · реактивные проводимости параллельных ветвей должны быть равны по модулю, т.е.:
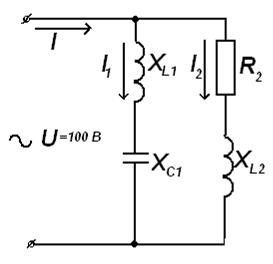
В данном варианте первое условие выполняется, т.к. первая ветвь носит емкостный, а вторая – активно-индуктивный характер. Для достижения резонанса токов, т.к.
37. После включения дополнительной емкости в первую ветвь изменится ток в этой ветви и падения напряжения на индуктивности и емкости.
Векторная диаграмма, построенная аналогично п.п. 33-35, представлена на рис. 138. Рекомендуемый масштаб: mu =1 B /мм, mI =0,05А/мм.
Рисунок 138. Векторная диаграмма токов и напряжений для случая резонанса токов
Таблица15.1
Величина сопротивления (Ом) | ||||||||||||||
| R1 | XL1.1 | XC1 | XL1.2 | R2 | XC2.1 | XL2 | XC2.2 | ||||||||
| 1 | 0 | 0 | 40 | 20 | 20 | 30 | 0 | 10 | |||||||
| 2 | 0 | 10 | 0 | 20 | 20 | 0 | 20 | 10 | |||||||
| 3 | 0 | 10 | 40 |
20 | 20 | 0 | 10 | 20 | |||||||
| 4 | 0 | 10 | 40 | 20 | 20 | 0 | 0 | 10 | |||||||
| 5 | 10 | 0 | 0 | 20 | 0 | 30 | 20 | 10 | |||||||
| 6 | 10 | 0 | 40 | 0 | 0 | 30 | 20 | 0 | |||||||
| 7 | 10 | 0 | 40 | 20 | 0 | 30 | 0 | 10 | |||||||
| 8 | 10 | 10 | 0 | 20 | 0 | 0 | 20 | 10 | |||||||
| 9 | 0 | 0 | 40 | 20 | 20 | 30 | 20 | 0 | |||||||
| 10 | 0 | 10 | 0 | 20 | 20 | 30 | 0 | 0 | |||||||
| 11 | 0 | 10 | 40 | 0 | 20 | 0 | 20 | 10 | |||||||
| 12 | 0 | 10 | 40 | 20 | 20 | 0 | 20 | 0 | |||||||
| 13 | 10 | 0 | 40 | 0 | 0 | 30 | 20 | 10 | |||||||
| 14 | 10 | 0 | 40 | 20 | 0 | 30 | 20 | 0 | |||||||
| 15 | 10 | 10 | 0 | 0 | 0 | 30 | 0 | 10 | |||||||
| 16 | 10 | 10 | 40 | 0 | 0 | 0 | 20 | 10 | |||||||
| 17 | 0 | 10 | 0 | 20 | 20 | 30 | 0 | 10 | |||||||
| 18 | 0 | 10 | 40 | 0 | 20 | 30 | 0 | 0 | |||||||
| 19 | 0 | 10 | 40 | 20 | 20 | 0 | 20 | 10 | |||||||
| 20 | 10 | 0 | 0 | 20 | 20 | 0 | 0 | 10 | |||||||
| 21 | 10 | 0 | 40 | 20 | 0 | 30 | 20 | 10 | |||||||
| 22 | 10 | 10 | 0 | 0 | 0 | 30 | 20 | 0 | |||||||
| 23 | 10 | 10 | 0 | 20 | 0 | 30 | 0 | 10 | |||||||
| 24 | 0 | 10 | 0 | 20 | 20 | 30 | 20 | 0 | |||||||
| 25 | 0 | 10 | 40 | 0 | 20 | 30 | 0 | 10 | |||||||
| 26 | 0 | 10 | 40 | 20 | 20 | 30 | 0 | 0 | |||||||
| 27 | 10 | 0 | 0 | 20 | 20 | 0 | 20 | 0 | |||||||
| 28 | 10 | 0 | 40 | 0 | 20 | 0 | 0 | 10 | |||||||
| № | Величина сопротивления (Ом) | ||||||||||||||
| R1 | XL1.1 | XC1 | XL1.2 | R2 | XC2.1 | XL2 | XC2.2 | ||||||||
| 29 | 10 | 10 | 0 | 0 | 0 | 30 | 20 | 10 | |||||||
| 30 | 10 | 10 | 0 | 20 | 0 | 30 | 20 | 0 | |||||||
| 31 | 10 | 10 | 40 | 0 | 0 | 30 | 0 | 10 | |||||||
| 32 | 0 | 10 | 40 | 0 | 20 | 30 | 20 | 0 | |||||||
| 33 | 0 | 10 | 40 | 20 | 20 | 30 | 0 | 10 | |||||||
| 34 | 10 | 0 | 0 | 20 | 20 | 0 | 20 | 10 | |||||||
| 35 | 10 | 0 | 40 | 0 | 20 | 0 | 20 | 0 | |||||||
| 36 | 10 | 0 | 40 | 20 | 20 | 0 | 0 | 10 | |||||||
| 37 | 10 | 10 | 0 | 20 | 0 | 30 | 20 | 10 | |||||||
| 38 | 10 | 10 | 40 | 0 | 0 | 30 | 20 | 0 | |||||||
| 39 | 0 | 10 | 40 | 20 | 20 | 30 | 20 | 0 | |||||||
| 40 | 10 | 0 | 0 | 20 | 20 | 30 | 0 | 0 | |||||||
| 41 | 10 | 0 | 40 | 0 | 20 | 0 | 20 | 10 | |||||||
| 42 | 10 | 0 | 40 | 20 | 20 | 0 | 20 | 0 | |||||||
| 43 | 10 | 10 | 0 | 0 | 20 | 0 | 0 | 10 | |||||||
| 44 | 10 | 10 | 40 | 0 | 0 | 30 | 20 | 10 | |||||||
| 45 | 0 | 0 | 40 | 20 | 0 | 0 | 20 | 10 | |||||||
| 46 | 10 | 0 | 0 | 20 | 20 | 30 | 0 | 10 | |||||||
| 47 | 10 | 0 | 40 | 0 | 20 | 30 | 0 | 0 | |||||||
| 48 | 10 | 0 | 40 | 20 | 20 | 0 | 20 | 10 | |||||||
| 49 | 10 | 10 | 0 | 0 | 20 | 0 | 20 | 0 | |||||||
| 50 | 10 | 10 | 0 | 20 | 20 | 0 | 0 | 10 | |||||||
| 51 | 10 | 0 | 0 | 20 | 20 | 30 | 20 | 0 | |||||||
| 52 | 10 | 0 | 40 | 0 | 20 | 30 | 0 | 10 | |||||||
| 53 | 10 | 0 | 40 | 20 | 20 | 30 | 0 | 0 | |||||||
| 54 | 10 | 10 | 0 | 0 | 20 | 0 | 20 | 10 | |||||||
| 55 | 10 | 10 | 0 | 20 | 20 | 0 | 20 | 0 | |||||||
| 56 | 10 | 10 | 40 | 0 | 20 | 0 | 0 | 10 | |||||||
| 57 | 0 | 0 | 40 | 20 | 0 | 30 | 0 | 10 | |||||||
| R1 | XL1.1 | XC1 | XL1.2 | R2 | XC2.1 | XL2 | XC2.2 | ||||||||
| Величина сопротивления (Ом) | |||||||||||||||
| R1 | XL1.1 | XC1 | XL1.2 | R2 | XC2.1 | XL2 | XC2.2 | ||||||||
| 58 | 0 | 10 | 0 | 20 | 0 | 0 | 20 | 10 | |||||||
| 59 | 10 | 0 | 40 | 0 | 20 | 30 | 20 | 0 | |||||||
| 60 | 10 | 0 | 40 | 20 | 20 | 30 | 0 | 10 | |||||||
| 61 | 10 | 10 | 0 | 0 | 20 | 30 | 0 | 0 | |||||||
| 62 | 10 | 10 | 0 | 20 | 20 | 0 | 20 | 10 | |||||||
| 63 | 10 | 10 | 40 | 0 | 20 | 0 | 20 | 0 | |||||||
| 64 | 0 | 0 | 40 | 20 | 0 | 30 | 20 | 0 | |||||||
| 65 | 0 | 10 | 40 | 0 | 0 | 0 | 20 | 10 | |||||||
| 66 | 10 | 0 | 40 | 20 | 20 | 30 | 20 | 0 | |||||||
| 67 | 10 | 10 | 0 | 0 | 20 | 30 | 0 | 10 | |||||||
| 68 | 10 | 10 | 0 | 20 | 20 | 30 | 0 | 0 | |||||||
| 69 | 10 | 10 | 40 | 0 | 20 | 0 | 20 | 10 | |||||||
| 70 | 0 | 0 | 40 | 20 | 0 | 30 | 20 | 10 | |||||||
| 71 | 0 | 10 | 0 | 20 | 0 | 30 | 0 | 10 | |||||||
| 72 | 0 | 10 | 40 | 0 | 20 | 0 | 20 | 0 | |||||||
|
| Поделиться: |

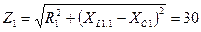 Ом.
Ом.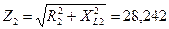 Ом.
Ом.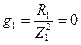 .
.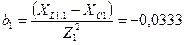 См.
См.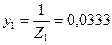 См.
См.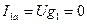 .
.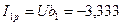 А.
А.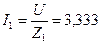 А.
А.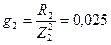 См.
См.
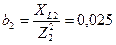 См.
См.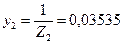 См.
См.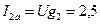 А.
А.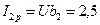 А.
А.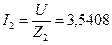 А.
А.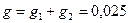 См.
См.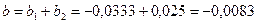 См.
См.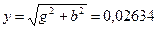 См.
См.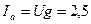 A.
A.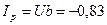 A.
A.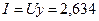 A.
A.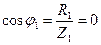 .
.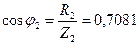 .
.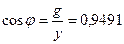 .
.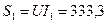 В.
В.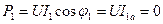 .
.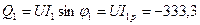 ВАр.
ВАр.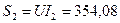 В.
В.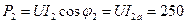 Вт.
Вт.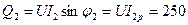 ВАр.
ВАр.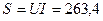 В.
В.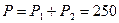 Вт.
Вт. ВАр.
ВАр.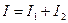 .
.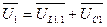 .
.
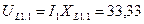 B.
B.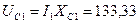 B.
B.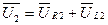 .
.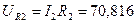 B.
B.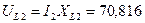 B.
B.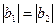 .
. необходимо в первую ветвь включить дополнительно емкость, величину сопротивления которого можно вычислить следующим образом:
необходимо в первую ветвь включить дополнительно емкость, величину сопротивления которого можно вычислить следующим образом: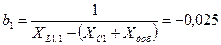 См,
См,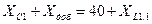 ,
,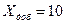 Ом.
Ом.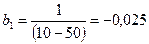 См,
См,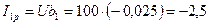 А,
А,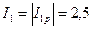 А,
А,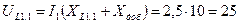 В,
В,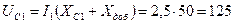 В.
В.