Режим изменения тока одной фазы
Рассмотрим режим работы трехфазной цепи, соединенной по схеме треугольник при изменении величины сопротивления одной фазы. Допустим, сопротивление фазы BC уменьшили, т.е.:
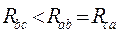 . .
Тогда согласно уравнению (4.3) точки  и и 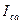 останутся неизменными, а ток фазы останутся неизменными, а ток фазы  увеличится: увеличится:
 . .
Для определения линейных токов 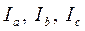 строим векторные диаграммы токов и напряжений аналогично симметричному режиму работы. Векторные диаграммы представлены на рис. 45. строим векторные диаграммы токов и напряжений аналогично симметричному режиму работы. Векторные диаграммы представлены на рис. 45.

Рисунок 45. Векторные диаграммы токов и напряжений
при изменении тока одной фазы для случая 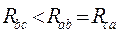
Сравнивая векторные диаграммы при симметричном режиме работы (рис. 44) и при изменении тока одной фазы (рис. 45) можно сделать следующие выводы:
1. При изменении тока в одной фазе токи в двух других фазах не изменяются (в нашем случае  и и 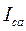 ). ).
2. При увеличении тока одной фазы, токи в линейных проводах, примыкающих к этой фазе, также увеличиваются (в нашем случае токи  и и 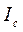 ). ).
3. Ток в третьем линейном проводе не изменяется (в нашем случае ток 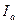 ). ).
Режим несимметричной нагрузки
Рассмотрим случай, когда нагрузка во всех фазах носит чисто активный характер, а между величинами сопротивлений фаз приемника справедливо следующее соотношение:
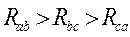 . .
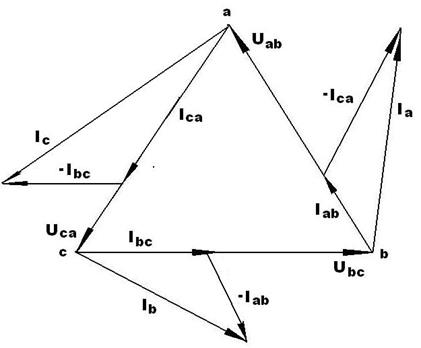
Рисунок 46. Векторные диаграммы токов и напряжений
при несимметричной нагрузке для случая 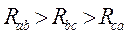
Тогда согласно системе уравнений (4.3) между величинами фазных токов будет справедливо следующее отношение:
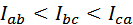
Для определения линейных токов  , , 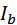 , ,  строим векторные диаграммы токов и напряжений. Векторные диаграммы строятся как при симметричной нагрузке. Векторная диаграмма представлена на рис. 46. строим векторные диаграммы токов и напряжений. Векторные диаграммы строятся как при симметричной нагрузке. Векторная диаграмма представлена на рис. 46.
Сравнивая векторные диаграммы при симметричной нагрузке (рис. 44) и несимметричной нагрузке (рис. 46), можно сделать следующий вывод: при несимметричной нагрузке фазные и линейные токи, соответственно, не равны по величине и режим работы отдельных фаз не зависит друг от друга.
Режим обрыва одной фазы
Рассмотрим, как измениться режим работы приёмников, соединённых по схеме треугольник, если произойдёт обрыв одной из фаз (допустим фазы ВС). Нагрузка до обрыва была симметричной. Данному случаю будет соответствовать следующее соотношение:
 , , 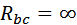 . .
Согласно системе уравнений (4.3) будем иметь:
 , , 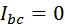 . .
Электрическая схема (рис. 42) при обрыве фазы 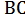 примет вид (рис. 47): примет вид (рис. 47):
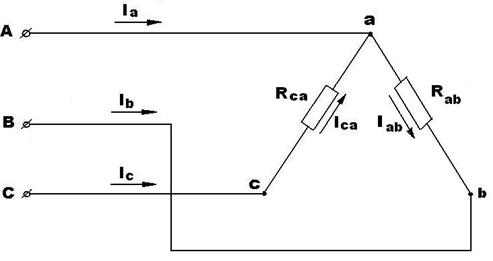
Рисунок 47. Электрическая схема при обрыве фазы BC
По электрической схеме, с учётом системы уравнений (4.5), по первому закону Кирхгофа можно составить следующую систему уравнений:
 (4.8) (4.8)
Для определения линейных токов  , , 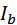 , ,  на рис. 48 изображена векторная диаграмма токов и напряжений, построенная согласно системе уравнений (4.8). на рис. 48 изображена векторная диаграмма токов и напряжений, построенная согласно системе уравнений (4.8).
Из анализа векторных диаграмм токов и напряжений при обрыве одной из фаз можно сделать следующие выводы:
1. Фазные напряжения  , , 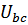 , , 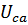 остаются неизменными. остаются неизменными.
2. Режим работы неповреждённых фаз не меняется.
3. Токи в линейных проводах, соединённых с оборванной фазой, становятся равными фазным токам.
4. Ток в третьем линейном проводе не меняется.
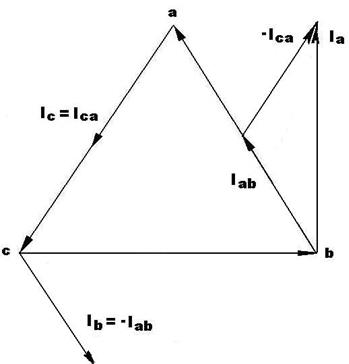
Рисунок 48. Векторная диаграмма токов и напряжений
при обрыве фазы BC
|