Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
XIII. Практическое занятие №5. Магнитные и нелинейные цепиСодержание книги
Похожие статьи вашей тематики
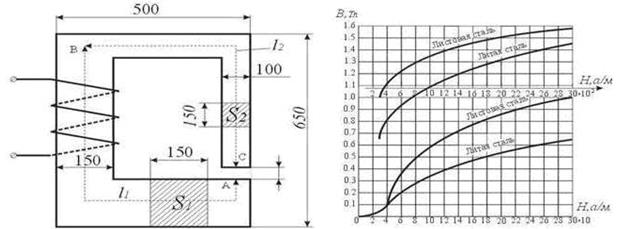
Поиск на нашем сайте 1. Вопросы для подготовки к занятиям Магнитные цепи с постоянным намагничивающим током: 1. Для чего сердечники электрических машин и аппаратов изготавливают из ферромагнитных материалов? 2. Дать понятие об однородной и неоднородной, разветвленной и неразветвленной магнитной цепи. 3. Закон полного тока для однородной и неоднородной магнитной цепи. 4. Алгоритм решения прямой и обратной задачи для однородной магнитной цепи. 5. Алгоритм решения прямой задачи для неоднородной магнитной цепи. 6. Алгоритм решения обратной задачи для неоднородной магнитной цепи 7. Как изменится индуктивность катушки при уменьшении длины воздушного зазора? 8. Как изменится ток в катушке при увеличении длины воздушного зазора? 9. Как изменится магнитный поток в сердечнике, если воздушный зазор заполнить прокладкой из ферромагнитного материала? 10. Как нужно изменить магнитодвижущую силу катушки, чтобы сохранить неизменным магнитный поток при увеличении длины воздушного зазора? 11. Как изменится индуктивность катушки, если в воздушный зазор положить ферромагнитную пластину? Магнитные цепи с переменным намагничивающим током 1. Какова форма тока в катушке и магнитного потока в сердечнике при синусоидальном приложенном напряжении? 2. Привести схему замещения и векторную диаграмму идеализированной катушки с сердечником (R =0, Xp =0). 3. Какие процессы в идеализированной катушке учитывают параметры ее схемы замещения? 4. Привести схему замещения и векторную диаграмму реальной катушки с сердечником. 5. Какие процессы в реальной катушке учитывают параметры ее схемы замещения? 6. Записать уравнение электрического равновесия для катушки с ферромагнитным сердечником и без него. 7. Зависит ли ток в катушке с ферромагнитным сердечником от материала сердечника и от наличия в нем воздушного зазора? 8. Как изменится амплитуда магнитного потока при увеличении длины воздушного зазора в сердечнике? 9. Как изменится ток в обмотке дросселя при увеличении длины воздушного зазора в сердечнике? 10. Как изменится индуктивность обмотки дросселя, если воздушный зазор в сердечнике заполнить ферромагнитной прокладкой? 11. Как изменится полное сопротивление обмотки дросселя, если увеличить длину воздушного зазора в сердечнике? 12. Зависит ли активная мощность, потребляемая из сети (активное сопротивление обмотки принять равным нулю) от величины приложенного напряжения? 13. Зависит ли потребляемая дросселем из сети активная мощность (при сопротивлении обмотки R =0) от частоты источника питания? 14. Зависит ли потребляемая дросселем из сети активная мощность (при сопротивлении обмотки R =0) от длины воздушного зазора в сердечнике? 15. Как изменится ток в обмотке дросселя при увеличении приложенного напряжения? 16. Как изменится индуктивность обмотки дросселя, если увеличить длину воздушного зазора в сердечнике? Примеры решения прямой и обратной задачи для магнитных цепей Задача 1. Рассмотрим магнитную цепь на рис. 114.
Необходимо создать магнитный поток Ф= 0,0165 Вб. Определить намагничивающая сила обмотки F. Задана кривая намагничивания стали (рис. 115) из которой выполнены ферромагнитные участки изображенного контура магнитной цепи (рис. 114). Решение. Используя рисунок определяем геометрические размеры участков: L 1=0,975 м, L 2=0,82 м, δ=0,002м, S 1=0,15×0,15=0,0225 м 2, S 2=0,1×0,15=0,015 м 2, S δ=0,1×0,15=0,015 м 2. Определим величину магнитной индукции на каждом участке: B 1 = Ф / S 1 = 0,0165 / 0,0225 = 0,735 Тл; B 2 = Ф / S 2 = 0,0165 / 0,015 = 1,1 Тл; B возд = Ф / S δ = 0,0165 / 0,015 = 1,1 Тл. Пользуясь кривой намагничивания для литой стали, определим напряжение магнитного поля в первом и во втором участках магнитной цепи: H1 = 350 А/м; H2 = 940 А/м. Напряженность в воздушном зазоре определяем из соотношения Hво зд = 8 × 105 × B возд = 8× 105 × 1,1 = 8,8× 105 А/м. Искомая намагничивающая сила обмотки: F = H1 L1 + H2 L2 + Hвозд δ = 350 × 0,975 + 940 × 0,82 + 8,8 × 105 × 0,002 = 2870 А. Обратим внимание на то, что 60% намагничивающей силы затрачивается на поддержание магнитного потока в воздушном зазоре, в то время как ширина зазора δ составляет <0,15% от общей длины магнитной цепи (b1+b2+δ). Этот факт является характерным для всех магнитных цепей и заставляет конструкторов электрических машин (во избежание чрезмерного увеличения намагничивающих сил обмоток) делать в магнитных цепях ширину воздушных зазоров возможно малой. Задача 2. Определить магнитный поток в воздушном зазоре магнитопровода (рис. 114), если намагничивающая сила обмотки F =2000 A B. Значения величины L 1, L 2, δ, S1, S 2, S δ взять из задачи 1. Решение. Для ориентировки предварительно определим магнитный поток Ф0 в цепи, учитывая только магнитное сопротивление воздушного зазора R возд =δ/(μ0Sδ) и пренебрегая сопротивлением ферромагнитных участков цепи:
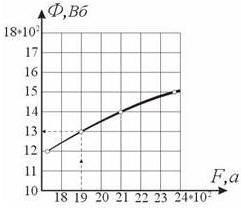
Поскольку магнитное сопротивление всей цепи несколько больше, чем сопротивление воздушного зазора, искомый магнитный поток меньше Ф0. Зададимся в предварительном расчете значением Ф ≈0,8 Ф0 =0,015 Вб и определим соответствующую этому потоку намагничивающую силу. Магнитная индукция на отдельных участках цепи: B 1 = Ф / S 1 = 0,015 / 0,0225 = 0,67 Тл; B 2 = Ф / S 2 = 0,015 / 0,015 = 1,0 Тл; B возд = Ф / S δ = 0,015 / 0,015 = 1,0 Тл. По кривой намагничивания для литой стали (рис. 115) находим: H 1 = 310 А/м, H2 = 700 А/м, Hвозд = 8× 105 А/м. Намагничивающая сила обмотки: F 1 = H1 L1 + H2 L 2 + H возд δ = 310 × 0,975 + 700 × 0,82 + 8 × 105 × 0,002 = 2470 А Далее зададимся еще значениями магнитного потока в 0,014 и 0,012 Вб и проведем аналогичные расчеты. Результаты всех расчетов сведены в табл. 13.1. По данным таблицы построен график Ф(F) (рис. 116). Из графика находим, что заданной намагничивающей силе F =2000 А соответствует магнитный поток Ф= 0,013 Вб. Таблица 13.1
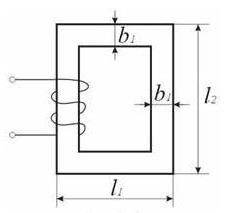
Рисунок 116 к задаче 2. График зависимости Ф(F) Задача 3. Определить число витков и ток в обмотке дросселя (рис. 117), сердечник которого изготовлен из листовой электротехнической стали Э41. Активным сопротивлением обмотки и потоком рассеяния пренебречь. Напряжение источника U =230 В, частота тока f =50 Гц, амплитуда магнитной индукции B m=1,4 Тл. Размеры сердечника: L 1=14 см; L 2=10 см; b 1=2 см; толщина сердечника b 2=3 см. Удельный вес стали γ=7,8 г/см3. Стальные листы разделены изоляцией, занимающей 10% всего объема. Определить ток в обмотке, если в сердечнике выпилить зазор толщиной δ =1 мм.
Рисунок 117 к задаче 3
Решение. Уравнение электрического равновесия для обмотки дросселя имеет вид:
где: R 1 – активное сопротивление обмотки; X 1 – индуктивное сопротивление обмотки, обусловленное потоком рассеяния; E =4,44 WФm – противо- ЭДС, наводимая в обмотке основным магнитным потоком; Фm – амплитуда основного магнитного потока. Согласно условию задачи R 1≈0, X 1≈0 из уравнения равновесия получаем: U = E = 4,44 W f Ф m, Ф m = B m S ст = 0,9 B m S, где: S ст – площадь поперечного сечения стали; S – площадь поперечного сечения магнитопровода, включая изоляцию между листами: S = b 1 b 2=2×10-2×3×10-2=6×10-4, м2. Число витков обмотки:
Рассмотрим ток в обмотке в виде двух составляющих: активной Ia, определяемой по мощности потерь в стали, и реактивной Ip (намагничивающий ток), зависящей от магнитный свойств цепи и определяемой по закону полного тока, тогда:
Активная составляющая тока: I а = P ст / U, P ст = p ст G, где: Рст – мощность потерь в стали; p ст – удельная мощность потерь в стали (таблица 13.2); G – вес стали. Найдем вес стальной части (без изоляции) магнитопровода: G = γ Sст Lст = 0,9 γ Sст. Длина средней силовой линии: L ст = 2 (L 1 - b 2) + 2 (L 2 - b 1) = 2 (12 + 8) = 40 см. Вес стали: G = 7,8 × 0,9 × 6 × 40 = 1,68 кг. Удельная мощность потерь в стали определяется соотношением: p ст = P B m2 / 50, в котором P /50=1,35 Вт (кг×Тл2) – удельная мощность потерь для данной марки стали (таблица 13.2) при индукции 1 Тл и частоте 50 Гц. Тогда: p ст=1,35×1,42=2,646 Вт/кг, а мощность потерь в стали: P ст=2,646×1,68=4,445 Вт. Активная составляющая тока: Ia = P ст / U = 4,445 / 230 = 0,019 A. Рассматриваемая магнитная цепь является однородной, поэтому на основании закона полного тока найдем амплитудное значение намагничивающего тока: Iрm = Hm L ст / W. Максимальное значение напряженности найдем по кривой намагничивания (таблица13.2) для стали Э41. При Вm =1,4 Тл, Нm =1300 А/м. Действующее значение намагничивающего тока:
Ток в обмотке:
Полученные результаты говорят о том, что в катушке с ферромагнитным сердечником активная составляющая тока невелика и можно принимать I ≈ Ip. Согласно уравнению электрического равновесия амплитуда магнитного потока Фm (или амплитуда магнитной индукции) пропорциональна приложенному напряжению U и не зависит от длины воздушного зазора. С появлением зазора будет изменяться только реактивная составляющая тока, которую найдем при помощи закона полного тока: I рm W = Hm Lст + H0m δ. Здесь H0mδ – составляющая МДС катушки, идущая на создание магнитного поля в воздушном зазоре: H0m = B m / μ0 = 1,4 / (4 π 10-7) = 11,146 × 105 А/м. I рm W = 1300 × 0,4 + 11,146 × 105 × 0,001 = 1634,6 А Таким образом, на создание магнитного поля в небольшом воздушном зазоре тратится большая част МДС. Действующее значение реактивной составляющей тока
Общий ток: I ≈ Ip = 0,846 А. Создание воздушного зазора длиной 1 мм привело к возрастанию тока в катушке в 3раза. 3. Самостоятельная работа студента Магнитные цепи с постоянными намагничивающими токами
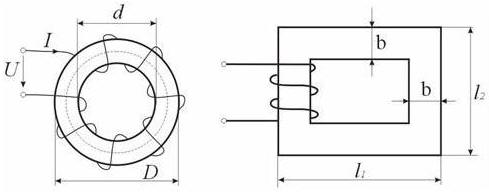
Задача 1. На тороидальный магнитопровод (рис.118) равномерно намотана обмотка с числом витков W =200, поперечное сечение кольца – прямоугольное, размеры кольца: D =16 см; d =10 см; толщина В =4 см. Определить ток в обмотке, при котором магнитный поток в сердечнике Ф= 12×10-4 Вб. Материал сердечника – электротехническая сталь Э42 (таблица 13.2). Ответ: 0,6 А. Таблица 13.2
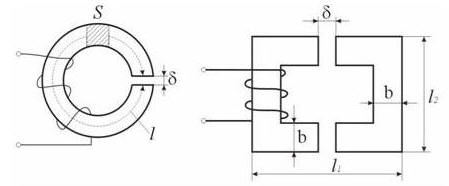
Задача 2. Найти индуктивность катушки, если ток в обмотке (рис. 119) I =20 А, число витков W =180, сердечник выполнен из стали Э42. Размеры сердечника: L 1=35 см; L 2=20 см; толщина сердечника b =6 см. Ответ: 49,5 мГн. Задача3. В сердечнике задачи №1 (рис. 118) пропилили зазор толщиной δ=0,1 см. Определить, как нужно изменить ток в катушке, чтобы магнитный поток в сердечнике не изменился. Ответ: 4,6 А. Задача 4. В сердечнике задачи №1 (рис. 118) сделан зазор толщиной δ =0,2 см. Ток в обмотке I =1,17 А. Определить величину магнитного потока, который будет создаваться в сердечнике при заданном токе. Задачу решить приближенно и с помощью построения магнитной характеристики. Сравнить полученные результаты. Ответ: 1,76 × 10-4 Вб; 1,7 × 10-4 Вб. Задача 5. Определить магнитодвижущую силу катушки (рис. 120) с сердечником из стали Э12, если Ф= 4×10-4 Вб, S =4 см 2, L =100 см, δ=0,02 см. Как изменится индуктивность катушки, если длину магнитного зазора увеличить? Ответ: 661 А, уменьшится. Задача 6. Определить магнитодвижущую силу катушки (рис. 121), размещенной на сердечнике из стали Э12, чтобы магнитная индукция в зазоре составляла B 0=0,852 Тл. Сердечник имеет одинаковую толщину. Размеры сердечника заданы: L 1=23 см, L 2=24 см, δ=0,01 см, b =4 см. Ответ: 393
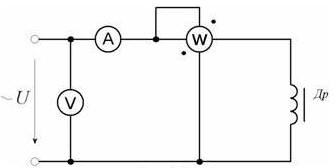
Магнитные цепи с переменными намагничивающими токами Задача 1. Даны показания приборов (рис. 122): Р=50 Вт, U =127 В, I =0,5 А. Активным сопротивлением обмотки и потоком рассеяния пренебречь. Построить векторную диаграмму. Определить параметры последовательной и параллельной схем замещения. Ответ: R 0 = 200 Ом, Х0 = 157 Ом, R 0 = 326 Ом, Х0 = 397 Ом.
Рисунок 122 к задачам для самостоятельной работы Задача 2. Показания приборов (рис. 122): Р =150 Вт, U =120 В, I =10 А. После удаления сердечника приборы показали: Р =72 Вт, U =120 В, I =12 А. Построить векторную диаграмму. Определить параметры последовательной схемы замещения. Потоком рассеяния пренебречь в катушке с сердечником. Ответ: R = 0,5 Ом, R 0 = 1 Ом, Х0 = 11,9 Ом. Задача 3. Ток в катушке со стальным сердечником I 1=2 А, мощность потерь Р1=20 Вт. Определить потери в меди и потери в стали, если при вынутом сердечнике ток и активная мощность имеют значения: I 2=8 А и Р 2=64 Вт. Ответ: РCu = 4 Вт, Р ст = 16 Вт. Задача 4. К сети переменного тока подключена катушка со стальным сердечником. Определить напряжение сети, активную и реактивную составляющие тока, если задано: Ф m=0,01 Вб, I =10 А, f =50 Гц, W =100, Р =400 Вт. Ответ: U = 222 В, Ia = 1,8 А, I р = 9,84 А. Задача 5. Сердечник из электротехнической стали вдвигаемой в катушку и служит для изменения индуктивности катушки. Напряжение сести U =220 В, частота сети f =50 Гц. Активное сопротивление катушки R =10 Ом, потерями в стали пренебречь. Построить векторную диаграмму и определить индуктивность катушки для трех случаев: а) при полностью вставленном сердечнике, если I 1=2 А; б) при частично вынутом сердечнике, если I 2=8 А; в) при полностью удаленном сердечнике, если I 3=15 А. Ответ: 350 мГн; 81,7 мГн; 34,2 мГн. Задача 6. Для катушки, приведенной в задаче 5, определить амплитуду магнитного потока, если число витков W =1000. Как изменится Фm, если частота уменьшится в 2 раза? Ответ: 99 × 10-5 Вб. Задача 7. Катушка имеет W =200витков и питается от сети переменного тока с частотой f =50 Гц, U =127 В. Ток в катушке I =6А, потребляемая из сети активная мощность Р =172 Вт. Сопротивление катушки, измеренное на постоянном токе, R =2 Ом. Построить векторную диаграмму. Определить индуктированную в катушке ЭДС Е, амплитуду магнитного потока Фm, cos φ, мощность потерь в меди Рм и в стали Рс т. Ответ: 123,7 В; 278,6 × 10-5 Вб; 0,226; 72 Вт; 100 Вт. Задача 8. Для определения амплитуды магнитной индукции Вm на сердечник катушки была намотана измерительная обмотка с числом витков W =60. Площадь сечения сердечника S ст=4 см2. При частоте f=50 Гц напряжение на измерительной обмотке U =7,5 В. Найти величину Вm. Ответ: 1,41 Тл.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 683; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

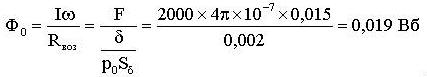 .
.
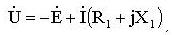
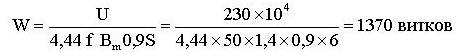 .
.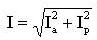 .
.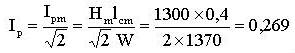 А.
А.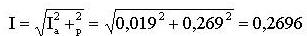 А.
А.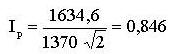 А.
А.