Общий случай разветвленной цепи
Для цепи, изображенной на рис. 133, на основании первого закона Кирхгофа для действующих значений токов можно записать
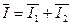 , ,

Рисунок 133. Общий случай разветвлённой цепи
где: 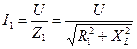 - ток первой ветви; - ток первой ветви;
 - ток второй ветви. - ток второй ветви.
На рис. 134 представлена векторная диаграмма для приведенной схемы.
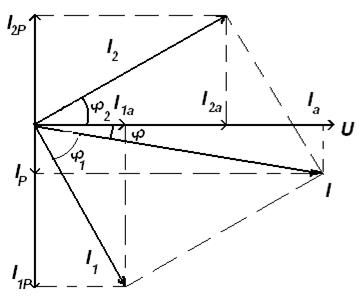
Рисунок 134. Векторная диаграмма токов и напряжений для общего случая разветвлённой цепи
Векторная диаграмма строилась в следующей последовательности:
1. за исходный вектор принимаем вектор напряжения на зажимах цепи, т.к. оно является общим для параллельных ветвей;
2. под углом φ1= arccos φ 1 по часовой стрелке относительно вектора U (т.к. ток в первой ветви носит активно-индуктивный характер и отстает по фазе от напряжения) строим вектор тока I 1;
3. под углом φ2= arccos φ 2 против часовой стрелки относительно вектора U (т.к. ток во второй ветви носит активно-емкостный характер и опережает по фазе напряжение) строим вектор тока I 2;
4. строим вектор тока в неразветвленной части цепи, как геометрическую сумму векторов токов I 1 и I 2 (диагональ параллелограмма, построенного на векторах I 1 и I 2).
Для аналитического сложения векторов необходимо их разложить на активные и реактивные составляющие. Анализируя векторную диаграмму после разложения векторов, легко заметить, что:
· активная составляющая тока в неразветвленной части цепи равна арифметической суммеактивных составляющих токов в параллельных ветвях
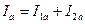 , (15.2) , (15.2)
· реактивная составляющая тока в неразветвленной части цепи равна алгебраической суммереактивных составляющих токов в параллельных ветвях
 , (15.3) , (15.3)
· полный ток в неразветвленной части цепи равен геометрической суммеполных токов в параллельных ветвях
 , (1.4) , (1.4)
Подставив в (15.2 – 15.3) значения активных и реактивных составляющих токов в параллельных ветвях получим:
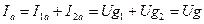 , ,
где: 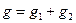 - эквивалентная активная проводимость всей цепи, равная арифметической суммеактивных проводимостей параллельных ветвей. - эквивалентная активная проводимость всей цепи, равная арифметической суммеактивных проводимостей параллельных ветвей.
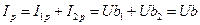 , ,
где: 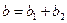 - эквивалентная реактивная проводимость всей цепи, равная алгебраической суммереактивных проводимостей параллельных ветвей. - эквивалентная реактивная проводимость всей цепи, равная алгебраической суммереактивных проводимостей параллельных ветвей.
Учитывая, что
I = U ∙ y,
и c учетом (15.4) получим:
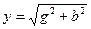 , ,
т.е. эквивалентная полная проводимость всей цепи равна геометрической суммеактивных и реактивных проводимостей всей цепи.
Коэффициент мощности всей цепи можно определить по формуле:
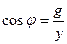 . .
Умножив вектора токов векторной диаграммы на U, получим:
· активная мощность всей цепи равна арифметической сумме активных мощностей параллельных ветвей:
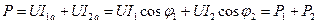 ; (15.5) ; (15.5)
· реактивная мощность всей цепи равна алгебраической сумме реактивных мощностей параллельных ветвей:
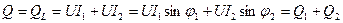 , (15.6) , (15.6)
Если Q >0, то вся цепь будет иметь активно-индуктивный характер, если Q <0 - активно-емкостный характер;
· полная (кажущаяся) мощность всей цепи равна геометрической сумме активной и реактивной мощностей всей цепи:
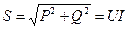 . .
Выражения (15.5) и (15.6) носят названия баланса активных и реактивных мощностей.
|