Параллельное соединение приёмников в цепях синусоидального тока
Основные положения и определения для электрических цепей переменного тока, а так же законы последовательного соединения активного сопротивления, катушки индуктивности и конденсатора были рассмотрены в пунктах 2.1-2.3 лабораторной работы №1. Рассмотрим другой случай включения в электрическую цепь различных элементов цепи.
На рис. 16 показана схема параллельного соединения приемников и соответствующая ей векторная диаграмма, на которой за исходный вектор принят вектор напряжения, так как он является общим для параллельных ветвей. Вектор тока Ie опережает по фазе вектор напряжения на угол 90°, а вектор тока I 1 отстает по фазе от вектора напряжения на угол φ1, т.к. характер нагрузки первой ветви активно-индуктивный.
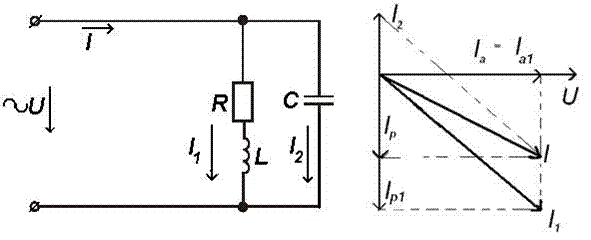
а) б)
Рисунок 16. Схема (а) и векторная диаграмма (б) цепи, состоящей из двух параллельных ветвей.
Согласно первому закону Кирхгофа, мгновенное значение тока в неразветвленной части цепи равно алгебраической сумме мгновенных значений токов в ветвях:
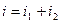 . .
Для действующих значений токов алгебраическая сумма заменяется геометрической, т.е. для рис. 16 б вектор общего тока равен геометрической сумме векторов тока 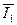 и и 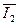 : :
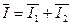 . .
Вектор общего тока можно выразить через активную и реактивную составляющие тока:
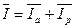 . .
Полученный треугольник ОАВ (рис. 17 а, б) называется треугольник ом токов. Очевидно, что:
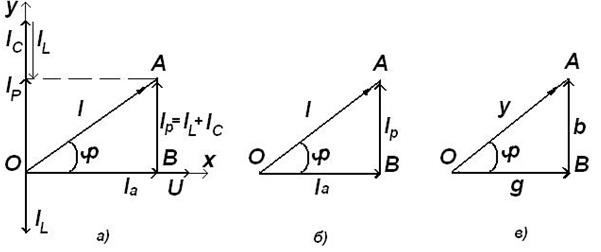
Рисунок 17. Векторная диаграмма для параллельной цепи (а), треугольник токов (б) и треугольник проводимостей (в)
Разделив модули векторов треугольника на приложенное напряжение, получим треугольники скалярных величин – полной (у), активной (g) и реактивной (в) проводимостей (рис. 17 в). Где:
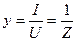 , ,
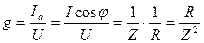 , ,
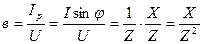 . .
Из треугольника проводимостей следует, что:
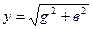 , , 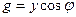 , , 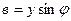 , ,
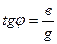 . .
Активная составляющая общего тока (см. рис. 16 б) равна арифметической сумме активных составляющих токов ветвей:
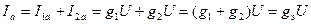 , ,
и реактивная составляющая равна алгебраической сумме реактивных составляющих этих токов:
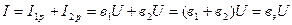 . .
Из вышеприведенных выражений следует, что эквивалентная активная проводимость цепи равна арифметической сумме активных проводимостей параллельно включенных ветвей:
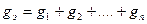 , ,
а эквивалентная реактивная проводимость – алгебраической сумме реактивных проводимостей параллельно включенных ветвей:
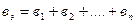 . .
При этом проводимости ветвей с емкостным характером нагрузки берут со знаком «минус», ветвей с индуктивным характером со знаком «плюс». На основании векторной диаграммы (рис. 16 б) можно написать аналитическое выражение мгновенных значений напряжения и токов цепи (рис. 16 а). если принять, что
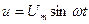 , ,
то: 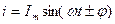 , ,
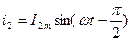 , ,
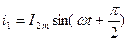 . .
|