Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрические цепи с активным сопротивлением, индуктивностью и ёмкостьюСодержание книги
Поиск на нашем сайте
В цепях с изменяющимися во времени токами, кроме процессов преобразования электроэнергии в другие виды энергии, наблюдаются процессы, обусловленные изменением энергии магнитных и электрических полей. Чтобы учесть эти процессы при построении электрических схем, используют три параметра: активное сопротивление R, индуктивность L, емкость С, характеризующие такие элементы цепи, как резисторы, катушки и конденсаторы. Сопротивление цепи переменного тока, в котором происходит необратимое преобразование электрической энергии в тепловую, называется активным сопротивлением R. В цепи с активным сопротивлением рис. 4, а ток совпадает по фазе с приложенным напряжением, т.е.
Рисунок 4. Схема (а), временная (б), и векторная диаграммы цепи с резисторным элементом
Действующие значения тока и напряжения связаны законом Ом а:
Индуктивным элемент омназывается идеализированный элемент электрической цепи (
При переменном токе сопровождающее его магнитное поле изменяется во времени. На основании закона электромагнитной индукции Фарадея-Максвелла появляется ЭДС самоиндукции
По закону Ленца, выражающему принцип электромагнитной инерции, эта ЭДС противодействует изменению потокосцепления, что и учитывается знаком минус. Если L не зависит от i, т.е. рассматриваемая цепь линейна, то
Величина:
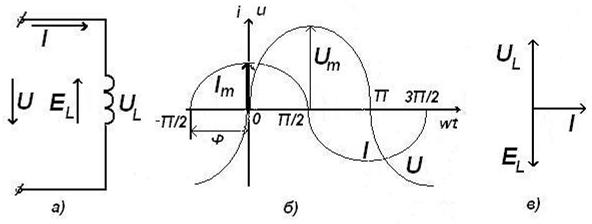
называется падением напряжения в индуктивности. Для цепи с индуктивностью (рис. 5, а), где
т. е. индуктивное падение напряжения опережает ток на 90° (рис. 5, б, в).
Рисунок 5. Схема (а), временная (б), и векторная диаграммы цепи с индуктивной катушкой
Действующее значение напряжения
Величину
При рассмотрении реальных катушек необходимо учитывать, что в отличие от идеальных, их активное сопротивление RL не равно 0. Емкость учитывает влияние изменяющегося электрического поля элементов цепи и может быть определена как отношение заряда к напряжению на емкостном элементе:
При включении емкости при напряжение
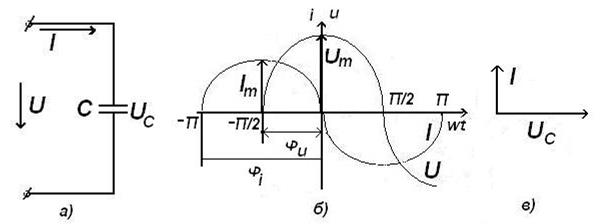
Следовательно, ток опережает напряжение на емкости на 90°(рис. 6, б, в)
Рисунок 6. Схема (а), временная (б), и векторная диаграммы цепи с идеальным конденсатором
Действующее значение тока:
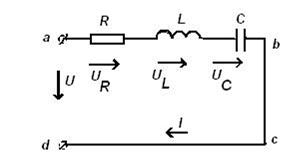
Величина 2.3. Последовательное соединение элементов с параметрами R, L, С Схема неразветвленной цепи синусоидального тока представлена на рис. 7. Энергетическое состояние цепи описывается для мгновенных значений уравнением:
Рисунок 7. Схема последовательного соединения элементов цепи Если
Это уравнение позволяет построить временную диаграмму, которая полностью отражает амплитудные и фазовые соотношения в последовательной цепи. Для практических расчетов применяют векторные диаграммы, которые делают расчет цепи более наглядным и простым. Под векторной диаграммой цепи понимают совокупность векторов ЭДС, напряжений и токов электрической цепи, построенных с соблюдением их взаимной ориентации по фазе. Так как чаще при анализе и расчете электрической цепи пользуются действующими значениями токов и напряжений, векторную диаграмму, как графическую интерпретацию расчета цепи, строят также для действующих значений напряжений и токов. При построении векторной диаграммы в качестве исходного вектора удобнее выбрать вектор величин, одинаковой для нескольких элементов цепи. В последовательной цепи (рис. 7) по всем участкам проходит один и тот же ток, поэтому за исходный вектор выбирается вектор тока и относительно его строятся под углом сдвига На топографической векторной диаграмме каждая точка соответствует определенной точке электрической цепи. Чтобы осуществить это соответствие точек диаграммы и цепи, построение векторов топографической диаграммы ведут в той же последовательности, в какой обходят электрическую цепь. На рис. 8 показана топографическая диаграмма для цепи рис. 7.
Обход цепи начат от точки «d». При переходе к точке «с» потенциал увеличивается на величину падения напряжения на емкости
Рисунок 8. Векторная диаграмма токов и напряжений при последовательном соединении элементов цепи
В зависимости от величин L и С возможны следующие варианты: XL>XC; XL<XC; XL=XC. Для варианта XL>XC , угол φ>0, UL>UC. Ток отстает от напряжения на угол φ. Цепь имеет активно-индуктивный характер. Векторная диаграмма напряжений имеет вид как на рис. 9.
Рисунок 9. Векторная диаграмма напряжений для варианта XL>XC , угол φ>0, U L> U C Для варианта XL<XC угол φ<0, UL<UC. Ток опережает напряжение на угол φ. Цепь имеет активно-емкостный характер. Векторная диаграмма напряжений имеет вид как на рис.10.
Рисунок 10. Векторная диаграмма напряжений для варианта XL<XC угол φ<0, U L< U C
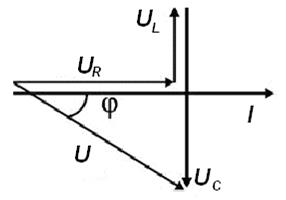
Для варианта XL=XC , угол φ=0, UL=UC. Ток совпадает с напряжением. Цепь имеет активный характер. Полное сопротивление Z =R наименьшее из всех возможных значений XL и XC. Векторная диаграмма напряжений имеет вид (рис.11).
Рисунок 11. Векторная диаграмма напряжений для варианта XL=XC , угол φ=0, UL=UC
Этот режим называется резонанс напряжений (UL=UC). Напряжения на элементах UL и UC могут значительно превышать входное напряжение. На векторной диаграмме рис. 9 или рис. 10 можно выделить треугольник, который принято называть треугольник ом напряжения. В этом треугольнике:
где
Очевидно:
Поделив модули вектора треугольника напряжений на ток, получим подобный ему треугольник сопротивлений рис. 12.,
Рисунок 12. Треугольник сопротивлений где:
От треугольника напряжений легко перейти также к треугольнику мощностей рис. 13.
Рисунок 13. Треугольник мощностей.
В этом треугольнике:
называется коэффициент ом мощности цепи. Используя векторную диаграмму (см. рис. 8) можно написать аналитические выражения для мгновенных значений тока и напряжений. Так для рис. 7, если:
то
Последовательная цепь может содержать большое число приемников с различными значениями R, L, С. При этом активные сопротивления, напряжения и мощности отдельных приемников складываются арифметически:
Реактивные сопротивления, напряжения и мощности отдельных приемников складываются алгебраически:
при этом величины, относящиеся к индуктивности, входит в сумму со знаком «плюс», а величины, относящиеся к емкости со знаком «минус». Полные сопротивления, напряжения и мощности отдельных приемников складываются геометрически.
ЛАБОРАТОРНАЯ УСТАНОВКА Лабораторная работа выполняется на универсальном стенде. Источником питания служит автотрансформатор, с помощью которого можно изменять напряжение от 0 до 250 В. Катушка индуктивности, батарея конденсаторов и электроизмерительные приборы установлены на стенде. В качестве вольтметра используется ампервольтметр АВО-63 или мультиметр ВР-11. Внимание: Измерения напряжения начинать на максимальном пределе измерения, если показания приборов будут малы, последовательно переходить на меньший предел измерения. ПРОГРАММА РАБОТЫ Экспериментальная часть 4.1.1. Ознакомиться с лабораторной установкой и измерительными приборами. Определить цены делений приборов. 4.1.2. Собрать электрическую цепь по схеме рис. 14. Включить осциллограф. Подготовить вольтметр к работе. 4.1.3. После проверки схемы преподавателем и получения вырианта задания (таблица 1.2) подать на стенд переменное напряжение и измерить ток, мощность и напряжение на участках цепи при 4.1.4. Повторить пункты 4.1.3 для другого значения Зарисовать кривые напряжений на участках цепи Примечание: при эксперименте коэффициент усиления не изменять.
Рисунок 14. Принципиальная схема лабораторной установки.
|
|||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.42.190 (0.012 с.) |

 =0 (рис. 4, б, в)
=0 (рис. 4, б, в)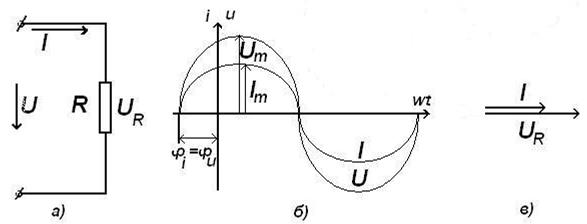
 .
.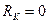 ), приближающийся по свойствам к индуктивной катушке, в которой накапливается энергия магнитного поля. При этом термин «индуктивность» характеризует свойство цепи накапливать энергию магнитного поля. Она является количественной оценкой отношения потокосцепления
), приближающийся по свойствам к индуктивной катушке, в которой накапливается энергия магнитного поля. При этом термин «индуктивность» характеризует свойство цепи накапливать энергию магнитного поля. Она является количественной оценкой отношения потокосцепления 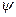 рассматриваемого контура к току, его создающему:
рассматриваемого контура к току, его создающему: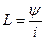 .
.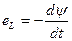 .
.
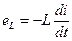 .
.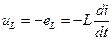
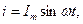
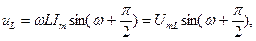
 .
.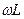 принято называть реактивным индуктивнымсопротивлени ем и обозначается через XL
принято называть реактивным индуктивнымсопротивлени ем и обозначается через XL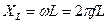 , [ Ом ].
, [ Ом ].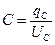 .
. (рис. 6, а) в цепи появляется ток:
(рис. 6, а) в цепи появляется ток: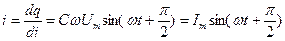
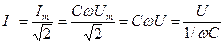 .
.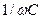 , имеющая размерность сопротивления (Ом), называется реактивным емкостным сопротивлением и обозначается XC:
, имеющая размерность сопротивления (Ом), называется реактивным емкостным сопротивлением и обозначается XC: 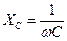 .
.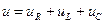 ,
, 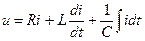 ,
,

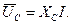 Вектор этого падения напряжения
Вектор этого падения напряжения 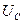 отстает от вектора тока I на угол 90°. Потенциал точки «в» выше потенциала точки «с» на величину падения напряжения на втором участке, вектор которого
отстает от вектора тока I на угол 90°. Потенциал точки «в» выше потенциала точки «с» на величину падения напряжения на втором участке, вектор которого 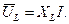 опережает по фазе вектор тока на угол 90°. Потенциал точки «а» выше потенциала точки «в» на величину падения напряжения
опережает по фазе вектор тока на угол 90°. Потенциал точки «а» выше потенциала точки «в» на величину падения напряжения  вектор, которого совпадает с вектором тока. Вектор результирующего напряжения расположен между точками «а» и «d».
вектор, которого совпадает с вектором тока. Вектор результирующего напряжения расположен между точками «а» и «d».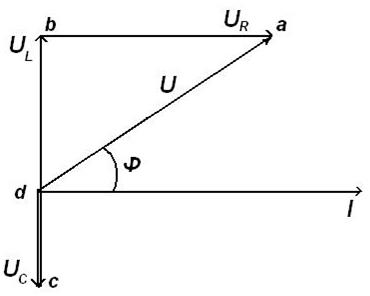

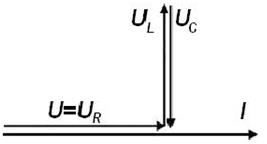

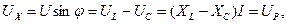
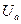 ‑ активная составляющая напряжения;
‑ активная составляющая напряжения; — реактивная составляющая напряжения.
— реактивная составляющая напряжения.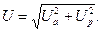
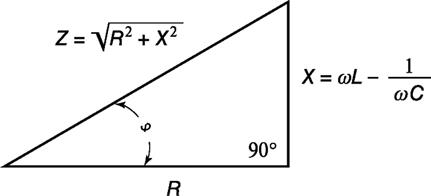
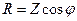 – активное сопротивление цепи;
– активное сопротивление цепи;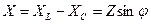 - реактивное сопротивление цепи;
- реактивное сопротивление цепи; - полное сопротивление цепи.
- полное сопротивление цепи.
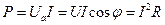 ‑ активная мощность цепи
‑ активная мощность цепи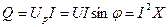 ‑ реактивная мощность цепи
‑ реактивная мощность цепи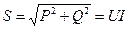 ‑ полная мощность цепи
‑ полная мощность цепи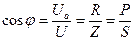
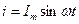
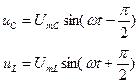 .
.
 .
.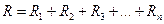
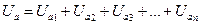


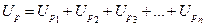
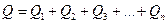
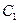 и трех различных сопротивлений
и трех различных сопротивлений 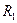 . Результаты измерений занести в таблицу.1.1.
. Результаты измерений занести в таблицу.1.1.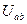 ,
, 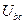 ,
, 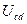 ,
,  (см. рис. 15), наблюдая их на экране осциллографа. Для этого провода от осциллографа поочередно подсоединить ко всем участкам цепи. Учитывая, что напряжения и ток на активном сопротивлении
(см. рис. 15), наблюдая их на экране осциллографа. Для этого провода от осциллографа поочередно подсоединить ко всем участкам цепи. Учитывая, что напряжения и ток на активном сопротивлении