
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретні передавальні функції і структурні схемиСодержание книги
Поиск на нашем сайте
де Пристрій, який формує послідовність імпульсів в залежності від вхідного сигналу, називається імпульсним елементом. Миттєвий імпульс представляють дельта-функцією:
зображення якої
Зображення його вихідного сигналу
За умови
Зображенням (16.15) є функція
оскільки зображенням за Лапласом одиничної функції За вхідного сигналу
Екстраполятор разом з неперервною ланкою називають приведе - ною ланкою, передавальна функція якої
де Остання ланка на рис. 16.4 здійснює перетворення вихідного сиг-налу
Рис. 16.4. Структурна схема імпульсного елемента і неперервної ланки
Застосувавши
Оскільки
де
На підставі структурної схеми на рис. 16.4 складають структурну схему замкненого контуру цифрової системи керування електро-приводом (рис. 16.5). Неперервною ланкою у цій схемі є об’єкт ке-рування з передавальною функцією
Рис. 16.5. Структурна схема цифрового контуру регулювання
Для даної структурної схеми дискретна передавальна функція приведеної ланки
Дискретна передавальна функція розімкненого контуру
де Щоби визначити динамічні показники наведеної системи регу-лювання, необхідно розрахувати перехідну функцію замкненого контуру
використавши формули розкладання функції
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.116.234 (0.006 с.) |

 Математичною основою опису динаміки електропривода з ЦСК без врахування квантування за рівнем є теорія імпульсних систем, оскільки неперервний сигнал
Математичною основою опису динаміки електропривода з ЦСК без врахування квантування за рівнем є теорія імпульсних систем, оскільки неперервний сигнал  перетворюється у квантований за часом імпульсний сигнал
перетворюється у квантований за часом імпульсний сигнал  з амплітудно-імпульсною модуляцією з
з амплітудно-імпульсною модуляцією з 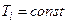 . При цьому амплітуда імпульсу дорівнює миттєвому значенню
. При цьому амплітуда імпульсу дорівнює миттєвому значенню  на початку періоду дискретності
на початку періоду дискретності  (рис. 16.3).
(рис. 16.3). За
За  послідовність імпульсних сигналів перетво-рюється у так звану решітчас-ту функцію
послідовність імпульсних сигналів перетво-рюється у так звану решітчас-ту функцію 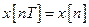 , цілечисельний аргумент якої визначається номером такта
, цілечисельний аргумент якої визначається номером такта  часової дискретності. Розрахун-ки імпульсних систем, як і систем аналогових, проводять з ви-користанням перетворення Лапласа, але у формі дискретного
часової дискретності. Розрахун-ки імпульсних систем, як і систем аналогових, проводять з ви-користанням перетворення Лапласа, але у формі дискретного  - пе-ретворення:
- пе-ретворення: , (16.11)
, (16.11) – решітчаста функція – оригінал;
– решітчаста функція – оригінал;  – зображення ре-шітчастої функції;
– зображення ре-шітчастої функції;  .
. при
при  ;
; при
при 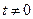 , (16.12)
, (16.12) . Згідно (16.12) імпульсний елемент опи-сується рівняннями
. Згідно (16.12) імпульсний елемент опи-сується рівняннями при
при  ;
; при
при  . (16.13)
. (16.13) . (16.14)
. (16.14) імпульсний елемент представляють ланкою перетворення неперервного сигналу
імпульсний елемент представляють ланкою перетворення неперервного сигналу  і екстраполятора (рис.16.4), вихідна величина якого
і екстраполятора (рис.16.4), вихідна величина якого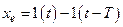 . (16.15)
. (16.15) ,
, є
є  .
. . (16.16)
. (16.16) , (16.17)
, (16.17) – передавальна функція неперервної ланки.
– передавальна функція неперервної ланки.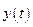 неперервної ланки у решітчасту функцію
неперервної ланки у решітчасту функцію  .
.
 -перетворення до (16.17), отримаємо дискретну передавальну функцію приведеної ланки:
-перетворення до (16.17), отримаємо дискретну передавальну функцію приведеної ланки: . (16.18)
. (16.18) є зображення функції
є зображення функції  є зображе-нням перехідної функції
є зображе-нням перехідної функції  неперервної ланки, тобто це реакція неперервної ланки на одиничний імпульс. Отже, можна записати, що
неперервної ланки, тобто це реакція неперервної ланки на одиничний імпульс. Отже, можна записати, що  і дискретна передавальна функція
і дискретна передавальна функція , (16.19)
, (16.19) – перехідна решітчаста функція неперервної ланки.
– перехідна решітчаста функція неперервної ланки. , вихідною змінною якою може бути струм, момент, кутова швидкість чи переміщення.
, вихідною змінною якою може бути струм, момент, кутова швидкість чи переміщення.
 . (16.20)
. (16.20) , (16.21)
, (16.21) – дискретна передавальна функція цифрового регулято-ра.
– дискретна передавальна функція цифрового регулято-ра. для вхідного сигналу
для вхідного сигналу  , за якою визначають перерегулювання і час регулювання. Дійсний перехідний процес
, за якою визначають перерегулювання і час регулювання. Дійсний перехідний процес 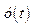 розраховують за передавальною функцією замкненої системи
розраховують за передавальною функцією замкненої системи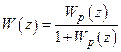 , (16.22)
, (16.22) , або методом різницевих рівнянь.
, або методом різницевих рівнянь.


