
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Часові характеристики двигунів постійного струму незалежного збудження
Двигуни постійного струму незалежного збудження використо-вуються, в основному, в замкнених системах керування. Для розра-хунку параметрів таких систем необхідно знати часові та частотні характеристик двигуна як об’єкта керування. Тому треба знати як протікають перехідні процеси в часі і як їх можна представити на комплексній площині. Перехідні процеси виникають при переході електропривода з одного усталеного режиму до другого. Знання цих процесів дозво-ляє правильно вибрати потужність двигуна, розрахувати систему керування і оцінити вплив електропривода на продуктивність і якість роботи виробничих механізмів. В перехідному процесі одночасно і взаємозв’язано протікають перехідні механічний, електромагнітний і тепловий процеси. Час перехідних процесів незначний і вони суттєво не впливають на зміну теплового стану електропривода і ним нехтують. Тому у подальшому будуть аналізуватись лише механічний і електромагнітний перехідні процеси, які називають електромеханічним перехідним процесом. Він зумовлений електромагнітною інерцією обмоток двигуна і механічною інерцією рухомих частин електропривода. При сталому магнітному потоці обмотки збудження
З врахуванням, що
де Диференціальному рівнянню (3.22) відповідає характеристичне рівняння
З (3.23) слідує, що за умов: Ø Ø Ø Якщо
де Рівняння струму якоря у перехідному процесі
За умови
де Криві швидкості і струму (рис.3.15,а), побудовані згідно рівнянь (3.26), показують, що кутова швидкість асимптотично наближається до
асимптотично наближається до нуля, бо
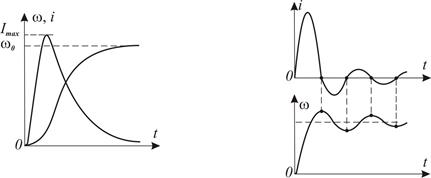
Рис.3.15. Графіки зміни швидкості і струму у перехідному процесі у випадках від’ємних (а) і комплексних (б) коренів характеристичного рівняння при стрибку напруги
У випадку Комплексним кореням за умови
де З (3.27) і (3.28) випливає, що зміна кутової швидкості і струму мають вид затухаючих коливань (рис.3.15,б). Перехідні процеси, зумовлені миттєвим збільшенням моменту сил опору від нуля до
У випадку зміни магнітного потоку, зумовленого зміною напруги збудження з
В результаті отримаємо нелінійне диференціальне рівняння ІІІ-го по-рядку, яким буде описуватись пере-хідний процес при змінні напруги збудження.
Частотні характеристики
Їх утримують підстановкою
Передавальна функція за збуренням
Передавальній функції (3.29) відповідає амплітудно-фазова частотна характеристика
З (3.31) знаходять амплітудночастотну
(3.32) і фазочастотну
характеристики.
Залежність (3.33) показує, що при
Контрольні запитання і задачі
1. Чому механічні характеристики двигуна постійного струму незалежного збудження при зміні напруги живлення будуть парале-льними?
2. За якою формулою визначають коефіцієнт передачі двигуна постійного струму незалежного збудження? 3. Визначити коефіцієнт передачі двигуна постійного струму незалежного збудження, якщо 4. Яким способом треба регулювати кутову швидкість двигуна постійного струму незалежного збудження, щоби його потуж-ність не змінювалась? 5. Які характеристики використовують для побудови натураль-ної механічної характеристики двигуна постійного струму послідов-ного збудження? 6. Як здійснюють динамічне гальмування двигуна постійного струму послідовного збудження? 7. Що відбудеться з двигуном постійного струму послідовного збудження, якщо змінити полярність напруги живлення? 8. Від чого залежить вид перехідного процесу у двигуні постій-ного струму незалежного збудження? 9. За якої умови в двигуні постійного струму незалежного збудження виникає згасаючий коливальний перехідний процес? 10. Від яких параметрів залежить частота власних коливань двигуна постійного струму незалежного збудження? Розділ 4
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 361; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.131.168 (0.017 с.) |

 електромеханічний перехідний процес описується рівнян-нями електричної і механічної рівноваги:
електромеханічний перехідний процес описується рівнян-нями електричної і механічної рівноваги: ;
; ; (3.21)
; (3.21) .
. і
і 
 , розв’язком системи рівнянь (3.21) відносно
, розв’язком системи рівнянь (3.21) відносно 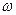 буде.
буде. , (3.22)
, (3.22) – електромеханічна стала часу;
– електромеханічна стала часу;  – електро-магнітна стала часу;
– електро-магнітна стала часу;  – індуктивність кола якоря.
– індуктивність кола якоря. , корені якого
, корені якого . (3.23)
. (3.23) корені будуть дійсними від’ємними числами;
корені будуть дійсними від’ємними числами;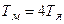 корені будуть рівними
корені будуть рівними  ;
; корені будуть комплексними числами.
корені будуть комплексними числами.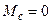 , то розв’язок (3.22) матиме вид:
, то розв’язок (3.22) матиме вид: , (3.24)
, (3.24)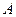 ,
, 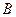 – сталі інтегрування, які визначають із початкових умов,
– сталі інтегрування, які визначають із початкових умов,  і
і  ;
;  – швидкість ідеального холос-того ходу.
– швидкість ідеального холос-того ходу. . (3.25)
. (3.25)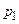 і
і  будуть від’єм-ними числами і залежності для швидкості і струму матимуть такий вид:
будуть від’єм-ними числами і залежності для швидкості і струму матимуть такий вид: ;
; , (3.26)
, (3.26) .
.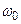 , а струм, досягнувши максимального значення
, а струм, досягнувши максимального значення ,
, , де
, де  і
і  .
. ; (3.27)
; (3.27) , (3.28)
, (3.28)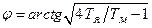 .
. , описуються також рівнянням (3.22), криві розв’язку якого наведено на рис.3.16 для випадку комплексних коренів. На рис.3.16
, описуються також рівнянням (3.22), криві розв’язку якого наведено на рис.3.16 для випадку комплексних коренів. На рис.3.16  .
. У випадку кратних від’ємних коренів перехідний процес
У випадку кратних від’ємних коренів перехідний процес  буде граничним між аперіодичним і коливально-затухаючим процесами.
буде граничним між аперіодичним і коливально-затухаючим процесами. до
до  і сталій напрузі живлення якорного кола, систему рівнянь (3.21) потрібно доповнити рівняннями
і сталій напрузі живлення якорного кола, систему рівнянь (3.21) потрібно доповнити рівняннями
 ;
;  і
і  .
. у вирази передавальних функцій. Передавальна функція двигуна за керуючим впливом згідно (3.22)
у вирази передавальних функцій. Передавальна функція двигуна за керуючим впливом згідно (3.22) . (3.29)
. (3.29) . (3.30)
. (3.30) .(3.31)
.(3.31)

 (3.33)
(3.33) З (3.32) слідує, що за
З (3.32) слідує, що за 
 . При
. При 
 характеристика
характеристика 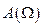 досягає максимального значення у випадку згасаючого перехідного процесу (крива 1 на рис.3.17). Для аперіодичного процесу амплітуда коливань зі зростанням частоти зменшується (крива 2 на рис.3.17).
досягає максимального значення у випадку згасаючого перехідного процесу (крива 1 на рис.3.17). Для аперіодичного процесу амплітуда коливань зі зростанням частоти зменшується (крива 2 на рис.3.17). , а при
, а при 
 . При цьому через точку
. При цьому через точку 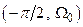 проходять фазо-частотні характеристики для різних видів коренів характеристичного рівняння.
проходять фазо-частотні характеристики для різних видів коренів характеристичного рівняння. ,
,  ,
, 
 і
і  .
.


