
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамічні показники слідкуючого електроприводаСодержание книги
Поиск на нашем сайте
Динамічні показники систем керування, зазвичай, визначають на підставі передавальних функцій. Для цього необхідно скласти рів-няння руху системи за рівняннями її елементів. Для слідкуючого електропривода, принципова схема якого зоб-ражена на рис. 15.2, запишемо рівняння елементів, вважаючи, що їх статичні характеристики лінійні. Рівняння сельсинів: рівняння розузгодження сельсинів давача і приймача
рівняння сельсина-приймача
де Рівняння фазочутливого підсилювача
де Рівняння двофазного асинхронного двигуна
де
Рівняння редуктора
На підставі рівнянь (15.6) – (15.10) складають структурну схему слідкуючого електропривода (рис.15.4).
Рис. 15.4. Структурна схема слідкуючого електропривода
На структурній схемі додатково показані диференціальна ланка з передавальною функцією Розв’язавши систему з рівнянь (15.6) – (15.10), отримаємо рівняння розімкненої системи
де Рівнянню (15.11) відповідає передавальна функція розімкненої системи
Якщо ротор С-Д обертати зі сталою швидкістю
Величина Перехідний процес в замкненій системі описує рівняння замкне-ної системи, яке отримаємо, підставивши в (15.11)
Рівняння (15.14) дозволяє визначити, за якого співвідношення
З (15.15) отримаємо умову стійкості:
з якої слідує, що добротність повинна бути меншою за критичну При проектуванні слідкуючого електропривода за вимогами тех-нологічного процесу визначають допустиму усталену похибку
Розглянемо такий приклад. Нехай Усталена похибка при Розглянемо, як впливає на добротність від’ємний зворотний зв'я-зок за швидкістю двигуна з коефіцієнтом
З врахуванням (15.18) рівняння руху розімкненої системи буде таким:
де Підставивши в (15.19)
Добротність системи зі зворотним зв’язком за швидкістю
З (15.21) випливає, що від’ємний зворотний зв'язок за швидкістю вихідного вала зменшує добротність системи у порівнянні з систе-мою без зворотного зв’язку, для якої вона дорівнює Для визначення впливу зворотного зв’язку на стійкість знайдемо рівняння рух замкненої системи, підставивши в (15.19)
характеристичне рівняння якого
Оскільки в (15.23) всі коефіцієнти додатні, то умова стійкості за критерієм Рауса матиме вид:
або
Нерівність (15.24) показує, що введення в систему додатково зво-ротного зв’язку за швидкістю двигуна покращує стійкість, оскільки
Окрім від’ємних зворотних зв’язків в слідкуючому електропри-воді використовують і додатні зв’язки, зокрема за похідною від по-хибки. За такого додаткового зв’язку з коефіцієнтом пропорційнос-ті
З врахуванням (15.25) рівняння руху розімкненої системи матиме вид:
де В усталеному режимі з
і добротність системи Підставивши в (15.26)
Рівнянню (15.28) відповідає характеристичне рівняння
і згідно критерію Рауса умова стійкості матиме вид:
або
оскільки всі коефіцієнти в (15.29) додатні. З (15.30) слідує, що введення зв’язку за похідною від похибки покращує стійкість системи і не змінює усталеної похибки у порівнянні з системою без такого зв’язку. Відомо, що для підвищення швидкодії використовують комбіно-вані системи керування – системи керування за відхиленням і за збуренням. Основним збуренням в слідкуючому електроприводі є задаючий сигнал. Тому розглянемо систему керування за відхилен-ням і похідною за задаючим сигналом (рис.15.4). Для такої системи напруга керування
де Розв’язавши систему рівнянь (15.6) – (15.11) з заміною (15.8) на (15.31), отримаємо рівняння замкненої комбінованої системи:
де Для визначення усталеної похибки необхідно знати передавальну функцію системи за похибкою Передавальна функція замкненої системи згідно (15.32)
Звідси
Передавальній функції Щоби визначити цей вплив, необхідно передавальну функцію
де
Застосувавши до ряду (15.35) обернене перетворення Лапласа, одержимо новий ряд у виді:
Кількість членів ряду (15.37), які використовують при розрахун-ках, залежить від виду задаючого сигналу. Так, для Згідно (15.36) коефіцієнти похибок
Отже, якщо
З (15.39) слідує, що похідна за задаючим сигналом зменшує уста-лену похибку на Якщо
Рівняння (15.40) показує, що при рівноприскореному русі задаю-чого валу усталена похибка буде наростати з часом і тільки за умови Отже, додаткові впливи від зворотного зв’язку за швидкістю, за похідною від похибки, чи задаючого сигналу дозволяють змінювати величину усталеної похибки. Одночасно змінюється передавальна функція замкненої системи і, як наслідок, – якісні показники пере-хідного процесу. Зміну останніх можна дослідити або за амплітуд-но-фазовими частотними характеристиками, визначаючи запас стій-кості за амплітудою і фазою, або за розв’язком рівняння руху замк-неної системи для різних законів зміни
а б в Рис. 15.5. Графіки
В режимі відпрацювання стрибка задаючого сигналу (позиційне керування) похибка змінюється від максимального значення до нуля і може мати коливально-затихаючий чи монотонний характер у за-лежності від виду коренів характеристичного рівняння системи (рис.15.5,а). Коли задаючий сигнал
Контрольні запитання і задачі
1. Що є структурною ознакою слідкуючого електропривода? 2. Що є характерним для дискретного слідкуючого електропри-вода? 3. Яке магнітне поле створює обмотка збудження сельсина-дава-ча? 4. Від чого залежить величина ЕРС, що наводиться в однофазній обмотці сельсина-приймача? 5. Якою буде усталена похибка в системі керування за похибкою, якщо добротність 6. Як впливає від’ємний зворотний зв'язок за швидкістю двигуна на добротність слідкуючого електропривода? 7. Якою повинна бути добротність системи керування за похиб-кою і її похідною, якщо усталена похибка 8. Як впливає додатковий вплив за похідною від похибки на стій-кість роботи слідкуючого електропривода? 9. В якій системі керування усталена похибка 10. У чому відмінність слідкуючого електропривода від позицій-ного електропривода? Розділ 16
Цифрові системи керування Електроприводами
|
|||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.95.167 (0.012 с.) |

 ; (15.6)
; (15.6) , (15.7)
, (15.7)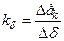 – крутизна характеристики
– крутизна характеристики  при
при 
 .
. , (15.8)
, (15.8) – коефіцієнт підсилення підсилювача.
– коефіцієнт підсилення підсилювача.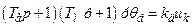 , (15.9)
, (15.9) – еквівалентна електромагнітна стала часу кіл статора і рото-ра, яку можна наближено визначити за формулою
– еквівалентна електромагнітна стала часу кіл статора і рото-ра, яку можна наближено визначити за формулою  ;
; – електромеханічна стала часу;
– електромеханічна стала часу;  – коефіцієнт жорсткості лінеарезованої частини механічної характеристики;
– коефіцієнт жорсткості лінеарезованої частини механічної характеристики;  – коефіцієнт передачі двигуна.
– коефіцієнт передачі двигуна. . (15.10)
. (15.10)
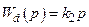 , зворотний зв’язок за швид-кістю з коефіцієнтом зворотного зв’язку
, зворотний зв’язок за швид-кістю з коефіцієнтом зворотного зв’язку 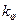 і момент статичного опору
і момент статичного опору  .
.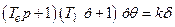 , (15.11)
, (15.11) ,
, 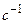 – коефіцієнт підсилення розімкненої системи.
– коефіцієнт підсилення розімкненої системи. . (15.12)
. (15.12)
 , то і ротор С-П буде обертатись з такою же швидкістю. Підставивши в (15.11)
, то і ротор С-П буде обертатись з такою же швидкістю. Підставивши в (15.11)  , що відповідає
, що відповідає  , і
, і  , одержимо рівняння руху слідкуючого електропривода в усталеному режимі:
, одержимо рівняння руху слідкуючого електропривода в усталеному режимі: . (15.13)
. (15.13)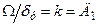 називається добротністю. Вона дозво-ляє визначити усталену похибку
називається добротністю. Вона дозво-ляє визначити усталену похибку  в режимі усталеного руху з
в режимі усталеного руху з  усталена похибка буде тим більша, чим менша добротність.
усталена похибка буде тим більша, чим менша добротність. :
: . (15.14)
. (15.14) і
і  система буде стійкою. За критерієм Рауса система буде стійкою, якщо коефіцієнти характеристичного рівняння
система буде стійкою. За критерієм Рауса система буде стійкою, якщо коефіцієнти характеристичного рівняння 
 будуть додатними числами і
будуть додатними числами і . (15.15)
. (15.15) , (15.16)
, (15.16) , за якої система знаходиться на межі стійкості. Зазвичай, величина добротності повинна бути меншою за критич-ну, щоби забезпечити запаси стійкості за амплітудою 3-4 і за фазою
, за якої система знаходиться на межі стійкості. Зазвичай, величина добротності повинна бути меншою за критич-ну, щоби забезпечити запаси стійкості за амплітудою 3-4 і за фазою  .
. при
при  . Тоді розрахункова добротність
. Тоді розрахункова добротність . (15.17)
. (15.17) ,
,  . Тоді
. Тоді  . Приймемо
. Приймемо  .
.

 . Якщо отримана похибка
. Якщо отримана похибка  більша
більша  , то необхідно збільшити добротність за рахунок або збільшення коефіцієнта підсилення підсилювача, або передбачити додаткові впливи від елементів, показаних на рис.15.4 пунктирними лініями.
, то необхідно збільшити добротність за рахунок або збільшення коефіцієнта підсилення підсилювача, або передбачити додаткові впливи від елементів, показаних на рис.15.4 пунктирними лініями. . (15.18)
. (15.18) , (15.19)
, (15.19) – інтенсивність керування за швидкості двигуна.
– інтенсивність керування за швидкості двигуна. і
і  , отримаємо рівняння руху в усталеному режимі
, отримаємо рівняння руху в усталеному режимі . (15. 20)
. (15. 20) . (15.21)
. (15.21) , (15.22)
, (15.22) . (15.23)
. (15.23)
 . (15.24)
. (15.24)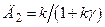 менше добротності
менше добротності  . Величину коефіцієнта
. Величину коефіцієнта 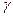 вибирають з умови запасу стійкості за фазою
вибирають з умови запасу стійкості за фазою 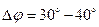 і за амплітудою, рівною 3-4. Крім того, цей зв'язок зменшує вплив мож-ливих змін сталих часу
і за амплітудою, рівною 3-4. Крім того, цей зв'язок зменшує вплив мож-ливих змін сталих часу  .
. напруга на виході підсилювача.
напруга на виході підсилювача. . (15.25)
. (15.25) , (15.26)
, (15.26) – інтенсивність керування за похідною похибки.
– інтенсивність керування за похідною похибки. рівняння (15.26) матиме вид
рівняння (15.26) матиме вид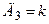 , тобто буде рівною добротності сис-теми без додаткових зв’язків
, тобто буде рівною добротності сис-теми без додаткових зв’язків  .
.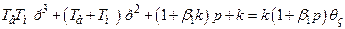 . (15.28)
. (15.28) (15.29)
(15.29)
 , (15.30)
, (15.30) , (15.31)
, (15.31) – коефіцієнт пропорційності.
– коефіцієнт пропорційності. , (15.32)
, (15.32) – інтенсивність керування за похідною від задаючо-го сигналу.
– інтенсивність керування за похідною від задаючо-го сигналу. , де
, де 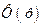 пере-давальна функція замкненої системи.
пере-давальна функція замкненої системи. . (15.33)
. (15.33)
 . (15.34)
. (15.34)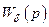 відповідає характеристичне рів-няння
відповідає характеристичне рів-няння  , яке не відрізняється від характеристичного рівняння системи з керуванням за відхиленням (похибкою). Отже, введення додаткового сигналу за похідною кута повороту вхідного вала не змінює стійкість комбінованої системи у порівнянні з системою керування тільки за похибкою, але вона впливає на величину усталеної похибки.
, яке не відрізняється від характеристичного рівняння системи з керуванням за відхиленням (похибкою). Отже, введення додаткового сигналу за похідною кута повороту вхідного вала не змінює стійкість комбінованої системи у порівнянні з системою керування тільки за похибкою, але вона впливає на величину усталеної похибки. , (15.35)
, (15.35) ,
,  ,
,  ,…,
,…,  – коефіцієнти похибок, які обчислюють за формулою
– коефіцієнти похибок, які обчислюють за формулою . (15.36)
. (15.36)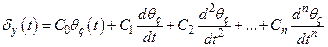 . (15.37)
. (15.37) , досить визначити за формулою (15.36) коефіцієнти
, досить визначити за формулою (15.36) коефіцієнти  – коефіцієнти
– коефіцієнти  , бо старші похідні будуть дорівнювати нулю.
, бо старші похідні будуть дорівнювати нулю. ;
; ;
; . (15.38)
. (15.38) . (15.39)
. (15.39) у порівнянні з системою керування за похиб-кою. За умови
у порівнянні з системою керування за похиб-кою. За умови  усталена похибка
усталена похибка  і система стає інваріантною по відношенню до зміни задаючого сигналу.
і система стає інваріантною по відношенню до зміни задаючого сигналу. – прискорення, то
– прискорення, то  ,
,  і усталена похибка
і усталена похибка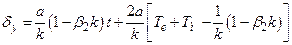 . (15.40)
. (15.40) .
.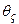 . Найбільш просто дослі-дити впливи додаткових зв’язків шляхом комп’ютерного моделюва-ння.
. Найбільш просто дослі-дити впливи додаткових зв’язків шляхом комп’ютерного моделюва-ння.
 і
і  у випадках
у випадках 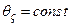 (а) і
(а) і  , а потім наближається до усталеного значення
, а потім наближається до усталеного значення  (рис.15.5,б) і тільки в системі з комбінованим керуванням усталена похибка з часом стає рівною нулю (рис.15.5,в).
(рис.15.5,б) і тільки в системі з комбінованим керуванням усталена похибка з часом стає рівною нулю (рис.15.5,в).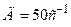 і
і  ?
? і
і  ?
?


