
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Часові та частотні характеристики двомасової системи
При сталих моментах інерції
Рис.2.8. Структурна схема двомасової системи електропривода
Перетворивши систему рівнянь (2.29) за Лампласом при нульових початкових умовах, одержимо
Цій системі рівнянь відповідає структурна схема на рис.2.8. Вона має на відміну від схеми на рис.2.4 перехрестні зворотні зв’язки. Для випадку
де Диференціальному рівнянню (2.30) відповідає характеристичне рівняння
де При З врахуванням визначених коефіцієнтів /2.31/ буде таким:
На рис.2.9. показано графік
Заміною в (2.33)
Амплітудночастотна характеристика двомасової системи
і фазочастотна характеристика
Оскільки З рис.2.10 слідує, що при
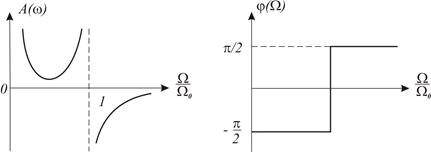
Рис.2.10. Амплітудночастотна та фазочастотна характеристики двомасової системи
Отже,
Контрольні запитання і задачі
1. Який закон використовують для виводу рівняння руху елект-ропривода? 2. Для яких виробничих механізмів справедливим є рівняння 3. Визначити час розгону електропривода до швидкості 4. Визначити час гальмування електропривода зі швидкості 5. Коли використовують грифо-аналітичний метод розрахунку часу розгону електропривода? 6. Запишіть рівняння передавальної функції електропривода за керуючим впливом, для якого 7. Запишіть рівняння амплітудночастотної характеристики елект-ропривода, для якого 8. Складіть рівняння руху двомасової системи електропривода. 9. У випадку 10. За якою формулою у двомасовій системі електропривода визначають власну частоту коливань?
Розділ 3
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.40.177 (0.008 с.) |

 Якщо між валом двигуна і робочим органом є пружна ланка, наприклад, довгий вал чи линва з коефі-цієнтом жорсткості
Якщо між валом двигуна і робочим органом є пружна ланка, наприклад, довгий вал чи линва з коефі-цієнтом жорсткості  , то таку сис-тему не можна привести до однома-сової. На рис.2.7
, то таку сис-тему не можна привести до однома-сової. На рис.2.7  – момент інерції двигуна і жорстко зв’язаних з ним мас;
– момент інерції двигуна і жорстко зв’язаних з ним мас;  – момент інерції робочого органа і жорстко зв’язаних з ним мас;
– момент інерції робочого органа і жорстко зв’язаних з ним мас; 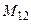 – пружний момент.
– пружний момент. ;
; ;
; . (2.29)
. (2.29)
 ;
;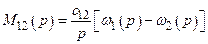 ;
; .
. і
і 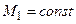 система рівнянь (2.29) при-водиться до виду:
система рівнянь (2.29) при-водиться до виду: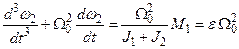 , (2.30)
, (2.30) і
і  .
. , корені якого
, корені якого  і
і  . Цим кореням відповідає розв’язок
. Цим кореням відповідає розв’язок , (2.31)
, (2.31)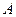 і
і 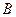 – коефіцієнти, які визначають із початкових умов.
– коефіцієнти, які визначають із початкових умов.
 і
і  , бо при
, бо при  дорівнює нулю. Підставивши в /2.31/
дорівнює нулю. Підставивши в /2.31/ 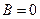 . Похідна
. Похідна 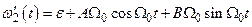 . Підставивши в це рівняння
. Підставивши в це рівняння 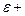
 . Звідси
. Звідси  .
. . (2.32)
. (2.32) і його складові згідно (2.32). З порівняння цього графіка з графіком на рис.2.1,а слідує, що пружна ланка зумовлює коливальну складову, яка має вид незгасаючих коливань. В реальній пружній ланці коливання є згасаючими, бо мають місце втрати енергії при деформації, що не було враховано при складанні рівнянь (2.29).
і його складові згідно (2.32). З порівняння цього графіка з графіком на рис.2.1,а слідує, що пружна ланка зумовлює коливальну складову, яка має вид незгасаючих коливань. В реальній пружній ланці коливання є згасаючими, бо мають місце втрати енергії при деформації, що не було враховано при складанні рівнянь (2.29). Рівнянню (2.30) відповідає передавальна функція
Рівнянню (2.30) відповідає передавальна функція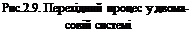
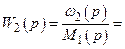
 . (2.33)
. (2.33)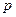 на
на  одержують амплітудно-фазову часто-тну характеристику
одержують амплітудно-фазову часто-тну характеристику . (2.34)
. (2.34)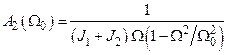 (2.35)
(2.35) . (2.36)
. (2.36) , то
, то 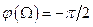 при
при  і
і 
 при
при  .
. амплітуда коливань стає рів-ною безмежності, що свідчить про виникнення явища резонансу.
амплітуда коливань стає рів-ною безмежності, що свідчить про виникнення явища резонансу. є частотою власних коливань системи. При
є частотою власних коливань системи. При  ?
?
 , якщо приведений момент інерції
, якщо приведений момент інерції  , момент
, момент  і момент сил опору
і момент сил опору 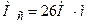 .
. ,якщо приведений момент інерції
,якщо приведений момент інерції  і момент сил опору
і момент сил опору 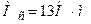 .
.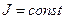 .
. . Для цього випадку скла-діть рівняння передавальної функції.
. Для цього випадку скла-діть рівняння передавальної функції.


