
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Безпошукова адаптивна система керування з еталонною
Моделлю
БАС з еталонною моделлю використовується в основному тоді, коли необхідно забезпечити бажані статичні і динамічні показники роботи системи при зміні її параметрів шляхом зміни параметрів регулятора (коефіцієнта підсилення, сталих часу чи формування додаткових впливів).
Рис. 14.1. Безпошукова адаптивна система з еталонною моделлю Зміну параметрів регулятора чи додаткові впливи здійснює блок адаптивного керування БАК, на вхід якого подаються вимірювані значення вхідної У складі БАК може бути пристрій, котрий оцінює недоступні вимірюванню змінні, наприклад, активний опір обмотки якоря чи ротора, і формує вихідний вплив
В якості еталонної моделі можна вибрати ланку другого порядку, яка буде описуватись диференціальним рівнянням
де
де
Вираз (14.2) називається 1-ю умовою реалізації закону У випадку комплексних коренів
і першу умову реалізації функції
де У випадку дійсних коренів (аперіодичний перехідний процес)
і умова (14.2) матиме вид:
де Коли
і
Електропривод таких виробничих механізмів як швидкісні ліфти, важкі верстати та інші повинен забезпечити не тільки обмеження моменту (прискорення), але і зміну прискорення – ривка, величи-ною
називається 2-ю умовою реалізації Для наведених на рис.14.3 кривих умови /14.9/ будуть такими: Ø для
де Ø для
(14.11) Ø для
Отримані формули для визначення допустимого моменту і ривка дозволяють не тільки перевірити умови реалізації адаптивного ке-рування, але і визначити
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.23.176 (0.007 с.) |

 і вихідної
і вихідної  величини.
величини.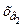 , величина і знак якого зале-жать від відхилення вихідної змінної
, величина і знак якого зале-жать від відхилення вихідної змінної  від вихідної змінної еталон-ної моделі
від вихідної змінної еталон-ної моделі  в установленому режимі.
в установленому режимі. Вихідний адаптивний вплив
Вихідний адаптивний вплив  спричиняє зміну параметрів ре-гулятора Р, а вплив
спричиняє зміну параметрів ре-гулятора Р, а вплив  .
. Якби не було БАК, то при зміні параметрів об’єкта керування перехідні процеси мо-гли бути з перерегулюванням (крива 2) чи без нього, але з великим часом регулювання (крива 3).
Якби не було БАК, то при зміні параметрів об’єкта керування перехідні процеси мо-гли бути з перерегулюванням (крива 2) чи без нього, але з великим часом регулювання (крива 3). , (14.1)
, (14.1)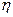 – коефіцієнт затухання;
– коефіцієнт затухання; 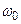 – власна частота коливань,
– власна частота коливань,  .
. При початкових умовах
При початкових умовах 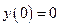 і
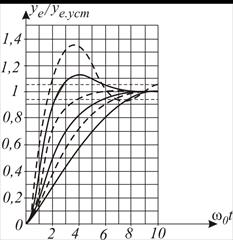
і  розв’язки (14.1) у відносних одиницях представлено сімейством кривих (рис. 14.3). Графічне представлення вихідної величини еталонної моделі
розв’язки (14.1) у відносних одиницях представлено сімейством кривих (рис. 14.3). Графічне представлення вихідної величини еталонної моделі 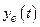 наглядно показує, до якої кривої необхідно наближати перехідний процес в адаптивній системі керування, і спрощує визначення коефіцієнтів рівняння (14.1) за вибраними
наглядно показує, до якої кривої необхідно наближати перехідний процес в адаптивній системі керування, і спрощує визначення коефіцієнтів рівняння (14.1) за вибраними  . При цьому усталене значення
. При цьому усталене значення
 ,
, – коефіцієнт підсилен-ня розімкненої системи з одиничним зворотним зв’язком. Вибравши еталонний перехідний процес, необхідно перевірити чи зможе його реалізувати двигун, момент якого завжди обмежений величиною
– коефіцієнт підсилен-ня розімкненої системи з одиничним зворотним зв’язком. Вибравши еталонний перехідний процес, необхідно перевірити чи зможе його реалізувати двигун, момент якого завжди обмежений величиною  за умови, що
за умови, що  . Очевидно, що максимальне значення розрахункового моменту
. Очевидно, що максимальне значення розрахункового моменту  , визначеного за кривою
, визначеного за кривою  . (14.2)
. (14.2)
 . Величину
. Величину  значення
значення  у точці
у точці  . Розв’язок (14.1) залежить від коренів характеристичного рівняння
. Розв’язок (14.1) залежить від коренів характеристичного рівняння  , які можуть бути комплексно-спряженими
, які можуть бути комплексно-спряженими 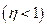 , кратними
, кратними  і дійсними
і дійсними  .
. (14.3)
(14.3) , (14.4)
, (14.4) – максимальний момент інерції електропривода;
– максимальний момент інерції електропривода;  .
. (14.5)
(14.5)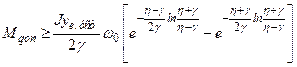 , (14.6)
, (14.6)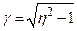 .
.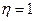 , то
, то (14.7)
(14.7) . (14.8)
. (14.8) . Тому величина
. Тому величина 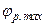 для вибраної
для вибраної 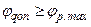 (14.9)
(14.9)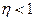
 , (14.10)
, (14.10) ;
;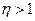
 ;
; (14.12)
(14.12)


