Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «Математичний та фізичний маятник»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Знати: уявлення про залежність періоду власних коливань від параметрів системи; взаємні перетворення кінетичної та потенціальної енергії матеріальної точки під час коливань; затухання коливань за наявності сил тертя і порушення закону збереження повної механічної енергії. Поняття: амплітуда, період, частота коливань, резонанс, поперечні й поздовжні хвилі, довжина хвилі. Уміти: вимірювати і робити розрахунки для визначення періоду коливань маятника ü План теоретичного матеріалу. 1) Математичний маятник. 2) Фізичний маятник. Теоретичний матеріал Математичний маятник
то рівноцінна
Оскільки залежність такої сили від кута <р нелінійна, то коливання маятника не будуть гармонічними. Для малих кутів <р можна записати, що
де І — довжина маятника. При такій умові вертальна сила пропорційна куту ф, тому коливання маятника можна вважати гармонічними. Рівняння руху математичного маятника має такий вигляд:
Знак "мінус" вказує на те, що вертальна сила напрямлена до положення рівноваги, а зміщення відраховується від положення рівноваги, тому знак прискорення протилежний знаку зміщення. Проводячи аналогію між рівняннями (10.12) і (10.27), можна записати, що Тоді з (10.14) маємо
Фізичний маятник Фізичним маятником називають тверде тіло, здатне здійснювати коливання навколо нерухомої горизонтальної осї, яка не проходить через центр мас (рис. 10.9). Зрозуміло, що у положенні рівноваги фізичного маятника його центр мас С знаходиться на вертикалі з точкою підвісу О, але нижче від неї. При відхиленні маятника від положення рівноваги на кут <р виникає обертальний момент М сили тяжіння, плече якої /' = І sin ср. Він намагається повернути маятник у положення рівноваги. Якщо дією моментів сил тертя нехтувати, то з основного рівняння динаміки обертального руху дістанемо рівняння руху фізичного маятника:
де І — момент інерції тіла відносно горизонтальної осі, що проходить через точку підвісу О (у даному разі вісь перпендикулярна до площини рисунка); т — маса маятника; знак "мінус" вказує на те, що повертаючий момент намагається повернути маятник до положення рівноваги, а кут відхилення ер від положення рівноваги відраховується у протилежному напрямі. Для малих кутів відхилення sin <р «ер, і рівняння (1,0.29) набуває вигляду
Перепишемо рівняння (10.30) у такій формі:
Підставивши у mgl/I одиниці т, g, І і /, дістанемо, що розмірність цього виразу дорівнює розмірності частоти у квадраті. Тому можна зробити таке позначення: mgl/I = coj. Тоді рівняння (10.31) за виглядом збігається з рівнянням (10.13), а величина <р буде змінюватися гармонічно з періодом
Порівнюючи формулу (10.32) з (10.28) доходимо висновку, що величина І/(ті) вимірюється в одиницях довжини, тобто
Величину L називають зведеною довжиною фізичного маятника. Очевидно математичний. маятник матиме такий самий період коливань, як і фізичний маятник, за умови, що його довжина дорівнює зведеній довжині фізичного маятника. Неважко показати, що L> І. Справді, за теоремою Гюйгенса — ІПтейнера момент інерції маятника відносно осі, що проходить через точку підвісу О, дорівнює
де Іо — момент інерції маятника відносно паралельної осі, що проходить через його центр мас. Тоді
Точку О', що міститься на лінії ОС на відстані L від точки підвісу О, називають точкою коливань, або центром коливань фізичного маятника. Якщо в цій точці підвісити фізичний маятник, то його період коливань не зміниться. Справді, якщо О' — точка підвісу маятника, то йото нова зведена довжинаО
Оскільки Маятники широко застосовуються у годинниках, у приладах для визначення прискорення рухомих тіл і вивчення коливань земної кори (сейсмографи), у гіроскопічних приладах, у приладах для експериментального визначення моментів інерції тіл для дослідження механічних властивостей твердих тіл при різних фізичних умовах тощо.
ü Задачі. ü Самостійно розв’язати задачі: ü Питання самоконтролю: 1. Вертальна сила. 2. Рівняння руху математичного маятника. 3. Період математичного маятника. 4. Основне рівняння динаміки обертального руху фізичного маятника. 5. Зведена довжина фізичного маятника. 6. Центр коливань фізичного маятника. Література: Посібник №1. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За ред. І.М. Кучерука. - [2-е вид., випр.] - К.: Техніка, 2006. - 532 с. - Т.1: Механіка. Молекулярна фізика і термодинаміка Посібник №2. Кучерук Ї.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За пр. І.М. Кучерука. – [2-е вид., ипр..] — К.: Техніка, 2006. – 452 с. – Т.2: Електрика і магнетизм. Посібник № 3. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За ред. І.М. Кучерука. - [2-е вид., зипр.] -К.: Техніка, 2006. - 518 с. - Т.З: Оптика. Квантова фізика. Посібник №4. П.П. Чолпан Основи фізики: навч. Посібник: - К. Вища шк., 1995.- 488 с.: іл. Посібник №5. І.П. Гаркуша, І.Т. Горбачук, В.П. Курінний та ін.; за заг. ред. І.П. Гаркуші./Загальний курс фізики: Зб. Задач./ К.Техніка,2003.-560с. Л1. Том1, частина1, розділ10, §10.4-10.5,с.219-220 Л5. Розділ 4, §4.2, с. 192 Самостійна робота №15
|
||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 844; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.148 (0.01 с.) |

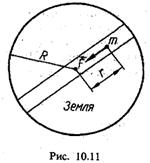
 Одним з найпростіших прикладів гармонічного коливання є коливальний рух математичного маятника. Математичним маятником називають матеріальну точку, підвішену на невагомій і неррзтяжній нитці, що коливається у вертикальній площині під дією сили тяжіння (рис. 10.8). До математичного маятника за своїми властивостями найбільше подібна система, що складається знерозтяжної легкої нитки, до одного з кінців якої підвішено металеву кульку. Можна вважати, що центр маси такої системи збігається з центром мас кульки. Коли система перебуває у спокої, то сила тяжіння зрівноважується силою натягу нитки
Одним з найпростіших прикладів гармонічного коливання є коливальний рух математичного маятника. Математичним маятником називають матеріальну точку, підвішену на невагомій і неррзтяжній нитці, що коливається у вертикальній площині під дією сили тяжіння (рис. 10.8). До математичного маятника за своїми властивостями найбільше подібна система, що складається знерозтяжної легкої нитки, до одного з кінців якої підвішено металеву кульку. Можна вважати, що центр маси такої системи збігається з центром мас кульки. Коли система перебуває у спокої, то сила тяжіння зрівноважується силою натягу нитки . Якщо кульку відхилити на деякий кут <р,
. Якщо кульку відхилити на деякий кут <р, сил натягу
сил натягу  і земного тяжіння Р намагається повернути кульку в положення рівноваги. Вертальна сила
і земного тяжіння Р намагається повернути кульку в положення рівноваги. Вертальна сила (10.25)
(10.25) , і вираз вертальної сили буде
, і вираз вертальної сили буде (10.26)
(10.26) (10.27)
(10.27)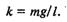
 (10.28)
(10.28) Звідси випливає, що період коливань математичного маятника не залежить від амплітуди коливань (для малих значень кута відхилень (р) і маси маятника, а визначається його довжиною і прискоренням вільного падіння тіл у даному місці Землі.
Звідси випливає, що період коливань математичного маятника не залежить від амплітуди коливань (для малих значень кута відхилень (р) і маси маятника, а визначається його довжиною і прискоренням вільного падіння тіл у даному місці Землі. (10.29)
(10.29) (10.30)
(10.30) (10.31)
(10.31) (10.32)
(10.32) (10.33)
(10.33)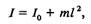

 (10.34)
(10.34) то з (10.34) маємо, що
то з (10.34) маємо, що  Отже, точка підвісу О фізичного маятника і його центр коливань О' є взаємними або спряженими. Ця властивість використовується в оборотних маятниках, які застосовуються для визначення з великою точністю прискорення вільного падіння у різних точках Землі.
Отже, точка підвісу О фізичного маятника і його центр коливань О' є взаємними або спряженими. Ця властивість використовується в оборотних маятниках, які застосовуються для визначення з великою точністю прискорення вільного падіння у різних точках Землі.