
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рух в'язкої рідини. В'язкість. Формуле ПуйэейляСодержание книги
Поиск на нашем сайте
На відміну від ідеальних рідин у реальних рідинах при русі одних шарів рідини відносно інших діють сили, дотичні ДО поверхонь дотикання шарів- Ці сили називають силами в'язкого тертя або силами &язкості. Уявно потік рідини можна поділити на нескінченну кількість шарін. При відносному переміщенні на кожний з шарів діють сили, 3 боку шару, швидкість якого більша, діє сила на шар, швидкість якого менша. Напрям, цієї сали збігається з напрямом руху рідини- 3 боку шару, швидкість руху якого менша, на шар, що рухається з більшою швидкістю, діє сила, яка напрямлена у протилежний бік від руху рідини, тобто вона цей шар гальмує.
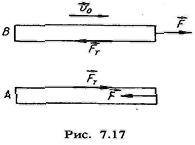
Для засування закономірностей, яким підлягають сили в'язкого тертя, розглянемо такий дослід. У рідині знаходяться дві пластини, лінійні розміри яких значно перевищують відстань між ними (рис. 7,17). Вважатимемо, що нижня пластина Л нерухома, а верхня пластина В рукається відносно нижньої зі швидкістю т?о. Для того щоб пластина В рухалася зі сталою швидкістю, на неї повинна діяти певна і:ила % Оскільки пластина рухається без прискорення, то на неї діє у протилежному напрямі до ovxy зрівноважуюча сила, яка є силою в'язкого тертя, тобто Ньютон експериментально встановив, що сила пропорційна площі пластини 5, швидкості v0 t обернено пропорційна відстані між, пластинами d, тобто
де ц — коефіцієнт пропорційності, який залежить від природи і стану рідини. Його називають динамічним коефіцієнтом внутрішнього тертя або коефіцієнтом в'язкості чи просто в'язкістю. Формула (7.21) справджується не тільки за умови, що одна з пластин перебуває в спокої, вона діє і тоді, коли обидві пластини рухаються рівномірно, але з різними швидкостями. Отже, формула (7.21) матиме вигляд
де V\ і Vi — відповідно швидкості верхньої і нижньої пластин. Величину, що дорівнює зміні швидкості на одиницю відстані між шарами, називають градієнтом швидкості і позначають qradV. Якщо напрям'осі ОХ перпендикулярний до рухомих шарів рідини, то градієнт швидкості
Тоді вираз (7.22) перепишемо так:
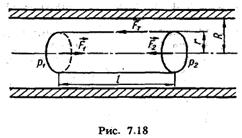
З цієї формули можна встановити фізичний зміст коефіцієнта в'язкості: ц = F при S = 1 і dv/dx = 1, тобто коефіцієнт в'язкості чисельно дорівнює силі, що діє на одиницю площі рухомих шарів рідини при градієнті швидкості рівному одиниці. Одиницею в'язкості в СІ є пас-каль-секунда (Па-с). Висловлені в цьому параграфі міркування однаковою мірою стосуються як рідин, так і газів. Відмінність виявляється лише в тому, що коефіцієнт в'язкості для рідин зменшується з підвищенням температури, а для газів, навпаки, зростає з підвищенням температури. Розглянемо стаціонарний потік рідини у горизонтальній циліндричній трубі сталого перерізу, радіус якої R. Знайдемо закон зміни швидкості із зміною відстані г від осі труби. Виділимо в трубі циліндричний об'єм рідини радіуса г і завдовжки І (рис. 7.18). Вісь симетрії циліндра збігається з віссю труби. На основи циліндра діють сили тиску, рівнодійна яких збігається з напрямом течії,
На бтщг поверхню циліндра діє сила тертя, яка на основі виразу (7.23) буде
де Для стаціонарного потоку
Оскільки швидкість руху рідини з віддаленням від осі труби зменшується, то
Звідси маємо
Проінтегрувавши цей вираз, маємо
Вираз (7 .29) набирає вигляду
Максимальну швидкість має рідина на осі труби, тобто
Отже, при віддаленні від осі труби швидкість & змінюється за параболічним законом. Визначимо об'єм рідини, що протікає через поперечний переріз труби за проміжок-.часу t. Уявно поперечний переріз труби поділимо на концентричні кільця, ширина яких dr (рис. 7.19). Площа кільця dS = 2nrdr. За час t через таке кільце протікає об'єм рідини
а за одиницю часу
Формулу (7.35) називають формулою Пуазейля. З цієї формули випливає, що об'єм рідини, яка протікає через трубу при сталому перепаді тисків, пропорційний четвертому степеню радіуса труби і обернено пропорційний довжині труби та в'язкості рідини. Формула справедлива тільки для ламінарних потоків рідини. Ламінарним називають такий потік, при якому частинки рідини рухаються вздовж прямолінійних траєкторій, паралельних юсі труби. Формулу Пуазейля покладено в основу експериментальних методів визначення в'язкості рідин та газів. До турбулентних потоків формула Пуазейля непридатна. Характер взаємодії між рідиною і тілом, що міститься у рідині, залежить від їхньої відносної швидкості. З механічного принципу відносності випливає, що сила взаємодії між ними однакова як для руху твердого тіла в нерухомій рідині, так і в разі обтікання нерухомого тіла рідиною, що рухається з такою самою за модулем і протилежною за напрямом швидкістю. Сила, з якою діє рідина на тіло при їхньому відносному русі, залежить також від форми тіла і в загальному випадку буде напрямлена під деяким кутом до напряму руху. Цю силу завжди можна розкласти на дві взаємно перпендикулярні складові сили. Складову, що діє у напрямі потоку, називають силою лобового опору. Складову, що перпендикулярна до напряму потоку, називають піднімальною силою. На симетричні тіла, вісь симетрії яких збігається з напрямом потоку, діє тільки сила лобового потоку. Вона залежить від форми та розмірів тіл, швидкості потоку рідини та від її властивостей. При обтіканні кулі потоком рідини лінії течії поблизу поверхні кулі зазнають симетричних викривлень. Відповідно до рівняння Бернуллі, розподіл тисків дубе симетричним і результуюча сила, що діє на поверхню кулі, дорівнюватиме нулю. Інша картина спостерігається при обтіканні тіл реальними речовинами, які мають в`язкість. Такі рідини не можуть вільно ковзати по поверхні тіла. У цьому разі досить тонкий шар рідини прилипає до поверхні тіла і утворює суміжний шар. Його відносна швидкість дорівнює нулю. З віддаленням від поверхні тіла швидкість руху шарів рідини зростає. Внаслідок наявності градієнтів швидкості руху рідини біля поверхні тіла на нього діятиме сила в`язкого тертя. Результуюча сила в`язкості, що діє на тіло, направлена вздовж потоку рідини. Дослід показує, що її величина пропорційна швидкості, тобто
де Оскільки попереду тіла тиск більший від тиску в області вихорів тіла на величину де Висновок: отже, на тіло у рухомій рідині діють сили в`язкості і лобового опору. Сили в`язкості діють на бічну поверхню тіла, сили лобового опору – на поверхню тіла, на яку набігає потік рідини. Останні виникають внаслідок того, що тіло, яке омивається рідиною, змінює імпульс її елементів, тобто діє з деякими силами на елементи рідини. Сили в`язкості і сили лобового опору завжди діють одночасно на тіла, розміщені у рухомій рідині. ü Задачі. ü Самостійно розв’язати задачі: ü Питання самоконтролю: 1. Коефіцієнт вязкості. Одиниця вязкості. 2. Формула Пуазейля. 3. Поняття ламінарної течії. Схема витікання рідини. 4. Турбулентний режим течії. 5. Фізичний зміст числа Рейнольдса. Література: Посібник №1. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За ред. І.М. Кучерука. - [2-е вид., випр.] - К.: Техніка, 2006. - 532 с. - Т.1: Механіка. Молекулярна фізика і термодинаміка Посібник №2. Кучерук Ї.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За пр. І.М. Кучерука. – [2-е вид., ипр..] — К.: Техніка, 2006. – 452 с. – Т.2: Електрика і магнетизм. Посібник № 3. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За ред. І.М. Кучерука. - [2-е вид., зипр.] -К.: Техніка, 2006. - 518 с. - Т.З: Оптика. Квантова фізика. Посібник №4. П.П. Чолпан Основи фізики: навч. Посібник: - К. Вища шк., 1995.- 488 с.: іл. Посібник №5. І.П. Гаркуша, І.Т. Горбачук, В.П. Курінний та ін.; за заг. ред. І.П. Гаркуші./Загальний курс фізики: Зб. Задач./ К.Техніка,2003.-560с. Л1.Том 1, частина 1, розділ 7, §7.4-7.5,с.162-167 Л5. Розділ 1, §1.6, с. 55 Самостійна робота №11
|
||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 1053; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.57 (0.011 с.) |

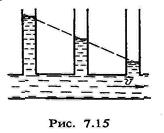
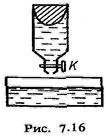
 Наявність сил в'язкості, одо діють у рухомій рідині, підтверджується дослідними даними. Так, при русі рідини у горизонтальній трубі сталого перерізу рівні рідини у манометричних трубках, за законом Бернуллі, повинні бути однакові. Насправді ж тиск рідини в трубі спадає у напрямі її руху (рис. 7Л5К Для того щоб рух рідини в трубі був стаціонарним, на її кінцях треба підтримувати сталу різницю тисків, сила яких зрівноважує сили внутрішнього тертя. Зовнішні сили при переміщенні рідіїни в трубі виконують роботу, яка йде на подолання сил в'язкого тертя. В'язке тертя у рухомій рідині значно ускладнює описання її руху. Так, при стаціонарному русі в нз-кої рідини швидкість течії в різних точках поперечного перерізу неоднакова. Шар рідини, що безпосередньо прилягає до стінок труби, прилипає до неї, залишаючись практично нерухомим, 3 віддаленням від стінок труби швидкість руху шарів рідини зростає. Це можна спостерігати нз такому досліді. У вертикальну скляну трубку наливають роду <рис. 7.16). Потім обережно наливають забарвлену воду, В стані спокою межа поділу горизонтальна. За допомогою крана К добиваються досить повільного витікання рідини. При цьому межа поділу з часом змінює свою форму» витягуючись вздовж осі трубки. Межа поділу набуває форми параболоїда обертання. Такий розподіл швидкостей у рухомій рідині зумовлений наявністю сил тертя між шарами рідини.
Наявність сил в'язкості, одо діють у рухомій рідині, підтверджується дослідними даними. Так, при русі рідини у горизонтальній трубі сталого перерізу рівні рідини у манометричних трубках, за законом Бернуллі, повинні бути однакові. Насправді ж тиск рідини в трубі спадає у напрямі її руху (рис. 7Л5К Для того щоб рух рідини в трубі був стаціонарним, на її кінцях треба підтримувати сталу різницю тисків, сила яких зрівноважує сили внутрішнього тертя. Зовнішні сили при переміщенні рідіїни в трубі виконують роботу, яка йде на подолання сил в'язкого тертя. В'язке тертя у рухомій рідині значно ускладнює описання її руху. Так, при стаціонарному русі в нз-кої рідини швидкість течії в різних точках поперечного перерізу неоднакова. Шар рідини, що безпосередньо прилягає до стінок труби, прилипає до неї, залишаючись практично нерухомим, 3 віддаленням від стінок труби швидкість руху шарів рідини зростає. Це можна спостерігати нз такому досліді. У вертикальну скляну трубку наливають роду <рис. 7.16). Потім обережно наливають забарвлену воду, В стані спокою межа поділу горизонтальна. За допомогою крана К добиваються досить повільного витікання рідини. При цьому межа поділу з часом змінює свою форму» витягуючись вздовж осі трубки. Межа поділу набуває форми параболоїда обертання. Такий розподіл швидкостей у рухомій рідині зумовлений наявністю сил тертя між шарами рідини.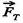 = —
= — 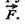 Виявляється, щоб нижня гхластина перебувала у спокої, до неї треба прикласти також силу
Виявляється, щоб нижня гхластина перебувала у спокої, до неї треба прикласти також силу  але протилежну за напрямом.
але протилежну за напрямом.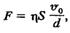 (7,21)
(7,21)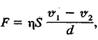 (7,22)
(7,22)
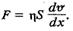 (7.23)
(7.23)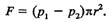 (7.24)
(7.24)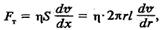 С7.25)
С7.25)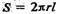 — площа бічної поверхні циліндра.
— площа бічної поверхні циліндра. , тобто
, тобто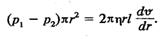 (7.26)
(7.26)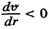 і рівняння (7.26) перепишемо так:
і рівняння (7.26) перепишемо так: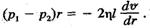 (7.27)
(7.27)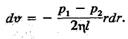 (7.28)
(7.28)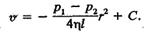 (7.29)
(7.29)
 Сталу інтегрування визначаємо з граничних умов. Для
Сталу інтегрування визначаємо з граничних умов. Для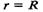
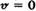 > тоді
> тоді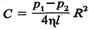
 (7.30)
(7.30) (7.31) Враховуючи вираз (7.31), формулу (7.30) можна записати
(7.31) Враховуючи вираз (7.31), формулу (7.30) можна записати (7.32)
(7.32)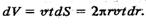 (7.33) Враховуючи (7.30), вираз (7.33) перепишемо у вигляді
(7.33) Враховуючи (7.30), вираз (7.33) перепишемо у вигляді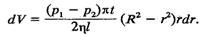 (7.34) Проінтегрувавши вираз (7.34), дістаємо
(7.34) Проінтегрувавши вираз (7.34), дістаємо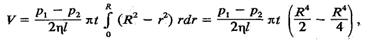
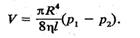 (7.35)
(7.35)
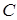 – коефіцієнт, який залежить від в`язкості рідини, розмірів і форми тіла, його орієнтації відносно потоку.
– коефіцієнт, який залежить від в`язкості рідини, розмірів і форми тіла, його орієнтації відносно потоку. , то сила лобового опору пропорційна густині рідини р, квадрату її відносної швидкості v та площі поперечного перерізу тіла S, тобто
, то сила лобового опору пропорційна густині рідини р, квадрату її відносної швидкості v та площі поперечного перерізу тіла S, тобто – коефіцієнт пропорційності, який залежить від числа Рейнольдса, форми тіла та його орієнтації у потоці рідини.
– коефіцієнт пропорційності, який залежить від числа Рейнольдса, форми тіла та його орієнтації у потоці рідини.


