ТОП 10:
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Обработка изделий медицинского назначения многократного применения Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пружні властивості реальних тіл. Енергія пружної деформації. Пружний гістерезис
Усі реальні тіла можна вважатя пружними тільки при досить малих деформаціях. Коли деформації перевищують деяку граничну величину, яка для різник тіл неоднакова, то властивості тіл значно відрізняються від властивостей абсолютно пружних тіл. Пружні властивості реальних тіл залежно від їхньої деформації Зручно вивчати за так званою діаграмою деформував на. Вона являє
Матеріали, для яких області текучості практично немає, називають крихкими {цегла, скло, фарфор та ін). При дальшому розтязі за точку D тіло знову чинить опір деформації. Максимальне напруження ast що виникає в тілі перед початком його руйнування, називають межею міцності. При вищих напруженнях в одному Із перерізів тіла йоге діаметр зменшується і утворюється шийка, в якій відбувається руйнування. Якщо при першому деформуванні тіла напруження було більшим за межу пружності, то після припинення дії зовнішньої сили тіло повертається в стан О'. Якщо повторно деформувати тіло, то межа пружності його збільшиться. Зростання межі пружності т^ія внаслідок його повторних деформацій називають зміцнюванням. Пружність і пластичність тіл залежать також від температури, тиску і ряду інших умов, в яких тіла перебувають. Так, сталь пружна при звичайних умовах і пластична при високих температурах і тисках; свинець пластичний при кімнатній температурі і стає пружним при низьких температурах. Характер деформації в тілі залежить також від часу дії зовнішньої сили. На рис. 5.12 показано криву залежності деформації від часу дії сталої сили. У момент прикладання сили швидко встановлюється деформація АВ, потім вона повільно зростає по кривій ВС. У момент припинення дії сили деформація різко зменшується на величину CD і потім повільно спадає по кривій DE, Це явище називають пружною післядією. Характер залежності Для деформації тіла треба, щоб прикладені до нього сили виконали роботу. В свою чергу, деформоване тіло здатне виконати роботу за рахунок енергії пружної деформації.
На основі формул (5.8) і (5.11) маємо
Робота цієї сили при зміні величини х від 0 до Д/ буде
Перепишемо цей вираз так:
де
Порівнюючи роботу, виконану зовнішніми силами, і потенціальну енергію деформованого стержня, вважаємо, що патендіальна енергій недеформованого стержня дорівнює нулю. Знайдемо об'ємну густину енергії пружної деформації, тобто енергію, що припадає на одиницю об'єму розтягнутого або стиснутого стержня: w = U / V. З (5-19) маємо
Аналогічно можна записати вираз для об'ємної густини енергії пружної деформації зсуву;
Якби до недеформованого тіла відразу прикласти силу F, то при видовженні стержня на АІ виконувалась би робота удвоє більша» тобто EVe2. Оскільки енергія пружної деформації дорівнює половині цієї роботи, то друга її половина витрачається на кінетичну енергію пружних коливань» які при цьому будуть збуджені у стержні,
При зменшенні зовнішньої сили до нуля робота пружної сили буде пропорційною площі фігури Якщо здійснити повний цикл деформації тіла, то робота зовнішньої сили за цикл буде пропорційна площі фігури- Робота пружної сили за той самий цикл буде пропорційною сумі площ фігур . Протягом циклу робота зовнішньої сили буде більшою від роботи пружної сили за той самий час на величину, що пропорційна площі фігури , яку називають петлею пружного гістерезису* Різниця цих робіт витрачається на подолання сил внутрішнього тертя в тілі і в результаті поповнює запас енергії молекул ярно-тсплового руху всередині тіла. Тому чим ширша для даного матеріалу петля гістерезису, тим більше нагрівається виготовлена з нього деталь при її періодичних деформаціях. Деталі машин, які зазнають швидких періодичних деформацій, виготовляють із спеціальних сортів сталі, для яких петля гістерезису досить вузька. ü Задачі. ü Самостійно розв’язати задачі: ü Питання самоконтролю: 1. За якої умови реальні тіла можна вважати пружними? 2. Межа пропорційності. Межа пружності. Межа текучості. Межа міцності. 3. Яке явище називають пружною післядією? 4. Сила. Робота сили. Енергія пружної деформації. 5. Об’ємна густина енергії. 6. Петля пружного гістерезісу.
Література : Посібник №1.Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За ред. І.М. Кучерука. - [2-е вид., випр.] - К.: Техніка, 2006. - 532 с. - Т.1: Механіка. Молекулярна фізика і термодинаміка Посібник №2. Кучерук Ї.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За пр. І.М. Кучерука. – [2-е вид., ипр..] — К.: Техніка, 2006. – 452 с. – Т.2: Електрика і магнетизм. Посібник № 3. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За ред. І.М. Кучерука. - [2-е вид., зипр.] -К.: Техніка, 2006. - 518 с. - Т.З: Оптика. Квантова фізика. Посібник №4. П.П. Чолпан Основи фізики: навч. Посібник: - К. Вища шк., 1995.- 488 с. : іл. Посібник №5.І.П. Гаркуша, І.Т. Горбачук, В.П. Курінний та ін.; за заг. ред. І.П. Гаркуші./Загальний курс фізики: Зб. Задач./ К.Техніка,2003.-560с. Л1. Том 1, частина 1, розділ 5, §5.4,с.120 Л5. Том1, Розділ 5, §5.4, с. 120 Самостійна робота №8 Тема: «Рухи планет. Закони Кеплера. Закон Всесвітнього тяжіння. Гравітаційна стала. Гравітаційна та інертна маси. Застосування законів збереження до руху тіл у центральному гравітаційному полі. Космічні швидкості» Знати: поняття сили тяжіння Уміти: обчислювати задачі на застосування законів Кеплера, Всесвітнього тяжіння, законів збереження до руху тіл, виведення значень космічних швидкостей ü План теоретичного матеріалу. 1. Рухи планет. Закони Кеплера. 2. Закон всесвітнього тяжіння. 3. Гравітаційна стала. 4. Гравітаційна та інертна маси. 5. Застосування законів збереження для руху тіл у центральному гравітаційному полі. 6. Космічні швидкості. Теоретичний матеріал |
||
|
Последнее изменение этой страницы: 2017-02-10; Нарушение авторского права страницы infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.80.55.37 (0.006 с.) |
собою графічну залежність між відносною деформацією розтяту є і механічним напруженням а, яку дістали експериментально. На рис. 5.11 зображено діаграму деформування для деформації розтягу металевого стержня. З цієї діаграми видно, що закон Гука виконується в досить вузьких межах зміни деформацій і напружень. Верхню межу напруження, при якій ще виконується лінійна залежність між в і сг, називають межен? пропорційності (е[3 о()г При напруженнях, які вищі за о, {від точки А до точки В {див. рис. 5ЛЇ)), деформація має ше пружний характер, але залежність між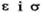 
нелінійна. Граничне напруження, при якому ще не виникає залишкова деформація, називають мех£ею пружності (є21 гтг}. За межами пружності в тілах виникають деформації, що зберігаються ї після припинення дії зовнішніх сил. Це так звана залишкова деформація. Тіло при припиненні дії зовніпініх сил повертається не в стан О, а в стан О'. Напруження, при якому виявляється помітна залишкова деформація {близько 0,2 %), називають межею текучості (точка С). За межею текучості при є > £2 ле жить область текучості. Для неї характерним є неперервне зростання деформації тіла з часом при майже сталому напруженні (ділянка CD),
, 
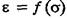дає можливість нетільки вибрати матеріал з необхідними властивостями при конструюванні різних установок і приладів, а й встановлювати зв'язок механічних властивостей тіл з їхньою структурою.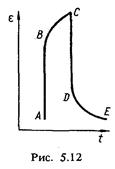
Ця енергія дорівнюватиме роботі пружних сил, якщо не відбувається зміна кінетичної енергії тіла. Для цього деформацію необхідно здійснювати досить повільно і зовнішні сили поступово збільшувати так, щоб у будь-який момент часу кожна частина тіла практично перебувала в стані рівноваги, тобто зовнішні сили весь час повинні зрівноважуватися пружними силами. Знайдемо енергію тіла при його деформації розтягу (стиску). Прикладемо до стержня силу F(x), яку будемо неперервно і повільно збільшувати від 0 до F. При цьому абсолютна деформація х змінюватиметься в межах від 0 до А/.
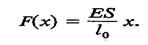(5.16)
(5.17)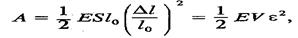
(5.18)
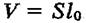— об'єм стержня. Тоді енергія пружної деформації розтягу
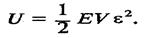(5.19)
<5.20)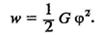
(5.21)
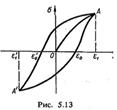Як уже зазначалося, коли механічні напруження досягають межі пружності (рис. 5.11), а потім зменшуються до нуля> то відносна деформація повністю не зникає, а зменшується до е0. При зміні деформації від 0 до е, зовнішні сили виконують роботу, величина якої пропорційна площі фігури ОА£,О на діаграмі розтягу (рис. 5.13). За рахунок цієї роботи виникає енергія пружної деформації При зменшенні деформації від е, до 0 пружні сили за рахунок енергії пружної деформації виконують роботу» величина якої пропорційна площі фігури Леое,А Якщо Змінити напрям дії сили і проводити деформацію у зворотному напрямі, досягши такого самого зна^ чення відносної деформації є',, то робота зовнішньої сили буде пропорційною площі фігури.