
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «межі руху і умови рівноваги системи в потенціальному полі. Абсолютно пружний і абсолютно не пружний удари »Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Знати: умови рівноваги системи та тіла Уміти: обчислювати задачі з використанням умов рівноваги ü План теоретичного матеріалу. 1. Закон збереження енергії. 2. Умови рівноваги системи. 3. Одномірний рух частинки в потенціальному полі сил. 4. Потенціальна крива руху частинки. 5. Удари тіл. Телретичний матеріал Закон збереження енергії. У прикладі, розібраному в попередньому параграфі, з'ясувалося, що зміна кінетичній енергії кинутого вгору тіла відбувається тільки за рахунок зміни його потенційній енергії і навпаки, так що сумарна механічна енергія тіла не міняється. Аналогічно, якщо на тіло діє стисла пружина, то вона може повідомити тілу деяку швидкість, тобто кінетичну енергію, але при цьому пружина розпрямлятиметься і її потенційна енергія відповідно зменшуватиметься; сума пружної енергії і кінетичної енергії залишиться постійною. Якщо на тіло, окрім пружини, діє ще і сила тяжіння, то хоча при русі тіла кількість енергії кожного виду змінюватиметься, але сума потенційної енергії тяжіння тіла, потенційній енергії пружності пружини і кінетичної енергії тіла знову-таки залишатиметься постійною. Енергія може переходити з одного вигляду в іншій, може переходити від одного тіла до іншого, але загальний запас механічної енергії залишається незмінним. Досліди і теоретичні розрахунки показують, що за відсутності сил тертя і при дії тільки сил пружності і тяжіння сумарна потенційна і кінетична енергія тіла або системи тіл залишається у всіх випадках постійною. У цьому і полягає закон збереження механічної енергії. Проілюструємо закон збереження енергії на наступному досвіді. Сталева кулька, падаюча з деякої висоти на сталеву або скляну плиту і що ударився об неї, підскакує майже на ту ж висоту, з якою впав. Під час руху кульки відбувається цілий ряд перетворень енергії. При падінні потенційна енергія тяжіння переходить в кінетичну енергію кульки. Коли кулька доторкнеться до плити, і він і плита починають деформуватися. Кінетична енергія перетворюється на потенційну енергію пружної деформації кульки і плити, причому цей процес продовжується до тих пір, поки кулька не зупиниться, тобто поки вся його кінетична енергія не перейде в потенційну енергію пружної деформації. Потім під дією сил пружності деформованої плити кулька набуває швидкості, направленої вгору: енергія пружної деформації плити і кульки перетворюється на кінетичну енергію кульки. При подальшому русі вгору швидкість кульки під дією сили тяжіння зменшується і кінетична енергія перетворюється на потенційну енергію тяжіння. У найвищій точці кулька володіє знову тільки потенційною енергією тяжіння. Оскільки можна вважати, що кулька піднялася на ту ж висоту, з якою він почав падати, потенційна енергія кульки на початку і в кінці описаного процесу одна і та ж. Більш того, у будь-який момент часу, при всіх перетвореннях енергії, сума потенційної енергії тяжіння, потенційній енергії пружності і кінетичної енергії весь час залишається однією і тією ж. Для процесу перетворення потенційної енергії, обумовленою силою тяжіння, в кінетичну і назад при падінні і підйомі кульки це було показано простим розрахунком в § 101. Можна було б переконатися, що і при перетворенні кінетичної енергії на пружну потенційну енергію плити і кульки і потім при зворотному процесі перетворення пружної енергії в кінетичну енергію відскакуючої кульки сума потенційної енергії тяжіння і пружності і кінетичної енергії також залишається незмінною, тобто закон збереження механічної енергії виконаний. Тепер ми можемо пояснити, чому порушувався закон збереження роботи в простій машині, яка деформувалася при передачі роботи (§ 95): річ у тому, що робота, витрачена на одному кінці машини, частково або повністю витрачалася на деформацію найпростішої машини (важеля, мотузка і т. д.), створюючи в ній деяку потенційну енергію деформації, і лише залишок роботи передавався на інший кінець машини. В сумі ж передана робота разом з енергією деформації виявляється рівній витраченій роботі. У разі абсолютної жорсткості важеля, нерозтяжності мотузка і т.д. проста машина не може накопичити в собі енергію, і вся робота, проведена на одному її кінці, передається на інший кінець без зміни. Тоді знаходимо: u1=v2, u2=v1 тобто кулі обмінюються швидкостями. Зокрема, якщо куля соударяется з нерухомою кулею рівної маси, то вона повідомляє йому свою швидкість, а сам зупиняється. Якщо маса однієї кулі значно більше маси іншої кулі, наприклад, якщо т1 багато більше m2, то, як видно з формули (102.5), і в знаменнику і в чисельнику можна нехтувати членами, m2, що містять. Якщо, крім того, масивна куля покоїться, то одержуємо u2= =— v2 тобто куля відскакує, як від нерухомої стінки. Дійсно, як видно з (102.4), велика куля одержить при цьому малу швидкість, рівну приблизно
Проілюструємо закон збереження енергії на наступному досвіді. Сталева кулька, падаюча з деякої висоти на сталеву або скляну плиту і що ударився об неї, підскакує майже на ту ж висоту, з якою впав. Під час руху кульки відбувається цілий ряд перетворень енергії. При падінні потенційна енергія тяжіння переходить в кінетичну енергію кульки. Коли кулька доторкнеться до плити, і він і плита починають деформуватися. Кінетична енергія перетворюється на потенційну енергію пружної деформації кульки і плити, причому цей процес продовжується до тих пір, поки кулька не зупиниться, тобто поки вся його кінетична енергія не перейде в потенційну енергію пружної деформації. Потім під дією сил пружності деформованої плити кулька набуває швидкості, направленої вгору: енергія пружної деформації плити і кульки перетворюється на кінетичну енергію кульки. При подальшому русі вгору швидкість кульки під дією сили тяжіння зменшується і кінетична енергія перетворюється на потенційну енергію тяжіння. У найвищій точці кулька володіє знову тільки потенційною енергією тяжіння. Оскільки можна вважати, що кулька піднялася на ту ж висоту, з якою він почав падати, потенційна енергія кульки на початку і в кінці описаного процесу одна і та ж. Більш того, у будь-який момент часу, при всіх перетвореннях енергії, сума потенційної енергії тяжіння, потенційній енергії пружності і кінетичної енергії весь час залишається однією і тією ж. Для процесу перетворення потенційної енергії, обумовленою силою тяжіння, в кінетичну і назад при падінні і підйомі кульки це було показано простим розрахунком в § 101. Можна було б переконатися, що і при перетворенні кінетичної енергії на пружну потенційну енергію плити і кульки і потім при зворотному процесі перетворення пружної енергії в кінетичну енергію відскакуючої кульки сума потенційної енергії тяжіння і пружності і кінетичної енергії також залишається незмінною, тобто закон збереження механічної енергії виконаний. Тепер ми можемо пояснити, чому порушувався закон збереження роботи в простій машині, яка деформувалася при передачі роботи (§ 95): річ у тому, що робота, витрачена на одному кінці машини, частково або повністю витрачалася на деформацію найпростішої машини (важеля, мотузка і т. д.), створюючи в ній деяку потенційну енергію деформації, і лише залишок роботи передавався на інший кінець машини. В сумі ж передана робота разом з енергією деформації виявляється рівній витраченій роботі. У разі абсолютної жорсткості важеля, нерозтяжності мотузка і т.д. проста машина не може накопичити в собі енергію, і вся робота, проведена на одному її кінці, передається на інший кінець без зміни. Користуючись двома «законами збереження»: законом збереження імпульсу і законом збереження енергії, можна вирішити завдання про зіткнення ідеально пружних куль, тобто куль, які після зіткнення відскакують один від одного, зберігаючи сумарну кінетичну енергію. Хай дві кулі рухаються по одній прямій (лінії центрів). Припустимо, що, окрім сил взаємодії при їх зіткненні, на кулі не діють ніякі сили з боку яких-небудь інших тіл. Після зіткнення (зіткнення відбудеться, якщо кулі рухаються назустріч один одному або якщо один з них наздоганяє другий) вони рухатимуться по тій же прямій, але із зміненими швидкостями. Вважатимемо, що нам відомі маси куль т1 та тг і їх швидкості v1 и vг до зіткнення. Потрібно знайти їх швидкості v1 и vг після зіткнення. Із закону збереження імпульсу виходить, що, зважаючи на те що на кулі не діють ніякі сили, окрім сил їх взаємодії, сумарний імпульс повинен зберігатися, тобто імпульс до зіткнення повинен дорівнювати імпульсу після зіткнення:
Далі, з умови ідеальної пружності куль виходить, що зберігається також кінетична енергія куль, тобто повинна виконуватися рівність
З рівнянь (102.1) і (102.2) можна знайти дві невідомі швидкості і, і иг.. Насправді, перепишемо ці рівняння у вигляді
Ділячи почленно друге рівняння на перше, знаходимо:
Умножаючи (102.3) на m2 віднімаючи з (102.1), одержимо:
звідки знайдемо:
Подібним же чином, умножаючи (102.3) на m1 і складаючи з (102.3), знайдемо:
ü Задачі. ü Самостійно розв’язати задачі: ü Питання самоконтролю: 1. Приклад одномірного руху частинки. 2. Умови рівноваги частинки в потенціальному полі. 3. Потенціальний бар’єр. 4. Удар тіл. Фізичні явища, що супроводжують удари. Типи ударів. 5. Абсолютно пружний удар. 6. Абсолютно непружний удар. 7. Середня потужність удару. 8. Приклади абсолютно пружного удару двох куль. Закони збереження імпульсу і кінетичної енергії у замкненій системі двох куль(маси куль однакові, друга куля нерухома). 9. Приклад абсолютно непружного удару куль. 10. Практичні висновки. Література: Посібник №1. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За ред. І.М. Кучерука. - [2-е вид., випр.] - К.: Техніка, 2006. - 532 с. - Т.1: Механіка. Молекулярна фізика і термодинаміка Посібник №2. Кучерук Ї.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За пр. І.М. Кучерука. – [2-е вид., ипр..] — К.: Техніка, 2006. – 452 с. – Т.2: Електрика і магнетизм. Посібник № 3. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За ред. І.М. Кучерука. - [2-е вид., зипр.] -К.: Техніка, 2006. - 518 с. - Т.З: Оптика. Квантова фізика. Посібник №4. П.П. Чолпан Основи фізики: навч. Посібник: - К. Вища шк., 1995.- 488 с.: іл. Посібник №5. І.П. Гаркуша, І.Т. Горбачук, В.П. Курінний та ін.; за заг. ред. І.П. Гаркуші./Загальний курс фізики: Зб. Задач./ К.Техніка,2003.-560с. Л1.Том1. Частина 1, розділ 3, §3.6-3.7,с.79-81 Л5. Розділ 1, §1.4, с. 41 Самостійна робота №5
|
||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 635; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |


 Закон збереження енергії. У прикладі, розібраному в попередньому параграфі, з'ясувалося, що зміна кінетичній енергії кинутого вгору тіла відбувається тільки за рахунок зміни його потенційній енергії і навпаки, так що сумарна механічна енергія тіла не міняється. Аналогічно, якщо на тіло діє стисла пружина, то вона може повідомити тілу деяку швидкість, тобто кінетичну енергію, але при цьому пружина розпрямлятиметься і її потенційна енергія відповідно зменшуватиметься; сума пружної енергії і кінетичної енергії залишиться постійною. Якщо на тіло, окрім пружини, діє ще і сила тяжіння, то хоча при русі тіла кількість енергії кожного виду змінюватиметься, але сума потенційної енергії тяжіння тіла, потенційній енергії пружності пружини і кінетичної енергії тіла знову-таки залишатиметься постійною. Енергія може переходити з одного вигляду в іншій, може переходити від одного тіла до іншого, але загальний запас механічної енергії залишається незмінним. Досліди і теоретичні розрахунки показують, що за відсутності сил тертя і при дії тільки сил пружності і тяжіння сумарна потенційна і кінетична енергія тіла або системи тіл залишається у всіх випадках постійною. У цьому і полягає закон збереження механічної енергії.
Закон збереження енергії. У прикладі, розібраному в попередньому параграфі, з'ясувалося, що зміна кінетичній енергії кинутого вгору тіла відбувається тільки за рахунок зміни його потенційній енергії і навпаки, так що сумарна механічна енергія тіла не міняється. Аналогічно, якщо на тіло діє стисла пружина, то вона може повідомити тілу деяку швидкість, тобто кінетичну енергію, але при цьому пружина розпрямлятиметься і її потенційна енергія відповідно зменшуватиметься; сума пружної енергії і кінетичної енергії залишиться постійною. Якщо на тіло, окрім пружини, діє ще і сила тяжіння, то хоча при русі тіла кількість енергії кожного виду змінюватиметься, але сума потенційної енергії тяжіння тіла, потенційній енергії пружності пружини і кінетичної енергії тіла знову-таки залишатиметься постійною. Енергія може переходити з одного вигляду в іншій, може переходити від одного тіла до іншого, але загальний запас механічної енергії залишається незмінним. Досліди і теоретичні розрахунки показують, що за відсутності сил тертя і при дії тільки сил пружності і тяжіння сумарна потенційна і кінетична енергія тіла або системи тіл залишається у всіх випадках постійною. У цьому і полягає закон збереження механічної енергії.



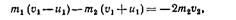
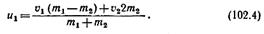
 Особливо спрощується співвідношення швидкостей при зіткненні куль однакової маси m1=m2
Особливо спрощується співвідношення швидкостей при зіткненні куль однакової маси m1=m2


