
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «додавання коливань одного напрямку, биття»
Знати: залежності періоду власних коливань від параметрів системи Уміти: розв’язувати задачі на визначення періоду коливань, довжини хвилі. ü План теоретичного матеріалу. 1. Додавання коливань одного напрямку. Биття. Теоретичний матеріал Додавання коливань однакового напряму. Биття Можливі випадки, коли тіло бере участь одночасно у кількох коливальних рухах. Так, кулька, підвішена па пружині у каюті корабля, здійснюватиме коливання у вертикальному напрямі. Кільове хитання корабля також змушує тіло коливатися у вертикальному напрямі. Результуюче зміщення тіла, що бере участь у кількох коливальних рухах, становить геометричну суму незалежних зміщень, акі тіло дістає у кожному колива л ьщлгіу русі зокрема. Знайдемо рівняння руху тіла, яке бере участь однО'Йсно у двох однаково напрямлених коливальних рухах з однаковими частотами:
Якщо тіло одночасно бере участь у двох коливальних рухах, що відбуваються вздовж однієї і тієї самої прямої, то його результуючий рук відбуватиметься також вздовж тієї самої прямої, Гіри цьому будемо користуватися методом векторних діаграм (рис. 10-12). Результуюче зміщення тіла у будь-який момент часу дорівнює сумі незалежних зміщень, тобто х = х, + х2. Оскільки вектори
де ^4 — амплітуда результуючого коливання; ф — початкова фаза. З рве. 10.12 маємо
З (10-37) видно, що амплітуда результуючого коливання залежить від різниці фаз складових коливань. Якщо то А = At +- А2. Коли
де Еі і Ег — енергії складових коливань. З (10.39) видно, що повна енергія результуючого коливання також залежить від різниці початкових фаз складових коливань. Розглянемо випадок додавання однаково напрямлених коливань з різними частотами, рівняння яких
Якщо вектори складових амплітуд
Звідси видно, що амплітуда результуючого коливання періодично змінюється за абсолютною величиною з часом, тобто
У зв'язку з тим що період модуля косинуса дорівнює п, період зміни амплітуди
У випадку, коли частоти коливань со, і в>2 близькі за величинами, виникає явище, яке називають биттям. У цьому разі со, — о>2 «со, + со2, і результуючий рух можна розглянути як періодичне коливання з пульсуючою амплітудою. Частота таких коливань дорівнює середньому арифметичному значенню частот складових коливань. На рис. 10.13, а показано залежність зміщення х з часом протягом періоду та зміни амплітуди результуючого коливання, що його дістали додаванням однаково напрямлених коливань. Амплітуди складових коливань однакові, а їхні частоти со, і со2 близькі за величиною (рис. 10.13. б). ü Задачі. ü Самостійно розв’язати задачі: ü Питання самоконтролю: 1. Рівняння коливного руху тіла. 2. Результуюче зміщення. 3. Результуюча амплітуда. 4. Період зміни амплітуди. 5. Биття Література: Посібник №1. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За ред. І.М. Кучерука. - [2-е вид., випр.] - К.: Техніка, 2006. - 532 с. - Т.1: Механіка. Молекулярна фізика і термодинаміка Посібник №2. Кучерук Ї.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За пр. І.М. Кучерука. – [2-е вид., ипр..] — К.: Техніка, 2006. – 452 с. – Т.2: Електрика і магнетизм.
Посібник № 3. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: У 3-х т. / За ред. І.М. Кучерука. - [2-е вид., зипр.] -К.: Техніка, 2006. - 518 с. - Т.З: Оптика. Квантова фізика. Посібник №4. П.П. Чолпан Основи фізики: навч. Посібник: - К. Вища шк., 1995.- 488 с.: іл. Посібник №5. І.П. Гаркуша, І.Т. Горбачук, В.П. Курінний та ін.; за заг. ред. І.П. Гаркуші./Загальний курс фізики: Зб. Задач./ К.Техніка,2003.-560с. Л1.Том 1, частина 1, розділ 10, §10.6,с.223 Л5. Розділ 4, §4.1, с. 188 Самостійна робота №16
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 693; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.32.213 (0.006 с.) |
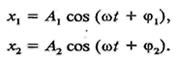 <10.35>
<10.35>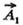 і
і  здійснюють обертання з однаковими кутовими швидкостями to, то зсув фаз між ними ч>2 — ф( з часом не змініоється, і вектор
здійснюють обертання з однаковими кутовими швидкостями to, то зсув фаз між ними ч>2 — ф( з часом не змініоється, і вектор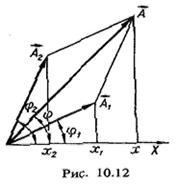 А також обертатиметься з кутовою швидкістю щ. Тоді результуюче коливання буде також гармонічним, і його рівняння ма тиме вигляд
А також обертатиметься з кутовою швидкістю щ. Тоді результуюче коливання буде також гармонічним, і його рівняння ма тиме вигляд (10.36)
(10.36)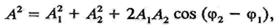 :; 00,37)
:; 00,37)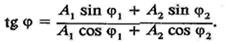 (10,33)
(10,33)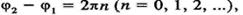
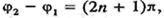 тобто складові коливання відбуваються у протилежник фазах, то амплітуда результуючого коливання А — \А^ — Аі І > бо за означенням амплітуда — величииа додатна. Оскільки енергія коливального руху пропорційна квадрату амплітуди, то повна енергія результуючого коливання
тобто складові коливання відбуваються у протилежник фазах, то амплітуда результуючого коливання А — \А^ — Аі І > бо за означенням амплітуда — величииа додатна. Оскільки енергія коливального руху пропорційна квадрату амплітуди, то повна енергія результуючого коливання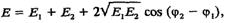 (10.39)
(10.39)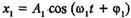
 (10.40)
(10.40)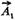 і
і 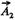 обертатимуться з різними кутовими швидкостями (рис. 10.12), то кут між ними змінюватиметься з часом і результуюча амплітуда також змінюватиметься з часом, тобто коливання буде негармонічним. Результуюче зміщення х = х, + х2. Дл£ спрощення припустимо, що
обертатимуться з різними кутовими швидкостями (рис. 10.12), то кут між ними змінюватиметься з часом і результуюча амплітуда також змінюватиметься з часом, тобто коливання буде негармонічним. Результуюче зміщення х = х, + х2. Дл£ спрощення припустимо, що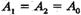
 . Тоді
. Тоді (10.41) Вираз (10.41) описує періодичні коливання з середньою частотою (о>, + й>2)/2 і модульованою амплітудою зміщення 2Ад. (Модуляція — це зміна за заданим законом з часом параметрів, що характеризують будь-який стаціонарний процес. Прикладом може бути зміна за певним законом амплітуди, частоти або фази гармонічних коливань.) Амплітуда змінюється від 0 до 2Ад за законом косинуса з набагато меншою частотою (ю2 - tBt)/2, яка дорівнює половині різниці частот складових коливань.
(10.41) Вираз (10.41) описує періодичні коливання з середньою частотою (о>, + й>2)/2 і модульованою амплітудою зміщення 2Ад. (Модуляція — це зміна за заданим законом з часом параметрів, що характеризують будь-який стаціонарний процес. Прикладом може бути зміна за певним законом амплітуди, частоти або фази гармонічних коливань.) Амплітуда змінюється від 0 до 2Ад за законом косинуса з набагато меншою частотою (ю2 - tBt)/2, яка дорівнює половині різниці частот складових коливань.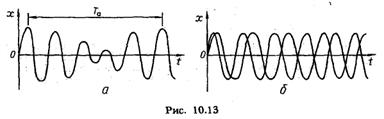
 (10.42)
(10.42)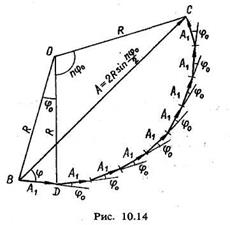
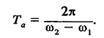 (10.43)
(10.43)


