Взаємозв'язок маси і енергії
Похожие статьи вашей тематики
Знайдемо вираз для кінетичної енергії W релятивістської частинки* Як і в нерелятивістській механіці, величину W означатимемо, яквеличину, приріст якої на певному відрізку траєкторії дорівнює роботі, виконаній над частинкою силою на цьому самому відрізку траєкторії.
Для елементарного переміщення 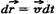 маємо маємо
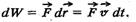 (9.29) З основного рівняння релятивістської динаміки (9.23) випливає, що (9.29) З основного рівняння релятивістської динаміки (9.23) випливає, що
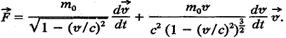
Враховуючи це співвідношення, вираз (9.29) запишемо так:

Оскільки 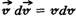 , а , а  , то , то
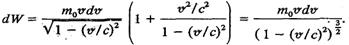 (9.30) Диференціюючи співвідношення (9.24), дістанемо (9.30) Диференціюючи співвідношення (9.24), дістанемо
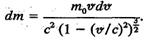 (9.31) (9.31)
На основі (9.31) рівність (9.30) можна переписати так:
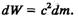 (9.32) (9.32)
Оскільки кінетична енергія частинки, яка перебуває у спокої, орівнює нулю, а її маса —т0, то, інтегруючи рівняння (9.32) в межах
двід 0 до Г і від га0 до т, дістанемо
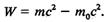 (9.33) Вираз (9.33) можна записати також як (9.33) Вираз (9.33) можна записати також як
 (9.34) (9.34)
: де 
 Формула (9.34) виражає кінетичну енергію релятивістської частинки. Цей вираз відрізняється від нерелятивістського Формула (9.34) виражає кінетичну енергію релятивістської частинки. Цей вираз відрізняється від нерелятивістського  , і його неможна подати-у вигляді , і його неможна подати-у вигляді 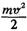 , де т – релятивістська маса частинки. , де т – релятивістська маса частинки.
. Розглянемо випадок малих швидкостей 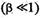 . Розкладемо вираз . Розкладемо вираз
  , користуючись формулою бінома, в ряд: , користуючись формулою бінома, в ряд:
Обмежуючись першими двома доданками ряду, матимемо
аким чином, при малих швидкостях вираз (9.34) перетворюється у нерелятивістський. На
рис. 9.8 для наочного порівняння зображено графіки залежності. Особливою є відмінність у значеннях WpM і WBep при швидкостях, близьких до швидкості світла
З формули (9.32) випливає, що приріст кінетичної енергії частинки має внутрішній нерозривний зв'язок з приростом її релятивістської маси. Враховуючи те, що різні види енергії їіожуть переходити з одного виду в інший, маса тіла може збільшуватися не тільки при зростанні його кінетичної енергії, а й при довільному зростанні інших видів енергії. На цій основі Ейнштейн зробив висновок: повна енергія тіла пов'язана з масою цього тіла співвідношенням
 (9.35) (9.35)
Формула (9.35) виражає один з фундаментальних законів природи — закон взаємозв'язку маси і енергії.
Вираз (9.35) з урахуванням (9.33) можна подати в іншій формі:
 (9.36) При v = 0 дістаємо (9.36) При v = 0 дістаємо
 (9Г37) (9Г37)
' де Ео — енергія спокою, або власна енергія тіла масою /ио.
Зміна повної енергії тіла ЛЄ супроводиться відповідно зміною його маси  і навпаки. і навпаки.
Закон взаємозв'язку маси і енергії особливо проявляється в ядерній фізиці і фізиці елементарних частинок, де розглядаються специфічні ядерні процеси і процеси перетворення елементарних частинок, які супроводяться великими змінами енергії порівняно з енергією спокою частинок.
Встановимо зв'язок енергії з імпульсом у рамках релятивістської механіки. Енергія тіла (частинки) і його імпульс пов'язані з релятивістською масою  співвідношеннями співвідношеннями 
де v — швидкість тіла. Піднесемо обидва рівняння до квадрата і друге рівняння домножимо на  : :

Віднімаючи від першого рівняння друге, дістанемо

або

Шуканий зв'язок між енергією та імпульсом має вигляд
 (9.38) (9.38)
Різниця 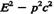 є інваріантною відносно перетворень Лоренца. є інваріантною відносно перетворень Лоренца.
З рівняння (9.38) для релятивістської енергії маємо
 (9.39) (9.39)
З рівності (9.39) випливає, що релятивістська енергія властива та-^ісрж частинкам, які не мають маси спокою (т0 = 0). Такою частиною, наприклад, є фотон, енергія якого
 (9.40) а імпульс (9.40) а імпульс
 (9.41) (9.41)
Рівність (9.41) означає, що потік фотонів повинен чинити тиск. Світловий тиск вперше експериментально виміряв П. М. Лебедев.
Тиском світла пояснюється наявність хвостів у комет, структура планетарних туманностей.
|