
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторна робота № 4. 3. Непружний удар тілСодержание книги
Поиск на нашем сайте
МЕТА РОБОТИ: вивчення законів збереження механічної енергії та імпульсу. ПРИЛАДИ: два металевих циліндри підвішені на легких стержнях, кутова шкала.
Коротка теорія непружного удару
Ударом називається процес кінцевої зміни швидкостей тіл за відносно короткий час їх взаємодії. При абсолютно непружному ударі має місце абсолютно пластична деформація, коли набуті при деформації форма і розміри тіл повністю зберігаються після припинення дії сил. Кінетична енергія руху тіл перетворюється частково в тепло і частково в кінетичну енергію. Система замкнута (робота зовнішніх сил дорівнює нулю) і дисипативна. В таких системах виконується закон збереження імпульсу, а закон збереження механічної енергії не виконується, так як чістина її перетворюється в немеханічну енергію – тепло. Але закон збереження усіх видів енергії для замкнутих систем виконується
Рисунок 12.1
Розглянемо непружний центральний удар (рис. 12.1). Після удару тіла рухаються як одне ціле, тобто швидкість U обох тіл після удару однакова. Запишемо рівняння збереження імпульсу та енергії, прийнявши до уваги, що при пластичній деформації виділяється тепло Q:
При відомих масах тіл m1 і m2 та швидкостях u1 і u2 перед ударом знайдемо швидкость U після удару та кількість теплоти Q.
Наслідок: Якщо маси тіл однакові і одне із тіл, наприклад друге, не рухається, то після удару U = 0,5u, тобто швидкість тіл зменшиться в два рази, а в тепло перетвориться половина початкової кінетичної енергії
У роботі розглядається непружний удар двох тiл однакової маси, які пiдвiшені на стержнях (рис. 12.2). Кути відхилення стержнів вимірюються по шкалі. Маси тіл M і стержнів m, а також довжини стержнів L однакові.
Рисунок 12.2
При відхиленні стержня з вантажем на кут φ центр ваги тіла піднімається на Н, а стержня на Н/2. Їхня потенціальна енергія зростає на величину
В момент проходження тілом нижнього положення, тобто перед ударом ця потенціальна енергія, у відповідності із законом збереження механічної енергії, (якщо знехтувати опором повітря та силою тертя у підвісі), перетвориться у кінетичну енергію обертання перед ударом
Тут J – сума моментів інерції вантажу ML2 (як матеріальної точки) і стержня
Прирівнюючи праві частини рівнянь (12.6) і (12.7), знайдемо швидкість в залежності від кута відхилення
Після удару тіла рухаються як одне ціле. Тому, щоб знайти швидкість U та кінетичну енергію Е після удару, у формулах (12.7) і (12.8) М і m замінемо відповідно на 2М і 2m, а кут φ на кут β відхилення після удару
Відносна втрата механічної енергії на тепло із (12.7) ÷ (12.10)
Порядок виконання роботи
1. Розрахувати початковий кут відхилення φ = 15+3N у градусах. для першої половини групи, або φ = 3N для другої половини групи. N – номер підгрупи студентів. 2. Для забезпечення непружного характеру удару на контактуючих поверхнях тіл із пластиліну сформувати невеличку гірку. 3. Відхилити один із стержнів на розрахований кут φ і відпустити. По шкалі кутів зафіксувати кут відхилення β після удару. 4. Повторити п.3 ще чотири рази (всього буде 5), слідкуючи, щоб після удару тіла за рахунок деформації пластиліну злипались. Результати вимірювань занести в таблицю 12.1.
Таблиця 12.1
5. Розрахувати величини, вказані в таблиці, а також похибку Δβ вимірювання кута β. 6. За формулою (12.11) знайти відносну втрату механічної енергії, одержану експериментально. При виконанні закону збереження енергії вона повинна дорівнювати теоретичному значенню 0,5 (див. наслідок). 7. Порівняти значення 8. Зробити висновок щодо виконання законів збереження імпульсу та енергії. Контрольні запитання 1. Що називається ударом? 2. Який удар називається абсолютно пластичним? 3. Які системи називаються замкнутими? 4. Сформулювати закон збереження імпульсу. 5. Сформулювати закон збереження механічної енергії. 6. Записати закон збереження імпульсу для центрального абсолютно непружного удару куль.
7. Записати закон збереження механічної енергії для центрального абсолютно непружного удару куль. 8. Вивести формули для визначення швидкостей куль після абсолютно непружного удару.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.89.2 (0.007 с.) |


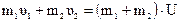 , (12.1)
, (12.1)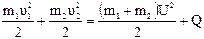 . (12.2)
. (12.2) , (12.3)
, (12.3)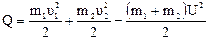 . (12.4)
. (12.4) . (12.5)
. (12.5)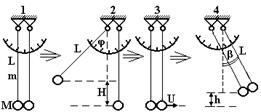
 .(12.6)
.(12.6)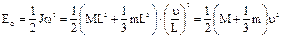 . (12.7)
. (12.7)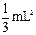 відносно точки підвісу;
відносно точки підвісу;  – кутова швидкість обертання; u – швидкість вантажу перед ударом.
– кутова швидкість обертання; u – швидкість вантажу перед ударом.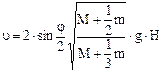 . (12.8)
. (12.8)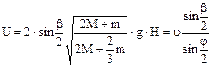 . (12.9)
. (12.9) . (12.10)
. (12.10) . (12.11)
. (12.11)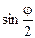


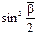
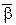 =
=
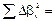

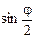 і 2
і 2 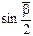 . Якщо закон збереження імпульсу виконується, то, згідно з (12.9) та наслідком, вони повинні бути однаковими.
. Якщо закон збереження імпульсу виконується, то, згідно з (12.9) та наслідком, вони повинні бути однаковими.


