
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спосіб логарифмування в економічному аналізіСодержание книги
Поиск на нашем сайте
Спосіб логарифмування застосовується для вимірювання впливу факторів у мультиплікативних моделях. Як і при інтегруванні, тут результат розрахунку також не залежить від місця розташування факторів у моделі. У порівнянні з інтегральним методом логарифмування забезпечує більш високу точність розрахунків. Якщо при інтегруванні додатковий приріст від взаємодії факторів розподіляється нарівно між ними, то за допомогою логарифмування результат спільної дії факторів розподіляється пропорційно частці ізольованого впливу кожного фактора на рівень результативного показника. У цьому його перевага, а недолік – в обмеженості сфери застосування. На відміну від інтегрального методу під час логарифмування використовується не абсолютний приріст показників, а індекси їхнього росту (зниження). Припустимо, що результативний показник можна представити у вигляді добутку трьох факторів: f = xyz. Вплив даних факторів визначається в такий спосіб:
З формул випливає, що загальний приріст результативного показника розподіляється за факторами пропорційно відношенню логарифмів факторних індексів до логарифма результативного показника. Використовуючи дані табл. 1.1, визначимо приріст товарної продукції за рахунок чисельності робітників (ЧР), кількості днів, відпрацьованих одним робітником за рік (Д) і середньоденний виробіток (ДВ) за факторною моделлю:
ТП = ЧР ´ Д ´ ДВ (1.29)
Перевага способу логарифмування полягає у відносній простоті обчислень і більш високій точності розрахунків. Сферу застосування прийомів детермінованого факторного аналізу в систематизованому вигляді можна представити наступною матрицею представленою в табл. 1.5. Таблиця 1.5 Сфера застосування прийомів детермінованого аналізу
Знання сутності даних прийомів, сфери їхнього застосування, процедури розрахунків – необхідна умова кваліфікованого проведення аналізу.
Економіко-математичні методи, використовувані в економічному аналізі Метод кореляційно-регресивного аналізу Метод кореляційно-регресивного аналізу широко використовується для визначення тісноти зв'язку між показниками, що не знаходяться у функціональній залежності. Щільність зв'язку між досліджуваними явищами вимірюється кореляційним відношенням (для криволінійної залежності). Для прямолінійної залежності обчислюється коефіцієнт кореляції. Однією з розповсюджених аналітичних задач, що розв'язуються з застосуванням кореляційно-регресивного методу, є задача на запуск – випуск. Припустимо, що існують фактичні дані про запуск і випуск промислових виробів (табл. 1.6). Таблиця 1.6 Фактичні дані запуску – випуску промислових виробів, тис. шт.
Потрібно визначити залежність випуску виробів у середньому від їхнього запуску, склавши відповідне рівняння регресії. Значення x і y визначаються за формулами:
Подальшим обчисленням надається таблична форма, що підвищує їхню наочність (табл. 1.7). Таблиця 1.7 Таблична форма обчислення
Близькість зв'язку між показниками запуску та випуску вимірюється коефіцієнтом кореляції, що обчислюється за формулою
Підставляючи відповідні значення, одержимо:
Вводячи формулу зв'язку лінійної підстановки (у = a0 + аi х), визначимо залежність випуску промислових виробів від їхнього запуску. Для цього добирається система нормальних рівнянь:
Величини Sx22 і Sxiyi представлені в наступній табл. 1.8. Таблиця 1.8 Дані для обчислення
Значення а0 визначаємо за першим рівнянням:
Підставляючи знайдене вираження а0 у друге рівняння, знаходимо значення аi:
102 (15,9 – 17 а1) + 1798а1 = 1686,3 1621,8 – 1734 а1 + 1798а1 = 1686,3 64а1 = 1686,3: 1321,8 64а1 = 64,5
а1 = 1,01
а0 = 15,9 – 17 ´ 1,01 а0 = 15,9 – 17,17 а0 = - 1,27
Отже, рівняння регресії в остаточному варіанті має такий вигляд:
У = -1,27 +1,01
Перевірка:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.206.87 (0.007 с.) |

 ;
;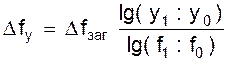 ;
;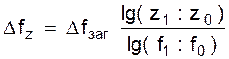 .
.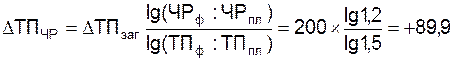 тис. грн.;
тис. грн.;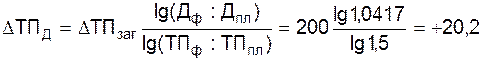 тис. грн.;
тис. грн.;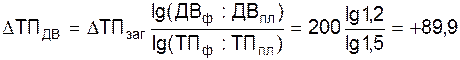 тис. грн.;
тис. грн.;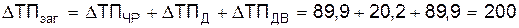 тис. грн.
тис. грн.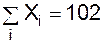
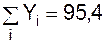
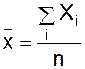 ;
; 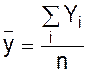 ;
; 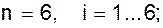



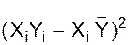




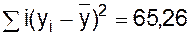
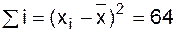
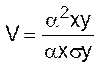 . (1.30)
. (1.30) ;
; ;
;

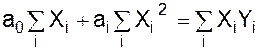 .
.

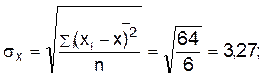
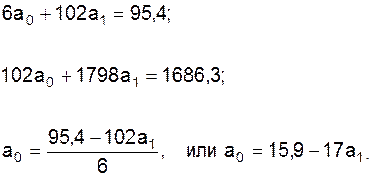
 (1.31)
(1.31)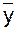 = -1,27 +1,01 ´ 17 = -1,27 + 17,17 = 15,9
= -1,27 +1,01 ´ 17 = -1,27 + 17,17 = 15,9


