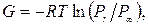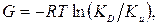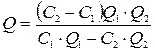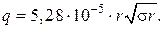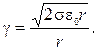Методы оценки энергетических параметров

 

Важность энергетического подхода к свойствам сыпучих формовочных материалов в настоящее время не вызывает сомнения. Активация позволяет в широких пределах изменять энергетические параметры как на поверхности, так и в объеме частиц за счет глубоких структурных преобразований, приводящих к усилению или снижению активности различных поверхностных центров, накоплению или уменьшению электростатического заряда. Следовательно, просматриваются интересные перспективы управления процессами обогащения, измельчения, активации, смешивания с целью удаления или связывания вредных примесей, плакирования наполнителей специальными добавками на уровне механохимического синтеза, получения «дезактивированных» материалов или возможность специального наведения дефектов и электрического заряда, приготовления композиций и составов с заданными свойствами.

 

Рентгеноструктурные методы

Изменение активности материалов происходит за счет изменения поверхностной и внутренней свободной энергии. Причем вклад внутренней энергии в значение общей свободной энергии вещества составляет 10–80 %.

Величину удельной поверхностной энергии оценивают количественно через твердость минералов при царапании, шлифовании, вдавливании или же по теплоте растворения (или смачивания) дисперсных порошков. Определяют ее и через работу, затрачиваемую на обработку:

A = G · S,

где G – удельная поверхностная энергия; S – удельная поверхность материала.

Величину внутренней энергии материалов оценить количественно в настоящее время пока не удается в связи с тем, что передача энергии материалу осуществляется неравномерно во времени и пространстве. Кроме того, происходит наложение поверхностных и внутренних превращений, первичных и вторичных процессов активации.

Поэтому определяют суммарную энергию, аккумулированную веществом, по изменению теплоты термической диссоциации или по изменению растворимости. Изменение свободной энергии связано с растворимостью, упругостью пара, константами равновесия, температурой и теплотой фазовых превращений, энергией ативации следующими формулами:

где R – универсальная газовая постоянная; Т – абсолютная температура; Р_r, Р_∞ – равновесная упругость пара над частицами, соответственно, с кривизной поверхности радиуса r и над плоской поверхностью; С_r, С_∞ – равновесная растворимость вещества, соответственно, с кривизной поверхности радиуса r и над плоской поверхностью; К_а, К_u – константы равновесия в системе, соответственно, для активированных и идеальных кристаллов; К_D, К_u – константы скорости реакций с жидкостью, соответственно, диспергированных и идеальных кристаллов; Т _ф.п, l – температура и скрытая теплота фазового перехода.

Степень активности материалов оценивается, как правило, исходя из целей активации, которые определяют режимы обработки. Исследуются физические и химические процессы, затем оцениваются свойства самих материалов и свойства изделий на их основе.

Возможные превращения в материалах в процессе активации зависят от условий обработки и могут задаваться в соответствии с целью активации. Для каждого типа перехода вещества в новое качество рекомендуются определенные методы оценки:

– полиморфное превращение без изменения химического состава (рентгенография);

– аморфизация кристаллической решетки без изменения химического состава (рентгенография, ИК-спектроскопия);

– ионное замещение без изменения кристаллической структуры (рентгеноструктурный или химический анализ, ИК-спектроскопия);

– изменение координационного числа без изменения химического состава (расчет разности энергетических коэффициентов);

– изменение кристаллической структуры и химического состава, связанное с растворением отдельных компонентов (химический анализ, расчет свободной энергии реакции);

– диссоциация веществ (химический анализ, расчет свободной энергии);

– разрушение кристаллической решетки минерала с растворением всех компонентов (химический анализ, расчет свободной энергии);

– разрушение кристаллической структуры и вещества на элементы (химический анализ, расчет свободной энергии).

Для различных превращений рекомендуются конкретные формулы для расчета энергетического состояния системы.

Превращения в материалах и переход их в новое качество являются результатом множества физических процессов. На каждом этапе подготовки материалов отмечаются следующие физические процессы, которые в области сверхвысоких энергий инициируют химические превращения и реакции (обмена, разложения, синтеза): эмиссия фотонов, быстрых и медленных электронов, статическая электризация и разряды, эмиссия компонентов решетки, возбуждение колебаний решетки, образование и миграция решеточных и электронных дефектов, локальные разогревы, аморфизация, внедрение примесей, пластическая деформация и массоперенос между твердыми телами.

Для исследования процессов на таком уровне используются новейшие методы: электронная микроскопия, рентгеновские методы, методы ядерного магнитного резонанса (ЯМР) и электронного парамагнитного резонанса (ЭПР), инфракрасной спектроскопии (ИК-спектроскопия), дифференциально-термический анализ, фотометрия, люминесценция и др. Наиболее широко для оценки энергетического состояния применяются методы рентгенографического, спектрального, термического анализов и электрофизические методы. Степень аморфизации решетки материалов А _м по данным рентгеноструктурного анализа определяется из соотношения

А _м = 100 – К,

где К представляет собой отношение интенсивности основных рефлексов, оцененных по высоте пика активированного материала J _изм к интенсивности пика исходного материала J _исх.

Изменение размеров кристаллитов и величины микроискажений определяют методом рентгеноструктурного анализа. Для оценки указанных эффектов применяются гармонический анализ, в основу которого положено изучение формы линий рентгенограмм, и метод аппроксимации, согласно которому эффекты определяются по интегральной полуширине основных рефлексов. Рентгенографический и спектральный анализы позволяют оценить степень структурных превращений, характер изменения химических связей и изменение химического состава материала.

Дифференциально-термический анализ позволяет определить положение и характер пиков экзо- и эндотермических эффектов, что дает возможность оценить степень структурных преобразований в активированном материале.

Рентгенографическую съемку можно осуществлять, например, на дифрактометре УРС-50 ИМ на К_a-излучении при следующих режимах: напряжение на трубке – 35кВ, ток – 10 мА, ширина щели – 0,1 мм, скорость съемки – 2 град/мин. В рентгеновских камерах Дебая диаметром 57,3 мм на установке УРС-50 хорошие дебаеграммы получают на хромовом К_a-излучении при следующих режимах: напряжение на трубке – 45 кВ, ток – 5 мА, экспозиция – 2 ч на каждый образец.

Энергетическое состояние кристаллической структуры материалов можно определять по интенсивности и ширине характерных для материала пиков на рентгенограмме, а также сравнительным анализом дебаеграмм.

 

Электрофизические методы

Изучение электрофизических свойств материалов возможно на доступной аппаратуре с использованием не очень сложных методик эксперимента. При этом различные электрофизические свойства позволяют достаточно объективно оценить энергетическое состояние частиц твердых материалов.

На базе известных физических законов, таких как закон Кулона, величина напряженности электрического поля, потенциал, а также определение удельного электросопротивления по известному электросопротивлению и его температурной зависимости исследуют силы электрического взаимодействия, напряженность и потенциал поля заряженной частицы. По изменению удельного электрического сопротивления (УЭС) с температурой рассчитывается энергия активации проводимости. Кроме того, используя специальную ячейку, можно вычислить диэлектрическую проницаемость материала и тангенс угла диэлектрических потерь.

Удельное электрическое сопротивление материалов обусловлено поверхностной и объемной проводимостью и зависит от химического состава, размера, упаковки, напряженности электрического поля частиц. Из-за адсорбции газов, примесей, влаги поверхностный слой частицы отличается по свойствам от основной массы частицы, где проводимость является электронной или ионной. При исследовании пыли в интервале 20–300 °С, например до 90–180 °С (для различных пылей), УЭС увеличивается, а затем снижается, то есть тепловое возбуждение электронов приводит к уменьшению проводимости, а предварительная ионизация порошков вызывает повышение проводимости и снижение УЭС. Объясняется это уменьшением энергии активации проводимости, то есть работы «отрыва» электрона от решетки. Механическое возбуждение приводит также к снижению УЭС.

Диэлектрик, помещенный во внешнее электрическое поле, испытывает смещение внутренних связанных зарядов. При этом возникает поляризация, выражающаяся в том, что на его поверхности появляются заряды противоположных знаков. В любом диэлектрике напряженность внутреннего поля меньше, чем в вакууме. Отношение напряженности поля в вакууме к напряженности поля в веществе и является относительной диэлектрической проницаемостью диэлектрика ε.

Как было отмечено выше, удельное электросопротивление и диэлектрическая проницаемость зависят от химической природы, размера частиц и напряженности электрического поля поляризационных зарядов на их поверхности. Мелкодисперсные диэлектрики обладают меньшим сопротивлением, а накопление статического электричества на поверхности частиц вызывает его повышение. В результате величина удельного объемного электросопротивления будет зависеть от того, какой процесс превалирует: диспергация или активация материала. Удельное объемное электросопротивление ρ, Ом, определяется из соотношения

где R_x – электросопротивление ячейки с материалом, Ом; С _В – электроемкость незаполненной ячейки, пФ.

Диэлектрическая проницаемость зависит главным образом от химической природы материалов, но с изменением дисперсности и активности материала изменяется. Оценивается диэлектрическая проницаемость e соотношением

ε = С_x / С _В,

где С_х – электроемкость ячейки с материалом, пФ.

Тангенс угла диэлектрических потерь tg δ определяет электрическую энергию, которая рассеивается в диэлектрике, обращаясь в тепло, и зависит от структуры кристаллической решетки, плотности упаковки в решетке. Более плотная упаковка ионов обусловливает малые значения tg δ. Рассчитывают tgδ по уравнению:

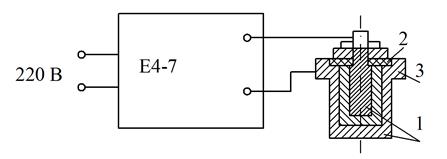
где Q ₁, Q ₂ – добротность измерительного контура без ячейки и с замеренной ячейкой соответственно.

Исследуемые материалы в виде увлажненных дистиллированной водой порошков помещаются в специальную измерительную ячейку, представляющую собой металлический сосуд из нержавеющей стали с цилиндрическими электродами. Для измерения R_x используется мост переменного тока (Р577), значение С исследуется резонансным методом с использованием измерителя добротности Е4-7 (рис. 23).

Измерение емкости С и добротности контура Q определяется на заданной частоте f. Для измерения указанных величин измерительный контур с известной индуктивностью L, которая может резонировать на указанной частоте измерения, настраивается в резонанс без подключения ячейки и определяются значения С ₁ и Q ₁. Затем подключается ячейка с емкостью С_х, и контур снова настраивается в резонанс путем подбора внутренней емкости. При этом фиксируются значения С ₂ и Q ₂. Емкость С_x рассчитывают по формуле:

 

Рис. 23. Схема установки с ячейками для измерения

диэлектрических свойств материалов: 1 – электроды; 2 – изолятор;

3 – исследуемый материал

Добротность исследуемой емкости вычисляют по формуле:

Погрешность измерения величин ρ, ε, tg δ зависит от погрешности значений R_х, C, Q и составляет менее 3,5 %.

На электросопротивление диэлектриков влияет температура. Определение температурной зависимости электросопротивления дает возможность судить о состоянии внутреннего электрического слоя материала-диэлектрика, а также о механизме электропроводимости и энергии активации зарядов (токоносителей). Схема установки приведена на рис. 24.

 

а

б

Рис. 24. Схема установки (а) и ячейки (б) для определения удельного сопротивления: 1 – токоподводы; 2 – электроды; 3 – исследуемый материал; 4 – кварцевая трубка; 5 – струбцина

 

Графическая зависимость между логарифмом удельного электросопротивления и величиной 1/ T представляет собой прямую линию, угол наклона которой к оси 1/ T определяет энергию активации зарядов (ЭАП). При увеличении температуры диэлектрика наклон прямой изменяется, возникает излом, что свидетельствует об изменении типа проводимости. Кроме этого, излом на графике может свидетельствовать о наличии фазовых переходов.

Аналитически температурная зависимость удельного электросопротивления выражается следующим образом:

где Е _А – энергия активации; k – постоянная Больцмана; Т – абсолютная температура.

Логарифмирование этого выражения дает

где А – постоянная, зависящая от природы материала.

Полученная формула есть не что иное, как уравнение первого порядка, представляющее собой прямую линию. Продифференцировав это выражение по 1/ Т, имеем

а ln r / a (1 / T) = E _A / k.

Левая часть уравнения есть тангенс угла наклона φ прямой к оси 1 / Т. Произведя замену, получим

tg φ = E _A / k.

Значит, энергия активации проводимости (ЭАП) равна:

E _A = k ∙ tg φ.

Величина ЭАП в определенном температурном интервале – это отражение кристаллического состояния диэлектрика, степени активации состояния внутреннего электрического поля.

Известно аномальное увеличение сопротивления минералов в определенном диапазоне температур, что объясняется удалением влаги, которая там присутствует. В активированных материалах, имеющих внутреннее электрическое поле за счет наличия огромного количества заряженных частиц, молекулы воды, заряжаясь зарядами противоположного знака, удерживаются силами электрического взаимодействия, которые возникают при непосредственном контакте частиц материала и молекул воды.

Слабо активированные материалы с меньшими внутренними дефектами «расстаются» с молекулами воды при более низких температурах. Для сильно активированных материалов нужно наличие более высокого «разориентирующего» действия теплового поля для нарушения упорядоченного электрического поля и удаления молекул воды. Вместе с «миграцией» молекул должно меняться давление насыщенного пара над поверхностью материала. Равновесная величина давления пара зависит от размера частиц материала и описывается уравнением Томпсона (Кельвина), которое для частиц, несущих заряд, имеет вид

где s – коэффициент поверхностного натяжения воды; r – размер частицы материала, м; q – заряд частицы, Кл; e₀ – электрическая постоянная, Ф/м; V_m – удельный объем; R – универсальная газовая пос­тоянная; T – абсолютная температура.

По графику P = f (t) можно определить температуру, соответствующую максимальному значению P ₀. Это температура, при которой почти все молекулы воды покидают материал. Кроме того, можно полагать, что при этой температуре давление пара воды над выпуклой поверхностью частицы радиуса r становится равным давлению P над плоской поверхностью, поскольку число ионов воды настолько мало, что не станет сказываться влияние кривизны частиц.

Таким образом, граничное условие, при котором ионы воды будут удерживаться электрическими силами, представляет собой равенство P = P ₀. Тогда можно записать

Логарифмирование этого выражения по основанию ехр дает

Поскольку величина V_m / RT ≠ 0, принимаем

Решая это уравнение относительно q, получаем

Представляя численные значения ε₀ = 8,85∙10^–12 Ф/м и π = 3,14, находим

Поверхностное натяжение воды s берется из таблиц для температуры, когда происходит дегидратация поверхности. Температура выбирается из зависимости Р = f (Т).

Данный метод позволяет по величине размера частиц активированных веществ и значению коэффициента поверхности натяжения воды при температуре, соответствующей максимальному значению Р, количественно оценить величину заряда частиц.

Для характеристики зарядов частиц разных размеров наиболее удобной является величина плотности заряда γ, то есть γ = q / S, где S – площадь поверхности тела сферической формы. Таким образом,

Значение Р можно рассчитать по упрощенной формуле Томсона:

P = P ₀ + V ₀ / (V _п – V _ж) s ∙ 2 / r,

где Р, Р ₀ – давление пара над выпуклой и плоской поверхностями; V _ж, V _п – удельный объем воды и пара; s – коэффициент поверхностного натяжения воды при данной Т (выбирается из зависимости P = f (Т); r – радиус кривизны частицы.

Напряженность электрического поля Е, В/м, создаваемого зарядом одной частицы, определяется по формуле

Е = q / (8πe₀ r ²).

Потенциал φ этого поля равен

φ = q / (4πε₀ r).

Зная заряд частиц, нетрудно определить величину электрической силы взаимодействия, когда электрически заряженные частицы находятся в непосредственном контакте. Значение электрической силы F_Е, действующей на единицу поверхности заряженной частицы, определяется в системе СИ по формуле

F_Е = q ² / (2ε₀ S ²),

где S – величина поверхности заряженной частицы.

При значении электрических зарядов частиц, имеющих порядок 10^–12–10^–13 Кл, значение поверхностной силы составляет 10²–10³ Н/м².

Расчет кулоновских сил взаимодействия заряженных частиц, то есть сил, обусловленных предварительным зарядом частиц, проводится по формуле

F_k = q ² / (4ε₀ d ⁴),

где d – зазор между заряженными частицами, который принимается равным диаметру частицы.