Поиск равновесия в смешанных стратегиях

 

Многим читателям вполне достаточно понять суть смешанных стратегий на качественном концептуальном уровне и затем возложить задачу вычисления фактических показателей на компьютерную программу, способную рассчитать смешанные стратегии, когда у каждого игрока есть любое число чистых стратегий (при этом некоторые из них могут даже не использоваться в равновесии)[155]. Эти читатели могут пропустить оставшуюся часть главы без ущерба для понимания изложенного материала. Но тем читателям, которые знают алгебру и геометрию хотя бы на уровне курса средней школы, мы предлагаем более подробную информацию по этой теме[156].

Сначала рассмотрим алгебраический метод. Число стратегий «слева» в смешанной стратегии игрока, выполняющего пенальти, – это неизвестное, которое нужно найти; назовем его х. Поскольку это относительная доля, число стратегий «справа» составит (1 – х). Показатель эффективности такой смешанной стратегии в случае, если вратарь выберет стратегию «слева», составит 58 x + 93(1 – x) = 93–35 x процентов, а если он выберет стратегию «справа» – 95 x + 70(1 – x) = 70 + 25 x процентов. Эти два показателя будут равными, если 93–35 x = 70 + 25 x, или 23 = 60 x, или x = 23∕60 ≈ 0,383.

Мы можем также найти решение графическим методом, отобразив результаты различных вариантов смешивания стратегий на графике. Доля ударов слева в смешанной стратегии бьющего игрока, которую мы обозначили как х, отображается на горизонтальной оси от 0 до 1. По каждому варианту смешивания стратегий одна из двух линий отображает показатель эффективности стратегии бьющего игрока в случае, если вратарь выберет чистую стратегию «слева» (обозначенную на графике буквой Л), а другая – показатель эффективности стратегии бьющего игрока, если он выберет чистую стратегию «справа» (буква П). Первая линия начинается в точке, соответствующей значению 93 (значение выражения 93–35 x при х = 0), и опускается до значения 58 (значение этого же выражения при х = 1). Вторая линия начинается в точке, соответствующей значению 70 (значение выражения 70 + 25 x при х = 0), и повышается до значения 95 (значение этого же выражения при х = 1).

 

 

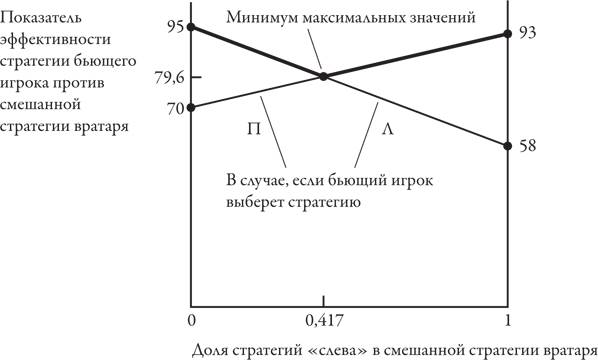
Вратарю необходимо удерживать показатель эффективности стратегии бьющего игрока на как можно более низком уровне. Следовательно, если бы структура смешанной стратегии бьющего игрока была известна вратарю, он выбрал бы стратегию «слева» или «справа», отображенную одним из тех сегментов двух линий, которые расположены ниже точки пересечения. Эти сегменты, выделенные жирным и образующие перевернутую букву V, отображают минимальный показатель эффективности стратегии игрока, выполняющего штрафной удар, если вратарь использует выбор бьющего игрока с наибольшей выгодой для себя. Бьющему игроку необходимо выбрать из этих минимальных значений максимальный показатель эффективности своей смешанной стратегии. Это значение соответствует вершине перевернутой буквы V, то есть точке пересечения двух линий. Внимательно изучив график, получим те же координаты этой точки, которые дает алгебраическое решение: x = 0,383, а показатель эффективности стратегии – 79,6 процента.

Точно так же можно проанализировать смешанную стратегию вратаря. Обозначим число стратегий «слева» в смешанной стратегии вратаря как y. Тогда (1 – y) – это доля стратегий «справа» в его смешанной стратегии. Если бьющий игрок выберет стратегию «слева» против этой смешанной стратегии, средний показатель эффективности его стратегии составит 58 y + 95(1 – y) = 95–37 y, а если стратегию «справа» – 93 y + 70(1 – y) = 70 + 23 y. Эти два показателя будут равными, если 95–37 y = 70 + 23 y, или 25 = 60 y, или y = 25∕60 ≈ 0,417.

Графический анализ смешанной стратегии вратаря представляет собой простую модификацию такого же анализа стратегии игрока, выполняющего пенальти. Для этого построим график, отображающий результаты различных вариантов смешивания стратегий вратаря. Доля позиций «слева» в смешанной стратегии вратаря, которую мы обозначили как y, отображается на горизонтальной оси от 0 до 1. Одна из двух линий отображает показатель эффективности стратегии вратаря в случае, если бьющий игрок выберет чистую стратегию «слева», а другая – тот же показатель, если это будет чистая стратегия «справа». По каждому варианту смешивания стратегий, который выберет вратарь, бьющий игрок должен выбрать тот вариант стратегии «слева» или «справа», который обеспечивает более высокий показатель эффективности. Этот максимум находится в вершине буквы V, образованной теми сегментами двух линий, которые выделены жирным. Вратарь должен удерживать показатель эффективности стратегии бьющего игрока на максимально низком уровне. Он может сделать это, выбрав стратегию, соответствующую нижней точке буквы V, то есть минимум максимальных значений. Этой точке соответствуют координаты y = 0,417, а показатель эффективности стратегии – 79,6 процента.

 

 

Равенство максимума минимальных значений (максимина) бьющего игрока и минимума максимальных значений (минимакса) вратаря – это и есть теорема фон Неймана – Моргенштерна о минимаксе в действии. Возможно, было бы правильнее назвать ее теоремой о равенстве максимина и минимакса, но общепринятое название короче и легче запоминается.