Задача для тренировки мышления № 3

Предположим, компания Rainbow’s End нашла поставщика более дешевых рубашек, поэтому ее цена снизилась с 20 до 11,6 доллара, тогда как в B. B. Lean осталась прежняя цена – 20 долларов. Сделайте перерасчет таблицы выигрышей и найдите новое равновесие Нэша.

 

У ценовой игры есть много других аспектов, но они более сложны, чем тот материал, который мы рассматривали до настоящего момента. Поэтому проанализируем эти аспекты далее в данной главе. В заключение текущего раздела сделаем несколько общих комментариев по поводу равновесия Нэша.

Есть ли равновесие Нэша в каждой игре? Ответ: в большинстве случаев да, при условии, что мы обобщим концепцию действий или стратегий, разрешив смешивание ходов. Именно это условие было указано в знаменитой теореме Нэша. Мы рассмотрим концепцию смешивания ходов более подробно в следующей главе. Игры, в которых нет равновесия Нэша даже в случае смешивания ходов, настолько сложны или трудны для понимания, что их углубленное изучение под силу только специалистам по теории игр.

Можно ли считать равновесие Нэша эффективным решением в играх с параллельными ходами? Некоторые аргументы и доказательства по этому вопросу изложены в данной главе далее, и наш ответ будет сдержанно-утвердительным.

Есть ли в каждой игре единственное равновесие Нэша? Нет. Рассмотрим ряд важных примеров игр с несколькими равновесиями Нэша, а также проанализируем новые вопросы, возникающие в связи с этим.

 

Какое равновесие выбрать?

 

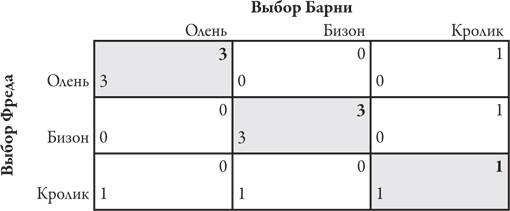
Давайте попробуем применить теорию Нэша к игре в охоту. Найти оптимальные ответные ходы в этой игре достаточно легко. Фреду следует просто сделать тот же выбор, который, по его мнению, сделает Барни. Вот каким будет результат:

 

 

Следовательно, в этой игре есть три равновесия Нэша[116]. Какое из них выберут в итоге оба игрока? Или они вообще не смогут достичь равновесия в этой игре? Концепция равновесия Нэша сама по себе не дает ответов на эти вопросы. Для этого необходим дополнительный анализ, основанный на других рассуждениях.

Если бы Фред и Барни встретились на холостяцкой вечернике[117], которую устроил их общий друг, выбор охоты на оленя оставил бы более заметный след в их памяти. Если бы согласно обычаям их общины глава семьи говорил, отправляясь на охоту: «Пока, сынок»[118], – более очевидным для них был бы выбор охоты на бизона. Но если бы в семье было принято говорить на прощание: «Береги себя», – более значимым был бы безопасный выбор, гарантирующий хотя бы какое-то количество мяса независимо от выбора другого охотника, а именно охота на кролика.

А что именно представляет собой эта «значимость»? Одна стратегия, скажем, охота на оленя, может быть значимой для Фреда, но этого недостаточно для того, чтобы он выбрал именно ее. Он должен спросить себя, является ли эта стратегия столь же значимой для Барни. А это, в свою очередь, поднимет вопрос о том, считает ли Барни эту стратегию значимой для Фреда. Выбор одного из нескольких равновесий Нэша требует решения той же задачи с размышлениями о размышлениях, что и сама концепция равновесия Нэша.

Для того чтобы такая «значимость» позволяла решить эту задачу, она должна включать в себя несколько уровней. Успешный выбор одного из равновесий Нэша в ситуации, когда оба игрока размышляют и действуют изолированно друг от друга, сводится к такой цепочке рассуждений: для Фреда должно быть очевидным, что для Барни очевидно, что для Фреда очевидно… что это правильный выбор. Если равновесие подразумевает выбор, очевидный до бесконечности в данном смысле, иными словами, если на нем сходятся ожидания игроков, мы называем это фокальной точкой. Это одна из нескольких новаторских концепций, которые ввел в теорию игр Томас Шеллинг.

Существование такой фокальной точки в игре зависит от многих условий, самое важное из которых – общий опыт игроков, который может быть историческим, культурным, лингвистическим или совершенно случайным. Вот несколько примеров, иллюстрирующих эту идею.

Начнем с одного из классических примеров Шеллинга. Предположим, вам сказали, что вы должны встретиться с кем-то в Нью-Йорке в назначенный день, но не сказали, где и когда. Вы даже не знаете, с кем именно вы должны встретиться, поэтому не можете связаться с этим человеком заранее (но вам сказали, что вы узнаете друг друга, когда встретитесь). Вам сказали также, что другой человек получил те же инструкции.

На первый взгляд ваши шансы на успех могут показаться довольно низкими: Нью-Йорк – огромный город, да и день длится долго. Но на самом деле многие люди успешно решают эту задачу. Со временем встречи все просто: полдень – это очевидная фокальная точка; ожидания сходятся на ней почти инстинктивно. С местом встречи немного сложнее, но в Нью-Йорке не так много ориентиров, на которых могут сойтись ожидания игроков. Это существенно сужает диапазон выбора и повышает вероятность успешной встречи.

Томас Шеллинг провел эксперименты с участием людей, приехавших из Бостона и Нью-Хейвена. В те времена эти люди должны были отправиться в Нью-Йорк поездом и приехать на Центральный вокзал; для них фокальной точкой были бы часы на этом вокзале. В наши дни многие люди выбрали бы в качестве места встречи Эмпайр-Стейт-билдинг – возможно, из-за фильма Sleepless in Seattle («Неспящие в Сиэтле») или An Affair to Remember («Незабываемый роман»). Для других очевидным «перекрестком миров» стала бы площадь Таймс-сквер.

Один из нас (Барри Нейлбафф) провел этот эксперимент в рамках ТВ-шоу Primetime на канале АВС, в программе под названием Life: The Game («Жизнь – игра»)[119]. Шесть пар совершенно незнакомых людей отвезли в разные районы Нью-Йорка и попросили найти другие пары, не имея никакой информации, за исключением того, что другая пара будет искать их на тех же условиях. Обсуждение плана действий проходило в каждой паре в полном соответствии с логикой Шеллинга. Каждая пара анализировала, каким может быть очевидное место встречи, а также что думают по этому поводу участники другой пары. Одна команда (скажем, команда А) пришла в своих рассуждениях к выводу о том, что другая команда (команда Б) тоже в это же время размышляла о том, что очевидно для команды А. В итоге три пары прибыли к Эмпайр-Стейт-билдинг и еще три пары – на Таймс-сквер. Все пары выбрали полдень в качестве времени встречи. Но им предстояло разобраться еще с некоторыми вопросами: в Эмпайр-Стейт-билдинг две смотровые площадки на разных уровнях, а Таймс-сквер – очень большая площадь. Однако участники эксперимента проявили находчивость (в том числе использовали таблички с надписями), благодаря чему всем шести парам удалось найти друг друга[120].

Для успешного решения такой задачи важно не то, что место очевидно для вас или для других игроков, а то, что для каждого из вас очевидно, что для других очевидно, что… И если Эмпайр-Стейт-билдинг соответствует этому критерию, значит каждая команда должна отправиться именно туда, даже если кому-то не совсем удобно туда добираться, поскольку это единственное место, в котором каждая команда может рассчитывать найти другую. Если бы в игре участвовали только две команды, одна из них могла бы подумать, что очевидная фокальная точка – это Эмпайр-Стейт-билдинг, а другая – что Таймс-сквер столь же очевидное место встречи; в таком случае эти две команды не смогли бы встретиться.

Профессор Дэвид Крепс из Стэнфордской школы бизнеса провел на занятиях следующий эксперимент. Каждый из двух студентов должен был сделать выбор, не имея возможности обменяться информацией с другим студентом. Их задача состояла в том, чтобы разделить между собой список городов. Одному студенту достался Бостон, другому – Сан-Франциско (эта информация была открытой, так что оба знали города друг друга). Затем каждому дали список из девяти американских городов (Атланта, Чикаго, Даллас, Денвер, Хьюстон, Лос-Анджелес, Нью-Йорк, Филадельфия и Сиэтл) и предложили выбрать несколько из этих городов. Если студенты получали в результате два непересекающихся подмножества городов, каждому из них давали приз. Но если в их общем списке не хватало одного города или были повторения, они оба ничего не получали.

Сколько равновесий Нэша существует в этой игре? Если студент, за которым закреплен Бостон, выберет, скажем, Атланту и Чикаго, а студент, которому достался Сан-Франциско, – остальные города (Даллас, Денвер, Хьюстон, Лос-Анджелес, Нью-Йорк, Филадельфию и Сиэтл), это и есть равновесие Нэша: учитывая выбор одного игрока, любое изменение выбора, сделанного другим игроком, приведет либо к пропуску, либо к совпадению городов в их списках и снизит выигрыш того, кто отклонился от равновесия. Такая же аргументация применима в случае, если один студент выберет Даллас, Лос-Анджелес и Сиэтл, а другой – шесть оставшихся городов. Иными словами, в данной игре существует столько равновесий Нэша, сколько существует способов разделить список из девяти чисел на два разных подмножества. Существует 29 = 512 таких способов; следовательно, в данной игре присутствует огромное число равновесий Нэша.

Могут ли у участников этой игры сойтись ожидания, которые создадут фокальную точку? Если оба игрока были американцами или жили в США уже достаточно долго, в 80 процентах случаев они делили список по географическому принципу: студенты, за которыми был закреплен Бостон, выбирали города, расположенные к востоку от Миссисипи, а студенты, за которыми был закреплен Сан-Франциско, – к западу[121]. Такая координация была гораздо менее вероятной, если один или оба студента не являлись гражданами США. Следовательно, национальность или культура могут способствовать созданию фокальной точки. Когда в ходе эксперимента Крепса у пар студентов не было общего опыта, порой они выбирали города по алфавиту, но даже в этом случае отсутствовала очевидная точка раздела. Если бы общее число городов в списке было четным, фокальной точкой могло бы стать разделение списка поровну, но с девятью городами сделать это невозможно. Таким образом, нельзя утверждать, что игроки всегда найдут способ выбрать одно из множества равновесий Нэша благодаря сходимости своих ожиданий; вполне возможно, что им не удастся найти фокальную точку[122].

Далее предположим, что каждому из двух игроков предложили выбрать натуральное число. Если оба игрока выбирают одно и то же число, каждый из них получает приз. Если оба выбирают разные числа, они не получают ничего. В подавляющем большинстве случаев выбор выпадает на число 1: это первое число ряда целых (натуральных) чисел; это наименьшее число и так далее; следовательно, оно и есть фокальной точкой. В данном случае причины, по которым это число выделяется среди других чисел, носят сугубо математический характер.

Томас Шеллинг приводит в качестве иллюстрации пример, когда двое или больше людей приходят вместе в людное место и теряют друг друга. Куда должен пойти каждый из них, чтобы встретиться с остальными? Если бы в таком месте, скажем в универмаге или на железнодорожном вокзале, было специальное окошко под названием «Потерявшиеся» или «Найденные», оно вполне могло бы стать фокальной точкой. В данном случае причины того, что мост заметен, носят лингвистический характер. Иногда места встречи создаются специально для того, чтобы обеспечить сходимость ожиданий. Например, в Германии и Швейцарии на многих вокзалах выделены места с хорошо заметными указателями Treffpunkt («Место встречи»).

В игре во встречу замечательно не только то, что в ней два игрока находят друг друга, но и то, что фокальная точка играет большую роль во многих других случаях стратегического взаимодействия. Один из самых важных примеров такого взаимодействия – Фондовый рынок. Джон Мейнард Кейнс – пожалуй, самый известный экономист ХХ столетия – объяснял поведение фондового рынка, проводя аналогию с популярным в те времена газетным конкурсом. Во время такого конкурса в газете печаталось несколько фотографий лиц, а читатели должны были угадать, какое именно лицо посчитает самым красивым большинство участников голосования[123]. В этой ситуации логика рассуждений сводится к следующему: о каком лице большинство людей подумают, что большинство других людей подумают, что большинство других подумают… что оно самое красивое. Если бы лицо одного из участников конкурса было существенно красивее всех остальных, оно и стало бы необходимой фокальной точкой. Но задача читателей редко бывала столь простой. Представьте себе, что есть сотня финалистов конкурса, которых почти невозможно отличить друг от друга, разве что по цвету волос. Из сотни финалистов только у одного рыжие волосы. Вы выбрали бы рыжеволосого?

Следовательно, задача состоит не в том, чтобы составить однозначное мнение о красоте, а в том, чтобы найти фокальную точку этих размышлений. Как же достичь согласия в этом? Читатели должны найти такое согласие, не имея возможности общаться друг с другом. Можно рассуждать по принципу «выбрать самого красивого человека», но сделать это гораздо труднее, чем выбрать рыжеволосого человека, или человека с симпатичной щелью между передними зубами (как у Лорен Хаттон), или человека с родинкой (как у Синди Кроуфорд). Все, что отличает человека от других, становится фокальной точкой и обеспечивает сходимость ожиданий. Именно поэтому не стоит удивляться, что многие из лучших моделей мира не обладают совершенной внешностью; они скорее почти идеальны, но у них есть какой-либо милый изъян, который придает их внешнему виду индивидуальность и привлекает к себе всеобщее внимание, а значит, играет роль фокальной точки.

Кейнс использовал конкурсы красоты как метафору для фондового рынка, где каждый инвестор стремится купить акции, которые вырастут в цене, а значит, акции, курс которых повысится, по мнению широкого круга инвесторов. «Горячие» акции – это акции, по поводу которых все думают, что все думают… что это «горячие» акции. Тот факт, что акции разных компаний пользуются повышенным спросом в разное время, объясняется разными причинами, такими как хорошо разрекламированное первичное размещение акций, рекомендация известного аналитика и так далее. Концепция фокальной точки позволяет объяснить, почему такое большое внимание привлекают к себе круглые числа, например 10 000 в случае индекса Доу-Джонса или 2500 в случае индекса NASDAQ. Эти индексы рассчитываются на основании стоимости акций, входящих в состав соответствующего портфеля. Число 10 000 не имеет никакого внутреннего значения; оно служит в качестве фокальной точки только потому, что ожидания чаще сходятся на круглых числах.

Смысл всего сказанного состоит в том, что равновесие вполне может быть выбрано под влиянием порыва. Не существует фундаментального закона, который гарантировал бы, что будет выбрана самая красивая участница конкурса красоты или что лучшие акции будут расти в цене быстрее всех. Есть только факторы, которые способствуют этому. Высокая прогнозируемая прибыль на акцию – это то же самое, что внешность участницы конкурса красоты: одно из множества необходимых, но ни в коем случае не достаточных условий, требуемых для того, чтобы обуздать не поддающиеся контролю порывы и предпочтения.

Многим специалистам по теории математических игр не нравится зависимость исхода игры от исторических, культурных или лингвистических факторов или от условных инструментов, таких как круглые числа. Они предпочли бы, чтобы решение зависело только от абстрактных математических фактов об игре, таких как число игроков, стратегии, имеющиеся в распоряжении каждого из них, а также выигрыш каждого игрока в зависимости от стратегии, выбранной другими игроками. Мы не согласны с этой точкой зрения. Мы считаем закономерным тот факт, что исход игры, в которую играют люди, взаимодействующие друг с другом в обществе, зависит от социальных и психологических аспектов этой игры.

Возьмем в качестве примера ведение переговоров по поводу заключения той или иной сделки. В этом случае интересы игроков совершенно несовместимы: б о льшая доля для одного означает меньшую долю для другого. Однако во многих случаях, если сторонам не удается договориться, обе не получают ничего и могут понести серьезные убытки – например, когда срываются переговоры по поводу заработной платы, после чего начинается забастовка или наступает локаут (временная остановка работы по инициативе работодателя). Интересы обеих сторон таких переговоров совпадают в том смысле, что обе стремятся избежать подобных разногласий. Они могут сделать это, если найдут фокальную точку, а также если каждая сторона считает, что другая больше ничего не уступит. Именно поэтому так часто встречается вариант разделения 50:50. Это простой и понятный вариант, у которого есть одно важное преимущество: он кажется справедливым. Кроме того, при наличии таких соображений этот вариант обеспечивает сходимость ожиданий.

Рассмотрим в качестве примера проблему чрезмерно высокой оплаты труда генеральных директоров компаний – CEO. Во многих случаях СЕО действительно заботятся о своей репутации. Получит ли такой человек 5 или 10 миллионов долларов, на самом деле не окажет большого влияния на его жизнь. (Нам легко так говорить, поскольку для нас обе цифры не более чем абстракция.) Какое же «место встречи» интересует большинство СЕО? Быть исключительным. Каждый стремится оказаться в верхней половине лучших. Все СЕО хотят «встретиться» именно там. Проблема в том, что это «место встречи» может вместить в себя только половину желающих. Но они обходят эту проблему благодаря повышению заработной платы. Каждая компания платит своему СЕО больше средней заработной платы топ-менеджеров за предыдущий год, чтобы все думали, будто у них исключительный генеральный директор. В итоге происходит необоснованное повышение заработной платы СЕО до чрезвычайно высокого уровня. Для того чтобы решить эту проблему, необходимо найти другую фокальную точку. Например, в прошлом СЕО компаний заслуживали серьезную репутацию благодаря бескорыстному служению обществу. Соперничать в этом направлении – хорошая мысль во всех отношениях. Текущая фокальная точка в плане оплаты труда топ-менеджеров сформировалась под влиянием опросов Business Week и консультантов по вопросам бизнеса. Изменить эту ситуацию будет нелегко.

Вопрос справедливости – это также вопрос выбора фокальной точки. В Декларации целей развития на пороге тысячелетия, а также в книге Джеффри Сакса The End of Poverty[124]говорится о том, что, если выделить на развитие всего один процент ВВП, можно к 2025 году покончить с нищетой. Главное здесь то, что фокальная точка вклада в развитие выражена в процентах от доходов, а не в абсолютном значении. Это означает, что богатые страны должны сделать более весомый вклад, чем бедные. Очевидная справедливость этого принципа может обеспечить сходимость ожиданий в данном вопросе. Но будут ли обещанные средства действительно выделены, остается только гадать.