Неожиданные последствия изменений в смешанных стратегиях

 

Даже в играх с нулевой суммой равенство смешанных стратегий обладает на первый взгляд необычными свойствами. Вернемся к примеру с футбольным пенальти и предположим, что вратарь усовершенствует навыки отражения штрафных ударов, сделанных с естественной для него стороны (справа), что снизит показатель эффективности бьющего игрока с 70 до 60 процентов. Как это скажется на вероятности смешивания стратегий вратаря в разных пропорциях? Ответ на этот вопрос можно получить, сместив соответствующую линию на графике. Число позиций «слева» в равновесной смешанной стратегии вратаря увеличится с 41,7 до 50 процентов. Это означает, что, если вратарь усовершенствует навыки отражения штрафных ударов справа, он будет реже использовать эту сторону!

Хотя на первый взгляд это кажется странным, причина вполне понятна. Когда вратарь улучшает свою способность отбивать пенальти справа, бьющий игрок начнет реже делать удары справа от вратаря. В ответ на увеличение числа ударов слева вратарь увеличит долю стратегий «слева» в своей смешанной стратегии. Смысл укрепления слабых навыков в том, что вам не придется пользоваться ими так часто.

 

 

Вы можете проверить истинность этого утверждения, рассчитав долю ударов слева и справа в смешанной стратегии бьющего игрока после такого изменения навыков вратаря. Вы увидите, что доля ударов слева увеличится с 38,3 до 47,1 процента.

Работа вратаря над усилением навыка отражения ударов справа действительно принесет свои плоды: средний процент забитых мячей при равновесной смешанной стратегии снизится с 79,6 до 79,5.

Если хорошо подумать, этот кажущийся парадокс подчиняется обычной логике теории игр. То, что лучше всего для вас, зависит не только от вас самих, но и от действий других игроков. Именно к этому и сводится суть стратегической взаимозависимости.

 

 

Учебный пример: Джанкен на Ступеньках [157]

 

Действие происходит в суши-баре в деловой части Токио. Такаши и Уити сидят у стойки бара и пьют саке в ожидании своих заказов. Каждый из них заказал фирменное блюдо суши-бара – уни сашими (икра морского ежа). К сожалению, шеф-повар сообщает им, что у него осталась только одна порция этого блюда. Кто из двух молодых людей уступит другому?

В Америке эти двое могли бы подбросить монету. В Японии они скорее сыграют в игру джанкен, на Западе более известную как «камень, ножницы, бумага». Разумеется, к этому моменту вы уже стали настоящими экспертами по этой игре, поэтому для того, чтобы несколько усложнить задачу, мы используем здесь один из ее вариантов, который называется «джанкен на ступеньках».

В этот вариант джанкена играют на ступеньках. Как и обычно, игроки одновременно выбрасывают знаки камня, ножниц и бумаги. Но теперь победитель очередного раунда поднимается вверх по лестнице: на пять ступенек, если он сыграл «бумагой» (раскрытая ладонь с пятью пальцами), на две ступеньки – в случае «ножниц» (два пальца) и на одну ступеньку – если выбросил «камень» (пальцы сложены в кулак). В случае ничьей игра повторяется. Как правило, победителем становится тот, кто находится на верхней ступеньке лестницы. Мы немного упростим игру, приняв предположение, что цель каждого игрока – как можно больше опередить соперника.

Каким будет равновесное сочетание стратегий в этой версии игры джанкен?

 

Анализ примера

 

Поскольку с каждой очередной ступенькой победитель продвигается вперед, а проигравший отстает, это игра с нулевой суммой. Проанализировав все возможные пары ходов, получим матрицу игры. Выигрыши в этой таблице измеряются числом ступенек.

 

 

Как найти равновесное сочетание выбрасывания «бумаги», «ножниц» и «камня»? Мы уже рассказали о таких простых методах, как числовые расчеты и построение графика, которые применимы, когда у каждой стороны только одна альтернатива: удар справа и удар слева. Но в игре джанкен на ступеньках – три варианта выбора.

Прежде всего необходимо выяснить, какие стратегии войдут в состав равновесной смешанной стратегии. В данном случае важны все три варианта. Для того чтобы убедиться в этом, представьте себе, что Уити никогда не будет выбрасывать камень. В таком случае Такаши не станет играть бумагой; тогда Уити не будет выбрасывать ножницы. Если продолжить эту цепочку рассуждений, получится, что Такаши не будет использовать камень при условии, что Уити не использует бумагу. Если Уити никогда не будет выбрасывать камень, это сведет на нет все его стратегии, а значит, такое предположение было бы ложным. Аналогичные доводы подтверждают тот факт, что оставшиеся две стратегии тоже необходимо включить в смешанную стратегию Уити (и Такаши).

Теперь мы знаем, что в равновесной смешанной стратегии должны присутствовать все три стратегии. Остается выяснить, когда именно они будут использоваться. Игроки заинтересованы в получении максимального выигрыша, а не в смешивании стратегий ради самого смешивания. Уити готов использовать камень, ножницы и бумагу методом случайного выбора только при условии, что все три стратегии в равной степени привлекательны. (Если бы камень обеспечивал Уити более высокий выигрыш, чем ножницы или бумага, то ему следовало бы играть только камнем, но такая стратегия не была бы равновесной.) Таким образом, особый случай, когда все три стратегии обеспечивают Уити один и тот же ожидаемый выигрыш, определяет структуру равновесной смешанной стратегии Такаши.

Предположим, Такаши использует следующий принцип смешивания:

 

p = вероятность того, что Такаши выбросит бумагу;

q = вероятность того, что Такаши выбросит ножницы;

1 – (p + q) = вероятность того, что Такаши выбросит камень.

 

В таком случае, если Уити сыграет камнем, он будет отставать на пять ступенек, если Такаши сыграет бумагой (р), и выиграет одну ступеньку, если Такаши сыграет ножницами (q), а чистый выигрыш составит –5 p + q. Точно так же Уити получит следующий выигрыш за счет каждой из своих стратегий:

 

Камень: –5 p + 1 q + 0(1 – (p + q)) = –5 p + q.

Ножницы: 2 p + 0 q – 1(1 – (p + q)) = 3 p + q – 1.

Бумага: 0 p – 2 q + 5(1 – (p + q)) = –5 p – 7 q + 5.

 

Эти три варианта могут быть в равной степени привлекательными для Уити только при выполнении следующего условия:

 

– 5 p + q = 3 p + q – 1 = –5 p – 7 q + 5.

 

Решив эти уравнения, получим: p = 1∕8, q = 5∕8 и (1 – p – q) = 2∕8.

Это определяет структуру равновесной смешанной стратегии Такаши. Поскольку эта игра симметрична, Уити будет использовать свои стратегии по методу случайного выбора с такой же вероятностью.

Обратите внимание на то, что, если и Уити, и Такаши используют свое равновесное сочетание стратегий, их ожидаемый выигрыш за счет каждой стратегии будет равен нулю. К такому исходу игры приводят не все смешанные стратегии, однако в симметричных играх с нулевой суммой возможен только такой результат. Нет причин, почему Уити должен находиться в более выгодном положении, чем Такаши, и наоборот.

В главе 14 рассматривается еще один учебный пример, посвященный теме выбора и случая, – «Как обмануть всех: игровые автоматы Лас-Вегаса».

 

Глава 6

Стратегические ходы

 

Изменение хода игры

 

Миллионы людей каждый год дают новогодние обещания. Поиск в Google по ключевым словам «новогодние обещания» дает множество ссылок. По данным сайта правительства США, самое популярное новогоднее обещание – «сбросить вес». За ним следуют: «выплатить долг», «накопить денег», «найти более подходящую работу», «привести себя в хорошую физическую форму», «правильно питаться», «получить хорошее образование», «пить меньше алкоголя» и «бросить курить»[158].

В англоязычной версии Википедии новогоднее обещание определяется как «обязательство в отношении того или иного проекта или привычки, которое в большинстве случаев влечет за собой изменение жизни к лучшему». Обратите внимание на слово «обязательство». Большинство людей имеют сугубо интуитивное представление об этой концепции, понимая ее как намерение, обещание или клятву. Позже мы дадим точное определение обязательства в контексте теории игр.

Что же происходит со всеми этими замечательными планами улучшения жизни? Согласно результатам опроса, проведенного CNN, 30 процентов новогодних обещаний не дотягивают даже до февраля и только одно из пяти – выполняется на протяжении полугода или более[159]. Тому есть много причин: люди ставят перед собой слишком большие цели; у них нет эффективных методов оценки достигнутых успехов; не хватает времени и так далее. Однако гораздо более важная причина неудачи состоит в том, что, подобно Оскару Уайльду, большинство людей способны противостоять чему угодно, кроме соблазна. Когда они видят и чувствуют запах всех этих бифштексов, картошки фри и десертов, их диета обречена на провал. Когда вас притягивают к себе новые электронные гаджеты, ваше твердое намерение держать свою кредитную карточку в кошельке ослабевает. Когда кто-то сидит в удобном кресле и смотрит спортивные передачи по ТВ, реальные физические упражнения кажутся ему намного более трудной работой.

Многие консультанты по медицинским вопросам и по образу жизни дают рекомендации, как достичь успеха в выполнении новогодних обещаний. К числу таких рекомендаций относятся базовые принципы: ставить достижимые и измеримые цели; упорно трудиться, постепенно приближаясь к их достижению; установить режим здорового питания и физических тренировок и вносить в этот процесс разнообразие, чтобы избежать скуки; не отчаиваться; не сдаваться после любых неудач. Среди этих рекомендаций есть и стратегии создания правильных стимулов, важный элемент которых – система поддержки. Людям советуют присоединяться к группам, участники которых вместе придерживаются диет или занимаются физическими упражнениями, а также рассказывать о своих обещаниях членам семьи и друзьям. Безусловно, ощущение того, что вы не одиноки в своем стремлении, очень помогает добиться успеха, но то же самое касается и позорной перспективы публичного провала.

Один из нас (Барри Нейлбафф) успешно использовал фактор стыда в программе Life: The Game («Жизнь – игра») в рамках ТВ-шоу Primetime на канале АВС[160]. Как мы рассказали во вступительной главе, участники шоу с избыточным весом согласились сфотографироваться в бикини с условием, что фотографии тех, кому не удастся сбросить семь килограммов за два месяца, будут показаны по национальному телевидению и размещены на веб-сайте программы. Стремление избежать этого стало для участников шоу мощным стимулом. В итоге все, кроме одного, сбросили минимум по семь килограммов; одному участнику не удалось достичь такого результата, но его отставание было совсем небольшим.

Какое отношение ко всему этому имеет теория игр? Борьба с лишним весом (или стремление накопить больше денег) – это игра сегодняшнего «я» человека (которое мыслит в долгосрочной перспективе и стремится улучшить жизнь или повысить благосостояние) против будущего «я», которое мыслит в краткосрочной перспективе (и которому свойственна склонность переедать и тратить слишком много денег). Обещание сегодняшнего «я» представляет собой обязательство вести себя правильно. Но это обязательство должно быть непреложным: будущее «я» необходимо лишить возможности отказаться от него. Сегодняшнее «я» может добиться этого, предприняв какое-либо сопутствующее действие: например, можно сфотографироваться в слишком открытом наряде и разрешить режиссеру программы показать фотографии по ТВ, если не удастся сбросить требуемое количество килограммов. Это меняет игру посредством изменения стимулов будущего «я». Соблазн переедать или тратить слишком много денег никуда не исчез, но ему противостоит перспектива позорного разоблачения.

Действия, которые меняют игру таким образом, чтобы обеспечить более благоприятный результат для игрока, совершающего эти действия, называются стратегическими ходами. В этой главе мы подробно объясним и проиллюстрируем многие из таких ходов. При этом нам предстоит проанализировать два аспекта: что необходимо сделать и как это сделать. Первую задачу можно решить с помощью науки под названием «теория игр», тогда как вторая характеризуется своей спецификой в каждой конкретной ситуации, а продумать эффективные стратегические ходы во всех возможных ситуациях – это скорее искусство, чем наука. Мы изложим основные принципы этой науки и попытаемся обучить вас элементам искусства на конкретных примерах. Однако дальнейшее совершенствование искусства ведения тех игр, в которые вы играете, зависит от вас самих и от ваших знаний о сложившейся ситуации.

А теперь позвольте нам привести второй пример изменения хода игры. Представьте себе, что вы юноша, живущий в небольшом американском городке в 1950-х годах. Погожий субботний день. Вы с друзьями играете в игру, которая определит лидера. Сегодняшнее состязание начинается с игры в труса. Ваши автомобили мчатся навстречу друг другу, и вы знаете: тот, кто свернет первым, – это и есть проигравший, или трус. Но вы хотите победить.

Это опасная игра. Если оба ее участника будут добиваться победы, в лучшем случае они окажутся в больнице. Мы анализировали игру в труса в главе 4 в контексте равновесия Нэша (на примере охотников каменного века Фреда и Барни) и пришли к выводу, что в этой игре два равновесия Нэша: одно – когда вы едете прямо, а ваш соперник сворачивает в сторону, а другое – когда вы сворачиваете в сторону, а ваш соперник едет прямо. Безусловно, вы предпочитаете первый вариант второму. Теперь поднимем анализ этой игры на более высокий уровень. Можете ли вы сделать что-то, чтобы добиться более предпочтительного для вас исхода игры?

Один из способов – создать себе репутацию человека, который никогда не сворачивает в сторону. Для того чтобы сделать это, необходимо не раз победить в таких играх в прошлом, то есть вопрос можно поставить так: что вы могли бы сделать в тех играх?

А вот еще один замысловатый, но эффективный способ. Представьте себе, что вы сняли руль с вала и выбросили его в окно так, чтобы это видел ваш соперник. Теперь он знает, что вы просто не можете свернуть в сторону. Вся ответственность за предотвращение столкновения ложится на него. Вы изменили ход игры. В новой игре у вас только одна стратегия – ехать прямо. В таком случае единственный оптимальный (на самом деле лучший из худших) ответный ход вашего соперника состоит в том, чтобы свернуть. Вы беспомощны как водитель, но именно эта беспомощность сделает вас победителем игры в труса.

Этот способ изменения хода игры кажется неожиданным только на первый взгляд. Выбросив руль, вы ограничили свою свободу действий. Разве может принести выгоду сокращение числа возможных вариантов выбора? В этой игре возможность свернуть в сторону – не более чем возможность стать трусом, а значит, в данном случае свобода выбирать – это свобода проиграть. Из нашего анализа стратегических ходов можно извлечь и другие неожиданные уроки.

Кроме того, этот пример содержит серьезное предостережение по поводу стратегических ходов. Их успех не гарантирован, а порой они могут быть явно опасными. В реальной жизни между действием и наблюдением существует определенная временная задержка. В случае игры в труса представьте себе, что будет, если такая же мысль придет в голову и вашему сопернику и вы оба увидите рули друг друга летящими в воздухе? Слишком поздно. Вы беспомощно мчитесь к неизбежному столкновению.

Так что можете применять эти методы на свой страх и риск, но не предъявляйте к нам претензий, если вас постигнет неудача.

 

Немного истории

 

Отдельные люди и целые народы еще в далеком прошлом брали на себя обязательства, высказывали угрозы и давали обещания. Они интуитивно понимали важность достоверности таких действий, использовали стратегии и изобретали контрстратегии против действий других игроков. Когда гомеровский Одиссей привязал себя к мачте, он взял на себя твердое обязательство не поддаться пению сирен. Родители понимают, что хладнокровная угроза наказать ребенка за плохое поведение звучит не очень убедительно, а вот угроза «Ты хочешь, чтобы мама рассердилась?» куда более правдоподобна. На протяжении всей истории короли отлично понимали, что добровольный обмен заложниками (когда отдавали любимого ребенка или кого-то из родственников в семью противника) позволяет сделать их взаимные обещания о мирном сосуществовании более достоверными.

Теория игр помогает осмыслить и унифицировать концептуальную схему таких стратегий. Однако в первое десятилетие своего существования теория игр была сфокусирована на описании различных типов равновесий в той или иной конкретной игре: метода обратных рассуждений в играх с последовательными ходами, минимакса в играх с нулевой суммой с участием двух игроков и равновесия Нэша в более общей категории игр с параллельными ходами. Все эти стратегии иллюстрировались в контексте таких важных игр, как дилемма заключенных, игра в доверие, семейный спор и игра в труса[161]. Томас Шеллинг первым развил идею о том, что один или оба игрока могут предпринять действия, направленные на изменение хода игры, – именно эта идея стала центральной темой всей теории игр. В статьях Томаса Шеллинга, опубликованных в 1950–1960-х годах и собранных впоследствии в книгах The Strategy of Conflict (1960) и Arms and Influence (1965)[162], содержится точное описание таких концепций, как обязательство, угроза и обещание. Шеллинг четко определил, что именно необходимо для того, чтобы стратегия была достоверной. Кроме того, он проанализировал такую тонкую и рискованную стратегию, как балансирование на грани, которую раньше толковали совершенно неправильно.

Более точное формальное определение концепции достоверности стратегии, а именно концепции совершенного равновесия субигры, которая представляет собой обобщение метода обратных рассуждений, о котором шла речь в главе 2, сформулировал несколько лет спустя Райнхард Зелтен, который в 1994 году стал одним из первых специалистов по теории игр (наряду с Джоном Нэшем и Джоном Харсаньи), получивших Нобелевскую премию.

 

Обязательства

 

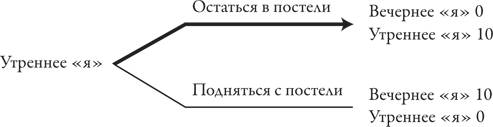
Разумеется, не обязательно ждать Нового года для того, чтобы пообещать себе что-то хорошее. Вы каждый вечер можете принимать решение, что проснетесь рано, чтобы начать день с зарядки или утренней пробежки. Но при этом вы прекрасно знаете, что, когда наступит утро, захотите полежать в постели еще полчаса (а может, и больше). Это игра между вашим решительно настроенным вечерним «я» и будущим слабовольным утренним «я». И в этой игре утреннее «я» имеет преимущество второго хода. Однако вечернее «я» может изменить ход игры, включив будильник, для того чтобы воспользоваться преимуществом первого хода. Это своего рода обязательство подняться с постели, когда зазвонит будильник, но сработает ли такой метод? (Заметим, что еще более ранняя версия вашего «я» могла бы найти и купить будильник, у которого нет кнопки отключения, но вряд ли такое возможно.) И все же вечернее «я» сделает это обязательство достоверным, если поставит будильник на шкаф у противоположной стены комнаты, а не на ночной тумбочке: в таком случае утреннему «я» придется встать с постели, чтобы выключить звонок будильника. Если и этого недостаточно и утреннее «я», спотыкаясь, возвращается в постель, пусть одновременно со звонком будильника включается и начинает варить кофе ваша кофеварка, чтобы заманчивый запах вытащил ваше утреннее «я» из постели[163].

Этот пример прекрасно иллюстрирует два аспекта обязательств и их достоверности: что и как. «Что» – это научный аспект, или аспект теории игр: использовать преимущество первого хода. «Как» – практический аспект, или искусство: придумать способы, которые помогут вам предпринять достоверные стратегические ходы в той или иной ситуации.

Техническую или научную сторону обязательства вставать по звонку будильника можно проиллюстрировать с помощью древовидных диаграмм, о которых шла речь в главе 2. В исходном варианте игры, в котором вечернее «я» не предпринимает никаких действий, дерево игры выглядит очень просто:

 

 

Утреннее «я» остается в постели и получает свой максимальный выигрыш (которому мы присвоили 10 баллов), оставив вечернему «я» минимальный выигрыш (который мы установили в размере 0 баллов). Конкретное число баллов здесь не имеет особого значения – важно только то, что для каждого варианта «я» приоритетному варианту присваивается больше баллов, чем менее приоритетному.

Вечернее «я» может изменить ход игры следующим образом:

 

 

Теперь размер выигрыша имеет значение и требует дополнительных объяснений. Верхняя основная ветка дерева, отображающая ситуацию, когда вечернее «я» не включает будильник, выглядит так же, как и предыдущее дерево. В нижней основной ветке мы предположили, что вечернее «я» понесет небольшие затраты, если включит будильник (мы оценили эти затраты в 2 балла). Следовательно, если утреннее «я» отреагирует на звонок будильника и поднимется с постели, вечернее «я» получит 8 баллов вместо 10 в исходном варианте игры. Но если утреннее «я» проигнорирует звонок будильника, вечернее «я» получит –2 балла, поскольку затраты на включение будильника оказались напрасными. Утреннее «я» понесет затраты в связи с тем раздражением, которое оно испытает, услышав звонок будильника; эти затраты составят всего 1 балл, если утреннее «я» быстро поднимется и выключит будильник, и целых 15 баллов, если оно останется в кровати, а будильник будет продолжать звенеть, превратив удовольствие от пребывания в постели (10 баллов) в убыток –5 баллов (= 10–15). Если будильник включен, утреннее «я» выберет –1 балл вместо –5 баллов и поднимется с постели. Вечернее «я» предусмотрит эту возможность и решит, что включение будильника даст ему в итоге 8 баллов, что лучше 0, которые оно получило бы в исходной игре[164]. Следовательно, равновесная стратегия, полученная методом обратных рассуждений, выглядела бы так: утреннее «я» поднимается с постели, если будильник включен, а вечернее «я» включает будильник.

Более неожиданный аспект обязательства можно увидеть, представив эту игру в виде таблицы, а не в виде дерева игры.

 

 

В таблице показано, что по каждой конкретной стратегии утреннего «я» выигрыш вечернего «я» от включения будильника меньше, чем в случае, если будильник не будет включен: –2 меньше 0, а 8 меньше 10. Следовательно, для вечернего «я» стратегия «будильник включен» доминируемая по отношению к стратегии «будильник выключен». Тем не менее вечернее «я» предпочитает взять на себя обязательство и включить будильник!

Разве возможна хоть какая-то польза от выбора доминируемой стратегии и отказа от доминирующей? Для того чтобы ответить на этот вопрос, необходимо более глубоко проанализировать концепцию доминирования. Стратегия «будильник выключен» доминирующая по отношению к стратегии «будильник включен» с точки зрения вечернего «я», поскольку по каждой конкретной стратегии утреннего «я» стратегия «будильник выключен» обеспечивает вечернему «я» более крупный выигрыш, чем стратегия «будильник включен». Если утреннее «я» выберет стратегию «остаться в постели», вечернее «я» получит 0 баллов при выключенном будильнике и –2 балла при включенном будильнике; если утреннее «я» выберет стратегию «подняться с постели», вечернее «я» получит 10 баллов при выключенном будильнике и 8 баллов при включенном будильнике. Если ходы в игре делаются одновременно или если вечернее «я» делает свой ход вторым, оно не сможет повлиять на выбор утреннего «я» и ему придется принять этот выбор как должное. Но ведь цель стратегического хода состоит именно в том, чтобы изменить выбор другого игрока, а не воспринимать его как должное. Если вечернее «я» выберет стратегию «будильник включен», утреннее «я» решит подняться с постели и вечернее «я» получит выигрыш 8 баллов; если вечернее «я» выберет стратегию «будильник выключен», утреннее «я» решит остаться в постели и вечернее «я» получит выигрыш 0 баллов – а 8 баллов больше, чем 0. В таком случае выигрыши 10 и –2 балла даже не стоит анализировать и сравнивать с выигрышами 8 и 0 баллов соответственно. Следовательно, в игре с последовательными ходами концепция доминирования утрачивает свою значимость для игрока, делающего первый ход.

Из примеров, приведенных в этой главе, вы поймете, о чем идет речь, без построения таких деревьев или таблиц, поэтому в большинстве случаев будем описывать соответствующие рассуждения только с помощью слов. Но при желании вы можете углубить понимание самой игры и метода дерева игры, построив деревья игры для соответствующих примеров.

 

Угрозы и обещания

 

Обязательство – это безусловный стратегический ход (как говорится в рекламе Nike, «просто сделай это»), который другие игроки вынуждены принять как должное. Вечернее «я» просто включает будильник, ставит его на комод и выставляет таймер на кофеварке. Вечернее «я» больше не может ничего предпринять; можно даже сказать, что к утру оно прекращает свое существование. Утреннее «я» – это ведомый игрок, поскольку оно делает свой ход вторым. Подняться с постели – его оптимальный (или лучший из худших) ответный ход на взятое вечерним «я» обязательство.

С другой стороны, угрозы и обещания – более сложные условные ходы, которые требуют, чтобы вы заранее установили правило ответной реакции, определяющее ваши действия в ответ на ход другого игрока в реальной игре. Угроза – это правило ответной реакции, которое подразумевает наказание других игроков за то, что их действия не отвечают вашим ожиданиям.

Правило ответной реакции предписывает, как вы отреагируете на ходы других игроков. Даже если в реальной игре вы выступаете в качестве игрока, делающего второй ход, правило ответной реакции должно быть введено до того, как другие игроки сделают свои ходы. Если мама говорит ребенку: «Никакого десерта, пока не съешь шпинат», – тем самым она устанавливает такое правило ответной реакции. Разумеется, это правило необходимо ввести и четко объяснить ребенку еще до того, как он отдаст свой шпинат собаке.

Из этого следует, что такие ходы потребуют от вас более сложных методов изменения хода игры. В деле введения правила ответной реакции и доведения этого правила до сведения других игроков необходимо присвоить себе статус игрока, делающего первый ход. Вы должны обеспечить достоверность этого правила, иными словами – заставить других игроков поверить в то, что, если и когда наступит время предпринять заявленные ответные действия, вы непременно сделаете это. Возможно, для этого вам понадобится несколько изменить ход игры, чтобы вы смогли убедиться в правильности такого выбора в соответствующей ситуации. Но на следующем этапе игры вы снова должны стать игроком, делающим второй ход, с тем чтобы у вас появилась возможность отреагировать на выбор другого игрока. Для этого вам может понадобиться изменить порядок ходов в игре, а это создает дополнительные трудности с реализацией стратегического хода.

Для того чтобы проиллюстрировать эти идеи, воспользуемся примером с ценовой войной между компаниями посылочной торговли B. B. Lean и Rainbow’s End, о которых шла речь в главах 3 и 4 в контексте игр с параллельными ходами. Эти компании конкурируют друг с другом на рынке сбыта конкретного продукта – рубашек из высококачественной ткани шамбре. Давайте вспомним основные моменты этой ситуации. Обе компании заинтересованы в том, чтобы договориться и назначить на этот продукт монопольную цену – 80 долларов за одну рубашку. В таком случае каждая получит прибыль в размере 72 тысячи долларов. Однако для каждой компании существует соблазн назначить меньшую цену, чем у конкурента, и если они обе сделают это, то согласно равновесию Нэша, каждая назначит на свой продукт цену всего 40 долларов и заработает только 40 тысяч долларов прибыли. Это их дилемма заключенных, или игра, в которой проиграют все: если каждая компания поддастся соблазну заработать больше прибыли для себя, в убытке окажутся обе.

Теперь посмотрим, могут ли стратегические ходы решить эту дилемму. Обязательства одной из компаний не снижать цену недостаточно: другая просто использует это с выгодой для себя в ущерб первой компании. А как насчет условных ходов? Компания Rainbow’s End могла бы прибегнуть к угрозе («Если вы назначите низкую цену, мы тоже сделаем это») или к обещанию («Если вы сохраните цену на монопольном уровне, мы тоже сделаем это»). Но если в реальной игре с выбором цен для публикации в каталоге ходы делаются одновременно в том смысле, что ни одна компания не увидит каталог конкурента до того, как отдаст свой каталог в печать, как компания Rainbow’s End вообще сможет отреагировать на ход B. B. Lean? Ей придется изменить ход игры, с тем чтобы получить возможность выбирать цену уже после того, как станет известна цена другой компании.

В таком случае чаще всего используется оговорка о продаже продукции по цене не выше, чем у конкурентов. Компания Rainbow’s End печатает в своем каталоге цену 80 долларов, но с таким примечанием: «Мы продадим этот товар по любой более низкой цене, назначенной любым конкурентом». При таком подходе каталоги печатаются и рассылаются одновременно, но если в B. B. Lean пошли на обман и напечатали в своем каталоге цену меньше 80 долларов, вплоть до цены равновесия Нэша – 40 долларов, тогда Rainbow’s End автоматически снизит свою цену до такого же уровня. Покупателю, который отдает предпочтение или лоялен по отношению к Rainbow’s End, нет необходимости переходить к B. B. Lean: он может просто заказать нужный ему продукт у Rainbow’s End, как и всегда, и заплатить за него ту цену, которая указана в каталоге B. B. Lean.

Мы еще вернемся к этому примеру для того, чтобы проиллюстрировать другие аспекты стратегических ходов. А пока просто запомните, что у данной ситуации есть два разных аспекта: научный аспект, или «что» (угроза адекватно отреагировать на снижение цены), и аспект искусства, или «как» (оговорка о продаже продукции по цене не выше, чем у конкурента, которая делает угрозу осуществимой и достоверной).

 

Сдерживание и принуждение

 

Угрозы и обещания имеют ту же задачу, что обязательства: заставить других игроков сделать то, чего они не сделали бы в противном случае. В случае угроз и обещаний целесообразно разбить их общую задачу на две категории. Если вы хотите помешать другим игрокам сделать то, что они сделали бы в противном случае, речь идет о сдерживании. Противоположный вариант – заставить других игроков сделать то, чего они в противном случае не сделали бы, – можно назвать принуждением[165].

Если грабитель банка держит в заложниках сотрудников, заявляя при этом, что убьет их, если его требования не будут выполнены, он высказывает принуждающую угрозу. Когда во время холодной войны Соединенные Штаты Америки угрожали применить ядерное оружие в случае, если Советский Союз нападет на любую из стран НАТО, это была сдерживающая угроза. Этим двум типам угроз свойственна одна общая черта: обе стороны понесут дополнительные расходы, если угрозу придется привести в действие. Грабитель банка получит более строгое наказание, если его поймают и к ограблению банка добавится еще и убийство; США понесут ужасные потери в ядерной войне, тогда как можно было бы постараться наладить контакты с Европой, оказавшейся под властью Советского Союза.

Обещания тоже бывают принуждающими или сдерживающими. Принуждающее обещание направлено на то, чтобы добиться от кого-то благоприятных для вас действий. Например, обвинитель, которому нужен свидетель, для того чтобы укрепить свои позиции на суде, обещает одному из обвиняемых более мягкий приговор, если тот согласится свидетельствовать против других обвиняемых по тому же делу. Принуждающее обещание ставит целью помешать кому-то совершить действия, противоречащие вашим интересам, – как в случае, когда преступники обещают своему сообщнику защитить его, если он будет молчать. Как и два типа угроз, два типа обещаний имеют общую черту. После того как другой игрок согласился пойти навстречу пожеланиям того, кто дал ему обещание, давшему обещание игроку нет нужды отдавать обещанную награду, поэтому у него появляется соблазн нарушить обещание. Следовательно, после того как главари банды будут оправданы за отсутствием доказательств, они все равно могут убить своего сообщника во избежание будущих проблем или шантажа.