Смешивание стратегий в неантагонистических играх

 

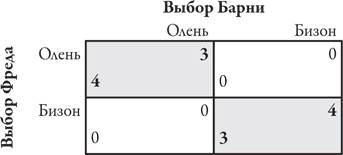
До сих пор мы рассматривали в этой главе только антагонистические игры, в которых интересы игроков полностью противоположны: игры с нулевой суммой или игры с постоянной суммой. Однако мы неизменно подчеркиваем, что в реальной жизни интересы людей могут совпадать, а могут и противоречить друг другу. Играет ли смешивание стратегий значимую роль в играх с ненулевой суммой? Да, но с некоторыми условиями.

В качестве иллюстрации еще раз рассмотрим охотничью версию игры «семейный спор», о которой шла речь в главе 4. Вспомните наших отважных охотников Фреда и Барни, которые решают (каждый в своей пещере), на какого зверя им охотиться – на оленя или на бизона. Удачная охота требует совместных усилий обоих охотников, поэтому, если они выберут противоположные варианты, никто из них не добудет мяса. И Фред, и Барни заинтересованы в том, чтобы предотвратить такой итог. Однако помимо двух вариантов благополучного исхода (при условии, что они охотятся на одном участке) нужно учесть, что Фред отдает предпочтение мясу оленя и оценивает результат совместной охоты на этого зверя как четыре вместо трех единиц мяса, тогда как у Барни противоположные предпочтения. Следовательно, таблица их выигрышей выглядит так:

 

 

Как мы уже убедились, в этой игре есть два равновесия Нэша; в таблице они выделены серым цветом. Теперь мы назвали бы их равновесиями в чистых стратегиях. Но возможно ли такое равновесие в игре со смешанной стратегией?

По каким причинам Фред выбрал бы смешанную стратегию? Возможно, он не уверен в том, что именно выберет Барни. Если под влиянием этих субъективных сомнений Фред оценивает число случаев, когда Барни выберет охоту на оленя и на бизона, как y и (1 – у) соответственно, тогда он рассчитывает на выигрыш в размере 4 y + 0(1 – y) = 4 y, если он сам выберет охоту на оленя, и 0 y + 3(1 – y), если он сам выберет охоту на бизона. Если y имеет значение, при котором 4 y = 3(1 – y), или 3 = 7 y, или y = 3∕7, тогда Фред получит один и тот же выигрыш, выбрав стратегию охоты на оленя или на бизона, а также если он решит использовать обе стратегии в любой пропорции. Предположим, что Фред смешивает стратегию охоты на оленя и на бизона в таких пропорциях, что для Барни не имеет значения, какую из чистых стратегий выбрать. (Эта игра симметрична, поэтому вы можете предположить – и подтвердить это предположение расчетами, – что Фред должен смешивать свои стратегии, выбирая охоту на оленя в x = 4∕7 случая.) При этом Барни тоже мог бы смешивать свои стратегии по такому принципу, чтобы Фреду было все равно, какую стратегию выбрать, а значит, Барни сам мог бы выбрать оптимальную стратегию. Эти два варианта смешивания стратегий – x = 4∕7 и y = 3∕7 – образуют равновесие Нэша в смешанных стратегиях.

Всегда ли такое равновесие обеспечивает удовлетворительный результат? Нет. Проблема в том, что два охотника делают свой выбор независимо друг от друга. Следовательно, Фред выберет охоту на оленя, тогда как Барни выберет охоту на бизона, в 4∕7 × 4∕7 = 16∕49 случаях, и наоборот – в 3∕7 × 3∕7 = 9∕49 случаях. Таким образом, в 25∕49 или немногим более половины случаев два охотника окажутся на разных участках и получат нулевой выигрыш. Воспользовавшись приведенными формулами, мы увидим, что каждый из них получит выигрыш в размере 4 × 3∕7 + 0 × 4∕7 = 12∕7 ≈ 1,71, что меньше выигрыша 3 в случае неблагоприятного равновесия в чистых стратегиях.

Для того чтобы избежать таких ошибок, Фреду и Барни необходимо согласовать свои действия в плане смешивания стратегий. Могут ли они сделать это, находясь в отдаленных пещерах и не имея никаких средств связи? Возможно, охотники могли бы заранее договориться о согласовании действий, опираясь на то, в каких условиях оба будут собираться на охоту. Предположим, в их местности половину дней в году по утрам идет дождь. Фред и Барни могут договориться, что оба отправятся охотиться на оленя, если в тот день пойдет дождь, и на бизона – если будет сухо. В таком случае каждый из них получит средний выигрыш в размере ½ × 3 + ½ × 4 = 3,5. Таким образом, скоординированная рандомизация обеспечивает охотникам изящный способ найти нечто среднее между благоприятным и неблагоприятным равновесием Нэша в чистых стратегиях, иными словами, воспользоваться таким инструментом, как переговоры.

Нескоординированное равновесие Нэша в смешанных стратегиях не только обеспечивает игрокам низкий выигрыш, но и является хрупким и нестабильным. Если оценка Фредом вероятности того, что Барни выберет охоту на оленя, хотя бы немного превысит значение 3∕7 ≈ 0,42857 и составит, скажем, 0,43, тогда выигрыш Фреда от выбора охоты на оленя, а именно 4 × 0,43 + 0 × 0,57 ≈ 1,72, превысит выигрыш от выбора охоты на бизона – 0 × 0,43 + 3 × 0,57 ≈ 1,71. Следовательно, Фреду нет смысла смешивать стратегии, а лучше выбрать чистую стратегию охоты на оленя. В таком случае лучший ответный ход Барни – чистая стратегия охоты на оленя, а это значит, что равновесие в смешанных стратегиях нарушено.

В заключение хотелось бы обратить ваше внимание на то, что у равновесия в смешанных стратегиях есть необычное свойство, не совсем понятное интуитивно. Предположим, выигрыш Барни изменится с 3 и 4 на 6 и 7 единиц соответственно, а выигрыш Фреда останется неизменным. Как это повлияет на пропорции смешивания стратегий? Снова обозначим символом y относительное число случаев, когда Барни, по мнению Фреда, должен выбрать охоту на оленя. В данной ситуации Фред все равно получит выигрыш в размере 4 y от выбора чистой стратегии охоты на оленя и 3(1 – y) – от выбора чистой стратегии охоты на бизона. В итоге при значении y = 3∕7 для Фреда не будет иметь значения, какую стратегию выбрать, и он будет готов к смешиванию стратегий. С другой стороны, присвоив значение х относительному числу случаев выбора охоты на оленя в смешанной стратегии Фреда, Барни получит выигрыш 6 x + 0(1 – x) = 6 x за счет чистой стратегии охоты на оленя и 0 x + 7(1 – x) = 7(1 – x) за счет чистой стратегии охоты на бизона. Приравняв эти два выражения, получим x = 7∕13. Таким образом, изменение выигрыша Барни никак не скажется на равновесии в его смешанной стратегии, но изменит пропорции в смешанной стратегии Фреда!

Поразмышляв еще немного, вы поймете, что это не так уж и странно. Возможно, Барни готов смешивать свои стратегии только потому, что он не уверен в действиях Фреда. Следовательно, в приведенных расчетах учтен выигрыш Барни и вероятность выбора, который сделает Фред. Если мы приравняем два итоговых выражения и решим полученное уравнение, то увидим, что вероятность того, какую именно пропорцию смешивания стратегий выберет Фред, зависит от выигрыша Барни, и наоборот.

Однако это настолько тонкие и на первый взгляд непривычные рассуждения, что во время проведения экспериментов большинство игроков не могут понять этого даже тогда, когда им предлагают рандомизировать выбор стратегий. Они меняют вероятность смешивания стратегий, когда меняется их собственный выигрыш, а не выигрыш другого игрока.