
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа газа при изопроцессахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Внутренняя энергия тела может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ подвергается сжатию в цилиндре под поршнем, то внешние силы совершают над газом некоторую положительную работу A'. В то же время силы давления, действующие со стороны газа на поршень, совершают работу A = – A'. Если объем газа изменился на малую величину Δ V, то газ совершает работу pS Δ x = p Δ V, где p – давление газа, S – площадь поршня, Δ x – его перемещение. При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна. В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой:
или в пределе при Δ Vi → 0:
В изохорном процессе (V = const) газ работы не совершает, A = 0. В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением:
В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, Δ U = 0. Первый закон термодинамики для изотермического процесса выражается соотношением Q = A. Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам. Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими. Работа газа в адиабатическом процессе выражается через температуры T 1 и T 2 начального и конечного состояний:
М
Молярная и удельная теплоемкость газа. Молярная теплоемкость Молярная теплоемкость — теплоемкость 1 моля идеального газа.
Теплоемкость идеального газа в изопроцессах Адиабатический В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть
Изотермический В изотермическом процессе постоянна температура, то есть Изохорный В изохорическом процессе постоянен объем, то есть
А для идеального газа
Таким образом,
где i — число степеней свободы частиц газа. Изобарный В изобарном процессе (
CP=δQ/νΔT=CV+R=((i+2)/2)*R Уде́льная теплоёмкость (Удельная теплота нагревания на один градус, обозначается как c) вещества определяется как количество тепловой энергии, необходимой для повышениятемпературы одного килограмма вещества на один градус. Единицей СИ для удельной теплоёмкости является Джоуль на килограмм - Кельвин. Следовательно, удельную теплоёмкость можно рассматривать как теплоёмкость единицы массывещества. На значение удельной теплоёмкости влияет температура вещества. К примеру, измерение удельной теплоёмкости воды даст разные результаты при 20 °C и 60 °C. Формула расчёта удельной теплоёмкости: Связь Cv и Cp: т. е. молярная теплоемкость газа при постоянном объеме СV равна изменению внутренней энергии одного моль газа при повышении его температуры на 1 К. Поскольку Um=(i /2)RT, то
Если газ нагревается при постоянном давлении, то выражение (3) можно представить в виде
Учитывая, что (Um/dT) не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется лишь температурой Т) и всегда равна СV (см. (4)), и дифференцируя уравнение Клапейрона — Менделеева pVm=RT (42.4) по T (p=const), получаем
Выражение (6) называется уравнением Майера; оно говорит о том, что Сp всегда больше СV ровно на величину молярной газовой постоянной. Это объясняется тем, чтобы осуществить нагревание газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Использовав (5), формулу (6) можно записать в виде
При исследовании термодинамических процессов важно знать характерное для каждого газа отношение Сp к СV:
Из формул (5) и (7) следует, что молярные теплоемкости зависят лишь от числа степеней свободы и не зависят от температуры. Это утверждение молекулярно-кинетической теории справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней свободы, которое проявляется в теплоемкости, зависит от температуры. Молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы. По закону равномерного распределения энергии по степеням свободы, для комнатных температур СV = (7/2)R. Из качественной экспериментальной зависимости молярной теплоемкости СV водорода (рис. 1) следует, что СV следующим образом зависит от температуры: при низкой температуре (≈50 К) СV = (3/2)R, при комнатной — CV = (5/2)R (вместо расчетных (7/2)R) и при очень высокой — СV= (7/2)R. Это можно объяснить, сделав предположение, что при низких температурах наблюдается только поступательное движение молекул, при комнатных — добавляется их вращение, а при высоких — к данным двум видам движения добавляются еще колебания молекул.
II начало термодинамики Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами. Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не должна равняться 0. Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения. Существуют несколько эквивалентных формулировок второго начала термодинамики: § Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» [1] (такой процесс называется процессом Клаузиуса). § Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона). Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло Q 1 у нагревателя, отдав Q 2 холодильнику и совершив при этом работу A = Q 1− Q 2. После этого воспользуемся процессом Клаузиуса и вернем тепло Q 2 от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже неверен.
С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса. Таким образом, постулаты Клаузиуса и Томсона эквивалентны. Другая формулировка второго начала термодинамики основывается на понятии энтропии: § «Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии). Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано. Второе начало термодинамики в аксиоматической формулировке Рудольфа Юлиуса Клаузиуса (R. J. Clausius, 1865) имеет следующий вид[2]: Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния S = S (T, x, N), называемая энтропией, такая, что ее полный дифференциал dS = δ Q / T. В состоянии с максимальной энтропией макроскопические необратимые процессы (а процесс передачи тепла всегда является необратимым из-за постулата Клаузиуса) невозможны. Ограничения С точки зрения статистической физики второе начало термодинамики имеет статистический характер: оно справедливо для наиболее вероятного поведения системы. Существованиефлуктуаций препятствует точному его выполнению, однако вероятность сколь-нибудь значительного нарушения крайне мала.
|
|||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 4252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.14.62 (0.013 с.) |


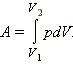
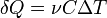

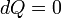 . При изменении объема температура и давление меняются, то есть
. При изменении объема температура и давление меняются, то есть 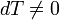 . Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: Садиаб=0.
. Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: Садиаб=0. . При изменении объема газу передается (или отбирается) некоторое количество тепла. Следовательно, теплоемкость идеального газа стремится к бесконечности:
. При изменении объема газу передается (или отбирается) некоторое количество тепла. Следовательно, теплоемкость идеального газа стремится к бесконечности: 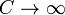
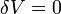 . Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение (δ A = δ VP). Первое Начало Термодинамики для изохорического процесса имеет вид:
. Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение (δ A = δ VP). Первое Начало Термодинамики для изохорического процесса имеет вид: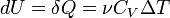
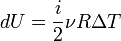
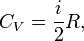
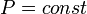 ):
):
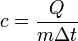 , где
, где  — удельная теплоёмкость,
— удельная теплоёмкость,  — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении),
— количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении), 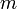 — масса нагреваемого (охлаждающегося) вещества,
— масса нагреваемого (охлаждающегося) вещества, 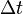 — разность конечной и начальной температур вещества.
— разность конечной и начальной температур вещества.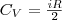 (5)
(5)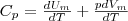
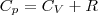 (6)
(6)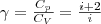 (8)
(8)


