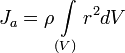Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь потенциальной энергии и силыСодержание книги
Поиск на нашем сайте
Пространство, в котором действуют консервативные силы, называется потенциальным полем.
Проекции вектора силы на оси координат:
Вектор силы можно записать через проекции:
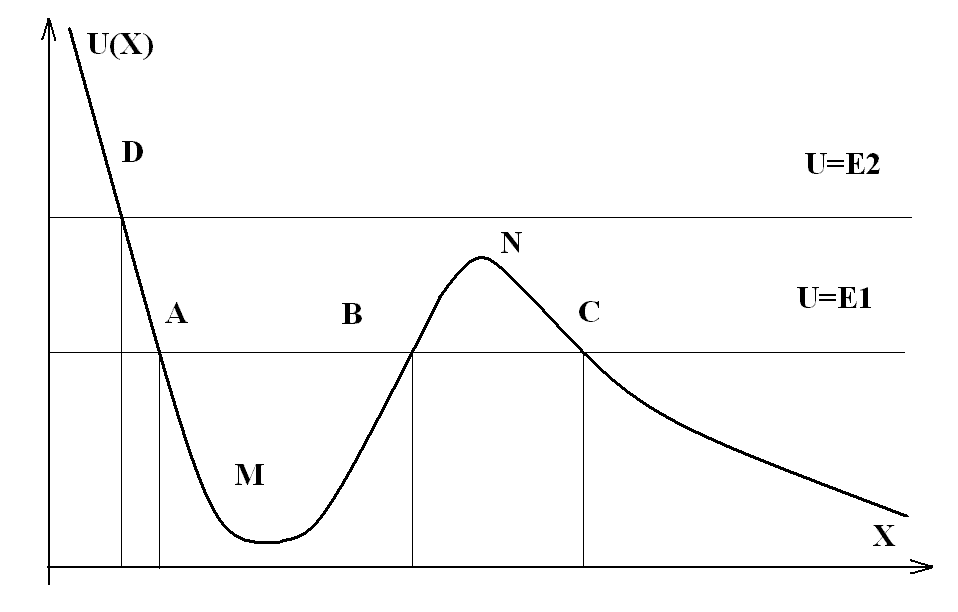
где Градиент – это вектор, показывающий направление наибыстрейшего изменения функции. Следовательно, вектор Потенциальные кривые и энергетические уровни Самый простой пример это вода в стакане.
Энергетический уровень — собственные значения энергии квантовых систем, то есть систем, состоящих из микрочастиц (электронов, протонов и других элементарных частиц) и подчиняющихся законам квантовой механики. Каждый уровень характеризуется определённым состоянием системы, или подмножеством таковых в случае вырождения. Понятие применимо к атомам (электронные уровни), молекулам (различные уровни, соответствующие колебаниям и вращениям), атомным ядрам (внутриядерные энергетические уровни) и т.д.
Импульс (II закон Ньютона с использованием импульса). И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости:
Связь: Если коротко, то F = dp/dt т.е. скорость изменения импулься тела равна действующей силе. Эта формула -- непосредственное следствие определения импулься p = m*v и второго закона Ньютона F = m*a. Действительно, дифференцируя обе части определения импульса p = m*v, имеем: dp/dt = m*dv/dt = m*a = F.
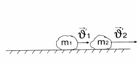
Закон сохранения импульса Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная суммаимпульсов всех тел (или частиц) замкнутой системы есть величина постоянная.
Вращательное движение Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна. При равномерном вращении (T оборотов в секунду), Частота вращения — число оборотов тела в единицу времени.
Период вращения — время одного полного оборота. Период вращения T и его частота ν связаны соотношением T = 1 / ν.
При вращательном движении все точки тела движутся по окружностям, центры которых лежат на прямой. Эту прямую называют осью вращения (прямая 00' на рис.9). Окружности лежат в парал-лельных плоскостях, перпендикулярных к оси вращения. Точки тела, лежащие на оси вращения, остаются неподвижными. Вращение не является поступательным движением: при вращении оси OO'.
Рис. 9. Вращение бруска вокруг оси OO'. Показаны траектории точек А и B. Суточное движение Земли — вращательное движение. Колебания маятника стенных часов — это тоже вращательное движение. Вращение весьма часто встречается в технике: вращаются колеса, блоки, валы и оси различных механизмов, кривошипные валы, пропеллеры самолетов, стрелки приборов и т. д.
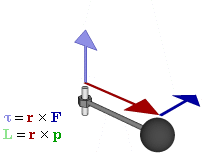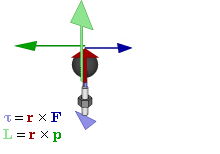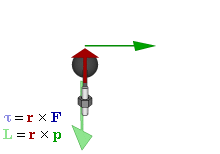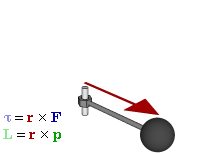
Момент силы. Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) —векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Более точно, момент силы частицы определяется как векторное произведение:
где
Момент силы — производная по времени от момента импульса,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
Момент импульса. Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Момент импульса
где Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
где (В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообщераспределенной системы это может быть записано как В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с. Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:
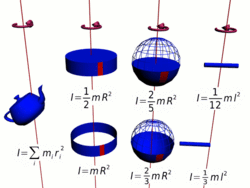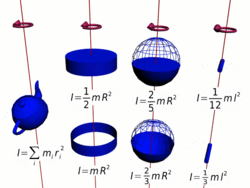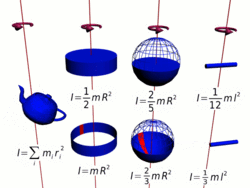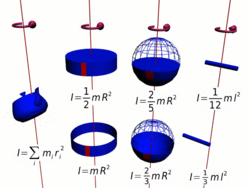
Замечание: в принципе момент импульса может быть вычислен относительно любого начала отсчета (получившиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определенности) его вычисляют относительно центра масс или закрепленной точки вращения твердого тела итп). Момент инерции Момент инерции — скалярная физическая величина, мера инерции тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: § mi — масса i -й точки, § ri — расстояние от i -й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где: § dm = ρ dV — масса малого элемента объёма тела dV, § ρ — плотность, § r — расстояние от элемента dV до оси a. Если тело однородно, то есть его плотность всюду одинакова, то
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.91.173 (0.011 с.) |

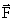 , действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой
, действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой 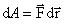 , с другой стороны, d A = –d U, следовательно
, с другой стороны, d A = –d U, следовательно 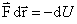 , отсюда
, отсюда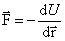 .
.
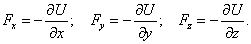
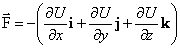 , F = –grad U,
, F = –grad U,
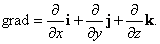 .
.
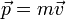 .
.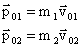
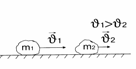
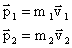
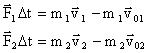
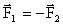 , следовательно:
, следовательно: 
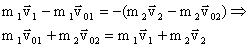

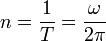 ,
,
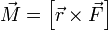
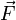 — сила, действующая на частицу, а
— сила, действующая на частицу, а 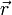 — радиус-вектор частицы.
— радиус-вектор частицы.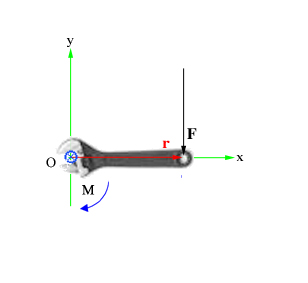 Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Момент силы, приложенный к гаечному ключу. Направлен от зрителя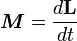 ,
,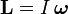
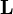 частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса: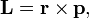
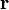 — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,
— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, 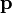 — импульс частицы.
— импульс частицы.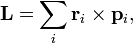
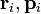 — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.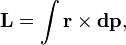 где
где 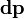 - импульс бесконечно малого точечного элемента системы).
- импульс бесконечно малого точечного элемента системы).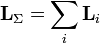 .
.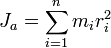 ,
,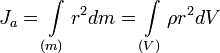 ,
,