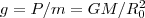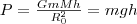Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа и энергия в поле тяготенияСодержание книги
Поиск на нашем сайте
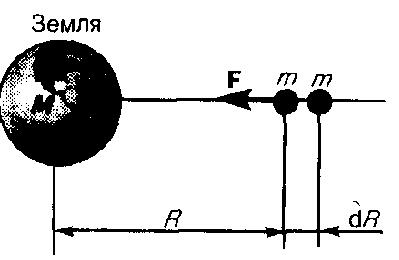
Определим работу, которую совершают силы поля тяготения при перемещении в поле материальной точки массой m. Вычислим, какую надо затратить работу для удаления тела массой m от Земли. На расстоянии R (рис. 1) на тело действует сила
Рис.1
При перемещении этого тела на расстояние dR совершается работа
Знак минус появляется потому, что сила и перемещение в данном случае противоположны по направлению (рис. 1). Если тело перемещать с расстояния R1 до R2, то работа
Из формулы (2) следует, что затраченная работа в поле тяготения не зависит от траектории перемещения, а зависит лишь от начального и конечного положения тела, т. е. силы тяготения действительно консервативны, а поле тяготения является потенциальным. Работа, совершаемая консервативными силами, равна изменению потенциальной энергии системы, взятому со знаком минус, т. е.
Из формулы (2) получаем
Так как в формулы входит только разность потенциальных энергий в двух состояниях, то для удобства принимают потенциальную энергию при R2→∞ равной нулю (P2=0). Тогда (3) запишется в виде P1= -GmM/R1. Поскольку первую точку мы выбрали произвольно, то
Величина
является энергетической характеристикой поля тяготения и называется потенциалом. Потенциал поля тяготения φ - скалярная величина, которая определяется потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность. Таким образом, потенциал поля тяготения, создаваемого телом массой М, равен
где R - расстояние от этого тела до рассматриваемой точки. Из формулы (4) следует, что геометрическое место точек с равными потенциалами образует сферическую поверхность (R=const). Такие поверхности, для которых потенциал постоянен, называются эквипотенциальными. Исследуем взаимосвязь между потенциалом φ поля тяготения и его напряженностью g. Из выражений (1) и (4) вытекает, что элементарная работа dA, совершаемая силами поля при малом перемещении тела массой m, равна
С другой стороны, dA=Fd l (d l - элементарное перемещение). Учитывая (24.1), получаем, что dA=mgd l, т. е. mgd l = -mdφ, или
Величина dφ/d l характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения. Можно показать, что
где В качестве частного примера, исходя из представлений теории тяготения, рассмотрим потенциальную энергию тела, находящегося на высоте h относительно Земли:
где R0 - радиус Земли. Так как
то, учитывая условие h<<R0, получаем
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.123.254 (0.01 с.) |

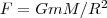
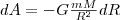 (1)
(1)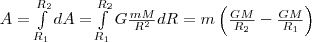 (2)
(2)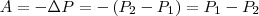
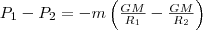 (3)
(3)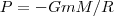
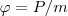
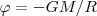 (4)
(4)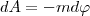
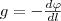
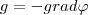 (5)
(5)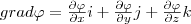 - градиент скаляра φ. Знак минус в формуле (5) показывает, что вектор напряженности g направлен в сторону убывания потенциала.
- градиент скаляра φ. Знак минус в формуле (5) показывает, что вектор напряженности g направлен в сторону убывания потенциала.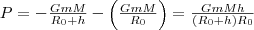
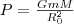 и
и