
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий случай плоского движенияСодержание книги
Поиск на нашем сайте · Основное свойство плоского движения. Вначале сформулируем основное свойство, а затем его докажем. Плоское движение твердого тела можно представить как Из выражений (1) мы видим, что первые два уравнения описывают движение полюса или поступательное движение базовой системы координат Ax*y*, а третье уравнение описывает вращение или угловое движение тела в базовой системе координат, причем вращение происходит вокруг осей Az* и Az1, перпендикулярных плоскости рисунка, и на рис. 79 не показанных. Докажем независимость углового движения тела от поступательного движения, выбрав новый полюс A' (рис. 80). Из-за этого, так как xA'
Сравнительный характер поступательного и вращательного движения. Сравнение поступательного и вращательного движений.
Движение тела складывается из поступательного движения и вращательного движения. Сила, приложенная к центру тяжести, сообщает телу поступательное движение; результирующей вращательный момент сил, не проходящих через центр тяжести, -вращательное движение. Результирующим является в общем случае винтовое движение.
Колебательные движения Колебательные движения - Самый простой случай К. движений уже рассмотрен в статье Гармоническое движение. Такое движение обуславливается переменной силой, во всякий момент направленной противоположно отклонению колеблющейся точки u, пропорциональной величине отклонений. Перемещение колеблющейся точки, в самом простом случае, выражается уравнением: x = α sin2 π t / T, где α размах или амплитуда колебания, T - период одного колебания, t время, считаемое от момента прохождения точки чрез среднее свое положение и угол 2π t / T - фаза колебания. Фаза определяет место точки в пути и считается от 0 до 2π. Кинетическая энергия колеблющейся частицы (масса m), выражаемая, обыкновенно, через ½ mv 2 (живая сила), меняется в течение ½ периода от нуля до некоторого максимума. Поэтому средняя величина энергии для времени ½ периода выражается через π2m a2 / T2. Все возможные типы колебаний могут быть приведены к простому колебанию - гармоническому. Фурье доказал особой теоремой, что всякое периодическое или К. движение с периодом T можно составить через сложение простых - с периодом T, ½ T, ⅓ T, и т.д. и притом составить только одним способом (т. е. с вполне определенными амплитудами и фазами). Иначе говоря, всякое К. движение с периодом Т разлагается на простые гармонические, причем период основного есть Т. Два простых колебания одного периода, следующие по одной и той же прямой, складываются - усиливая или ослабляя друг друга и даже уничтожая (если амплитуды равны, а фазы противоположны, т. е. разнятся на π). Такое явление называется интерференцией колебаний (см. Интерференция). Два колебания одинакового периода, направленные по взаимно перпендикулярным прямым, смотря по амплитудам и разности фаз, складываются или в движение по эллипсу (эллиптическое колебание), или по кругу (круговое колебание), или по прямой. Два колебания различных периодов по взаимно перпендикулярным линиям, в зависимости от амплитуд и разности фаз, складываются в траектории сложных форм, известных под общим именем фигур Лиссажу. Ряд точек, последовательно приходящих в К. движение, называется лучом. Передача колебаний от точки к точке - совершается с определенной скоростью, которая поэтому называется скоростью распространения колебаний. Расстояние между двумя ближайшими точками луча, находящимися в одинаковых фазах колебания, называется длиной волны (λ). Если в ряде точек в некоторый момент (t) перемещение одной точки ряда: x = а sin2 π t / T, то перемещение всякой другой, находящейся в ряде на расстоянии y от первой, выразится уравнением x = a sin2 π (t / T-у / λ). Такое уравнение называется уравнением луча и y называется разностью хода двух колеблющихся точек. Она соответствует разности фаз 2π y / λ
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

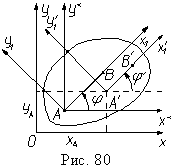 поступательное движение совместно с полюсом и вращение или угловое движение вокруг полюса, причем угловое движение не зависит от поступательного движения.
поступательное движение совместно с полюсом и вращение или угловое движение вокруг полюса, причем угловое движение не зависит от поступательного движения. xA и yA'
xA и yA' 


