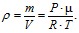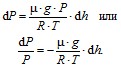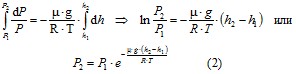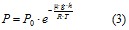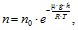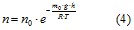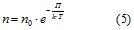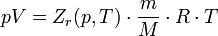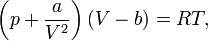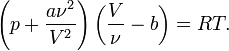Параметрическая формула и распределение Больцмана

Молекулы любого газа находятся в постоянном потенциальном поле тяготения Земли. Тяготение с одной стороны и тепловое движение молекул с другой с другой, приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает. Пологая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова, пусть на высоте h атмосферное давление равно P, тогда на высоте h + dh оно равно P + dP. При dh больше нуля dP должно быть меньше нуля, т.к. давление с высотой убывает.

Разность давлений P и P + dP равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м2, тогда

P– (P + dP) = ρ⋅g⋅dh,

где ρ– плотность газа на высоте h, а изменение dh настолько мало, что плотность газа можно считать постоянной, тогда

dP = –ρ⋅g⋅dh (1)

Из уравнения Менделеева-Клапейрона

Подставим в формулу (1), получим

С изменением высоты от h1 до h2 давление меняется от P1 до P2, тогда

Выражение (2) определяет параметрическую формулу. Если обозначить высоту относительно уровня моря, где давление считается нормальным, тогда выражение (2) можно записать в виде

При P = n⋅k⋅T

где n– концентрация молекул на высоте h. Принимая во внимание, что μ = m0⋅NA, R = k⋅NA, получим

m0⋅g⋅h– это есть потенциальная энергия, тогда

Выражение (5) определяет распределение Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле.

Распределение Максвелла

Реальные газы

Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:

где p — давление; V - объем T — температура; Z_r = Z_r (p,T) — коэффициент сжимаемости газа; m - масса; М —молярная масса; R — газовая постоянная.

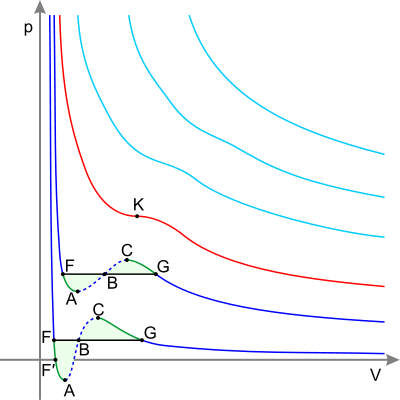
Изотермы реального газа (схематично)

Синие — изотермы при температуре ниже критической. Зелёные участки на них — метастабильные состояния.

Участок левее точки F — нормальная жидкость.
Точка F — точка кипения.
Прямая FG — равновесие жидкой и газообразной фазы.
Участок FA — перегретая жидкость.
Участок F′A — растянутая жидкость (p<0).
Участок AC — аналитическое продолжение изотермы, физически невозможен.
Участок CG — переохлаждённый пар.
Точка G — точка росы.
Участок правее точки G — нормальный газ.
Площади фигуры FAB и GCB равны.

Красная — критическая изотерма.
K — критическая точка.

Голубые — сверхкритические изотермы

 

Уравнение Ван-дер-Ваальса

Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.

Уравнение состояния

Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

где

§ p — давление,

§ V — молярный объём,

§ T — абсолютная температура,

§ R — универсальная газовая постоянная.

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка a учитывает силы притяжения между молекулами (давление на стенку уменьшается, т.к. есть силы, втягивающие молекулы приграничного слоя внутрь), поправка b — силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами).

Для ν молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

где

§ V — объём,