
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа при вращательном движенииСодержание книги
Поиск на нашем сайте
Во всех курсах физики для вычисления работы предлагается формула: dA = FdS cos α (1) Из этой формулы следует, что работа равна нулю, если сила не производит перемещение тела или если сила перпендикулярна перемещению S (например, центростремительные силы). Однако автором в работах [1-3] было показано, что центростремительные и гироскопические силы также совершают работу. В тех же курсах физики приводятся примеры, свидетельствующие о том, что центростремительные силы все же совершают работу! Так, в [4, стр. 257] говорится: «Из того, что при криволинейном движении тело испытывает ускорение, следует, что на него должны действовать силы. Например, грузик, привязанный к нити, может двигаться по окружности только в том случае, если нить тянет его с некоторой силой. Но нить может тянуть грузик только если она деформирована (растянута)». И далее [стр.259]: «При вращении колес, дисков и т.п. возникают деформации того же типа, что и деформации связей, заставляющих тело двигаться по окружности. Именно силы, обусловленные такими деформациями, и сообщают частям вращающегося тела центростремительные ускорения, необходимые для того, чтобы эти части двигались по окружности. Если тела очень жестки, то деформации очень малы и их непосредственное наблюденивенное наблюдени. Однако эти деформации могут привести к разрушению вращающегося тела: в ряде случаев маховики и другие вращающиеся части машин разрывались при движении. Разрушение было связано обычно с превышением допустимой скорости вращения». Вот и говори после этого, что центростремительные силы не совершают работы! Если тело массы m под действием силы F движется по криволинейной траектории dS, то кроме обычной («путевой») работы dA = FdS cos α, еще совершается работа центростремительной силы Fn = man = mV2 / R, где V = dS / dt, dS = R • dφ, где R - радиус кривизны элемента dS (рис.1). Элементарная работа центростремительной силы (см. гл.3) dAn = FndSn (2) Т.к. Sn = R(1 - cos φ), то dSn = R sin φ dφ (3) Рассмотрим, например, разгон тела из неподвижного состояния по дуге окружности радиуса R под действием постоянной силы F, направленной по касательной. Обычная («путевая») работа может быть вычислена по известной формуле dA = M • dφ (4) где M = F • R - момент силы. Поскольку скорость тела определяется выражением V = Rω = Rε t, угловое ускорение ε = F / mR, время t2 = 2φ / ε, то центростремительная сила: Fn = m / R • (Rε t)2 = 2mRεφ = 2φF (5) Элементарная работа центростремительной силы: dAn = 2 FRφ sin φ dφ (6) Работа
Работу An центростремительной силы Fn и обычную («путевую») работу A для различных углов поворота приведем в Таблице 1. Таблица 1. Работа An центростремительной силы Fn и обычная («путевая») работа A для различных углов поворота
Поскольку силы F и Fn взаимноперпендикулярны, то работы этих сил аддитивны, т.е. складываются арифметически: AΣ = A + An. Рассмотрим работу, затрачиваемую на разгон вокруг оси тела вращения (например, цилиндра радиуса R, высотой H, плотность материала цилиндра ρ, масса цилиндра m = πR2 Hρ). На рис. 2 показано сечение цилиндра и действующая на него вращающая сила F. Обычная («путевая») работа определяется формулой (4). Элементарная центростремительная сила, действующая на кольцевой элемент толщиной dr, будет равна
Суммарная центростремительная сила, действующая на цилиндр:
Радиус приложения силы Fn равен R* = 2 R / 3. Тогда в соответствии с выражением (3) получим
Элементарная работа центростремительной силы:
Работа центростремительной силы:
Работа An центростремительной силы Fn и обычная («путевая») работа A вращающей силы F для различных углов поворота приведена в Таблице 2. Таблица 2. Работа An центростремительной силы Fn и обычная («путевая») работа A вращающей
В силу принципа аддитивности суммарная работа на разгон цилиндра находится арифметическим сложением: AΣ = A + An
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

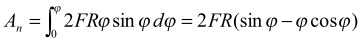 (7)
(7)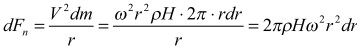 (8)
(8)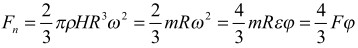 (9)
(9)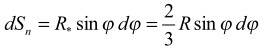 (10)
(10)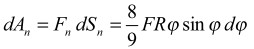 (11)
(11)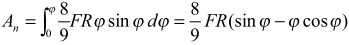 (12)
(12)


