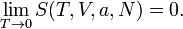Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое толкование энтропииСодержание книги
Поиск на нашем сайте
Рассматривая Вселенную как изолированную систему и распространяя на неё второй закон термодинамики, Р. Клаузиус пришёл к выводу о неизбежности «тепловой смерти» Вселенной, при которой в необозримом будущем в ней будет достигнуто состояние термодинамического равновесия и всякие процессы прекратятся. Этот вывод вызвал много споров, которые не прекращаются до сих пор. Из сказанного в предыдущем разделе следует, что к Вселенной в целом как изолированной системе (F = 0) второе начало термодинамики неприменимо по определению. В силу этого предсказанная Р. Клаузиусом «тепловая смерть» вследствие непрерывного возрастания энтропии ей не угрожает. Понятие энтропии приложимо исключительно к открытым (неизолированным) термодинамическим системам. Напомним, что ни классическая, ни современная термодинамика не отрицают применимости второго начала к изолированным системам и в силу этого принципиально не могут противостоять упомянутому выше утверждению Клаузиуса достаточно решительно. Они опираются на статистическое истолкование второго закона с помощью формулы Больцмана: Таким образом, являясь статистическим законом, второй закон классической термодинамики выражает закономерности хаотического движения большого числа частиц, входящих в состав изолированной системы. Для систем с относительно малымили бесконечнымчислом частиц второй закон термодинамики неприменим: в первом случае из-за возможных значительных флуктуаций, во втором — из-за равновероятности всех микросостояний [5]. Как видим, формулировка второго закона термодинамики, данная Больцманом, содержит в себе указание на относительность (нефундаментальность) этого закона и на недопустимость распространения его на всю Вселенную в целом. В масштабах последней «на отдельных её участках вполне вероятны весьма мощные флуктуации энтропии. На этих участках естественными и самопроизвольными будут те процессы, которые сопровождаются не ростом, а уменьшением энтропии» [4]. «Решив» таким образом проблему тепловой смерти Вселенной, классическая и современная термодинамика одновременно предоставили карт-бланш изобретателям вечных двигателей второго рода. В самом деле, равновесную окружающую среду вполне правомерно представить как систему с бесконечным числом частиц (молекул) и на этом основании игнорировать второй закон термодинамики. С другой стороны, двигатель в масштабах окружающей среды представляет собой систему с относительно малым числом частиц, для которой второй закон термодинамики также неприменим. Возможность отбора теплоты от окружающей среды для выполнения работы оказалась, таким образом, вполне легитимной. Тем более, что для отопления помещений посредством тепловых насосов отбор теплоты от окружающей среды широко практикуется.
Теорема Нерста Теорема Нернста (тепловая теорема Нернста) - утверждение, являющееся одной из формулировок третьего начала термодинамики, сформулированное Вальтером Нернстом в 1906 году как обобщение экспериментальных данных по термодинамике гальванических элементов. Теорема Нернста утверждает, что всякий термодинамический процесс, протекающий при фиксированной температуре T в сколь угодно близкой к нулю, Макс Планк в 1910 году сформулировал более жесткое утверждение: величина S 0 была конечной и S 0 = 0. В формулировке Планка теорема Нернста имеет вид начального (граничного или предельного) условия для системы дифференциальных уравнений определяющих энтропию: При выключении температуры,
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.24.176 (0.01 с.) |

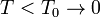 , не должен сопровождаться изменением энтропии S, то есть изотерма T = 0 совпадает с предельной адиабатой S 0.
, не должен сопровождаться изменением энтропии S, то есть изотерма T = 0 совпадает с предельной адиабатой S 0.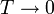 , энтропия термодинамической системы также стремится к нулю:
, энтропия термодинамической системы также стремится к нулю: