
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное уравнение динамики вращательного движенияСодержание книги
Поиск на нашем сайте
Основое уравнение динамики вращательного движения материальной точки - угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.
М = E*J или E = M/J
Сравнивая полученное выражение со вторым законом Ньютона с поступательным законом, видим, что момент инерции J является мерой инертности тела во вращательном движении. Как и масса величина аддитивная.
Момент инерции тонкого кольца:
Зако́н сохране́ния моме́нта Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем. Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.
Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения.
Гироскопический эффект Гироскопом (или волчком) называют массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии (рис.5.5).
Момент количества движения гироскопа совпадает с его осью вращения. Для того, чтобы изменитьнаправление в пространстве оси гироскопа, т.е. направление вектора
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.199.54 (0.009 с.) |


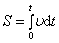 отсюда
отсюда 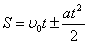 или
или 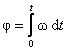 .
.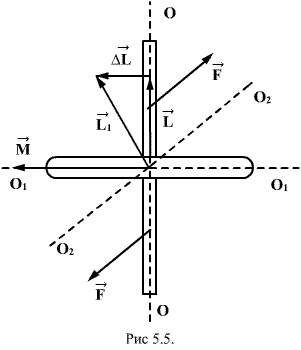
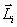 необходимо в соответствие основным уравнением динамики вращательного движения
необходимо в соответствие основным уравнением динамики вращательного движения 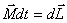 подействовать на него моментом внешних сил
подействовать на него моментом внешних сил 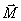 . Пусть это пара сил
. Пусть это пара сил 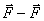 создающая вращающий момент относительно оси
создающая вращающий момент относительно оси 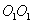 , лежащей в плоскости чертежа перпендикулярно оси ОО (вращение вокруг
, лежащей в плоскости чертежа перпендикулярно оси ОО (вращение вокруг 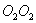 перпендикулярно к этим осям (т.е. к ОО и
перпендикулярно к этим осям (т.е. к ОО и 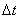 момент количества движения гироскопа
момент количества движения гироскопа 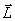 получит приращение
получит приращение 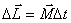 , которое имеет такое же направление, как и
, которое имеет такое же направление, как и  , лежащей в плоскости чертежа. Направление вектора
, лежащей в плоскости чертежа. Направление вектора 


