
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смещение, скорость, ускорение, фаза, начальная фаза колебательного движения.Содержание книги
Поиск на нашем сайте Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку. Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения метр.(амлитудная дисмортинографная отклонненость тела от заданого направления). Скорость:
Ускорение колебаний:
Фаза: Фа́за колеба́ний — физическая величина, при заданной амплитуде и коэффициенте затухания, определяющая состояние колебательной системы в любой момент времени.[1] Если колебания системы описываются синусоидальным (косинусоидальным) или экспоненциальным законами: A cos(ω t + φ0), A sin(ω t + φ0),
то фаза колебаний определяется как аргумент периодической функции, описывающей гармоническийколебательный процесс (ω— угловая частота (чем величина выше, тем на большее значение изменяется угол за ед. времени), t — время, φ0— (угол в начале колебаний) начальная фаза колебаний, то есть фаза колебаний в начальный момент времени t = 0). Фаза обычно выражается в угловых единицах (радианах, градусах) или в циклах (долях периода): 1 цикл = 2π радиан = 360 градусов.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

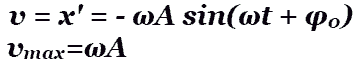

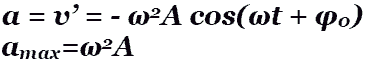
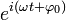 ,
, 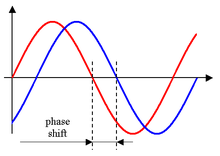 Иллюстрация смещения по фазе волны в четверть фазы.
Иллюстрация смещения по фазе волны в четверть фазы.


