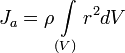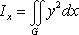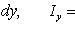Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика криволинейного движенияСодержание книги
Поиск на нашем сайте
МЕХАНИКА Полное ускорение Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника). Направление полного ускорения также определяется правилом сложения векторов:
Кривизна траектории. Траекто́рия материа́льной то́чки — линия в трёхмерном пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве. Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения. Кроме того, и при наличии движущегося по ней объекта, траектория сама по себе не может ничего дать в отношении причин движения, то есть о действующих силах.
Вращательное движение Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.
Вращательное движение тела в зависимости от времени t характеризуют угловые величины: φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек2). Закон вращательного движения тела выражается уравнением φ = f (t). Радиус вектор Ра́диус-ве́ктор (обычно обозначается Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку. Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.
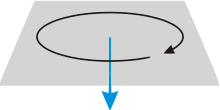
На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки. Угловая скорость, ускорение Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду.
Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела. При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно:
Вектор углового ускорения α направлен вдоль оси вращения (в сторону При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени[2], то есть
и направлен по касательной к годографу вектора Существует связь между тангенциальным и угловым ускорениями:
где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/сек2.
Динамика Законы Ньютона § 1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
§ 2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).
В наиболее общем случае, который описывает также движение тела с изменяющейся массой (например, реактивное движение), 2-й закон Ньютона принято записывать следующим образом:
где § 3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса
Принцип относительности Галилея
Из формулы для ускорений следует, что если движущаяся система отсчета движется относительно первой без ускорения, то есть Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль (см.второй закон Ньютона), то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел (а не их положения относительно абстрактного начала отсчета), окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-то конкретной из инерциальных систем отсчета. Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея, в отличие от Принципа относительности Эйнштейна Иным образом этот принцип формулируется (следуя Галилею) так: если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым. Требование (постулат) принципа относительности вместе с преобразованиями Галилея, представляющимися достаточно интуитивно очевидными, во многом следует форма и структура ньютоновской механики (и исторически также они оказали существенное влияние на ее формулировку). Говоря же несколько более формально, они налагают на структуру механики ограничения, достаточно существенно влияющие на ее возможные формулировки, исторически весьма сильно способствовавшие ее оформлению. Осмотическое давление Силы Ван-дер-Ваальса — электромагнитные межмолекулярные силы, возникающие при поляризации молекул и образовании диполей. Ван-дер-Ваальсовы силы быстро убывают с увеличением расстояния. Сила инерции — фиктивная сила, вводимая в неинерциальных системах отсчёта для того, чтобы в них выполнялся второй закон Ньютона. В частности, в системе отсчёта, связанной с равноускоренно движущимся телом сила инерции направлена противоположно ускорению. Из полной силы инерции могут быть для удобства выделены центробежная сила и сила Кориолиса. Поле Сил Силовые поля Экспериментально установлено, что Третий закон Ньютона «сила противодействия равна силе действия» выполняется не только при непосредственном контакте взаимодействующих тел. Открытый Ньютоном Закон всемирного тяготения отражает реально существующее и фундаментальное свойство Природы, в которой существует действие на расстоянии. В простейшем случае он может быть сведён к взаимодействию только двух тел, любое из которых, удобства ради, может рассматриваться как источник силы, а второе - как объект её воздействия. В случае гравитации эти тела взаимодействуют непосредственно своими массами, а в случае, если взаимодействие носит электрический характер, то к этому добавляется и взаимодействие несущих их зарядов. Но, поскольку заряд, как таковой, не существует независимо от несущего его тела, то электрическое взаимодействие тел проявляется в виде той же рассматриваемой в механике силы, служащей причиной ускорения.
В современной физике принята концепция близкодействия, в соответствие с которой всякое действие на расстоянии должно осуществляться при помощи тех или иных посредников. В роли этого посредника выступает силовое поле, порождаемое обоими телами. Возможна ситуация, что массы взаимодействующих тел (или же их заряды) существенно отличаются друг от друга по своей величине. В таком случае может оказаться, что появившееся в их окрестности третье тело будет испытывать взаимодействие с первым, независимо от изменения свойств второго, которое может и вообще исчезнуть. Это будет свидетельством того, что в исходном случае второе тело, рассматриваемое изначально как объект взаимодействия, своим присутствием с заданной степенью приближения не влияет на поле первого тела и потому может рассматриваться как «пробный объект», служащий как для обнаружения поля источника силы, так и его количественной оценки. В макроскопических масштабах современной физике известны два вида полей: поле гравитации и поле электромагнитное. Но, поскольку магнитные силы сводятся к движению в системе отсчёта наблюдателя зарядов (т.е. к токам), создающих в общем случае переменное электрическое поле, в качестве пробных объектов для измерения этих полей используется либо масса m, либо масса, несущая заряд q Для детального описания силового взаимодействия тел в физике повсеместно принята стратегия первоначального рассмотрения задачи в наиболее упрощенной - дифференциальной форме, позволяющей отвлечься от учёта размеров взаимодействующих объектов и расстояния между ними, а затем переходу к суммированию полученных результатов в интегральной форме с учётом реальной геометрии явления. Справедливость такого подхода основана на экспериментально установленном законе независимости сил, действие каждой из которых на объект не зависит от действия на него других сил. Следствием этого является правило параллелограмма, используемое для векторного сложения нескольких сил различного направления и величины.
Чрезвычайно популярным в Физике является понятие о физической точке, т.е. о таком объекте, размеры которого настолько малы, что могут не приниматься во внимание, но остальные его параметры, в первую очередь масса, имеют реальную и достаточную для их учёта величину. В разделе Физики - Оптике тот же смысл вкладывается в понятие о точечном объекте, т.е. об объекте, угловые размеры которого α из точки его наблюдения не превышают заданной малой величины. Для грубых оценок достаточно, чтобы поперечные размеры объекта не менее, чем в 10 раз были меньше расстояния его наблюдения т.е. (α <<0,1 рад). Для более точных оценок эта величина составляет 0,01 рад и менее.
Электростатическое поле (поле неподвижных зарядов) Применительно к электростатическому взаимодействию двух «точечных зарядов» используется закон Кулона. В скалярном представлении закон Кулона для двух взаимодействующих зарядов записывается следующим образом: F 1,2 = Здесь F 1,2 есть сила взаимодействия первого и второго заряда, считающаяся положительной, если заряды отталкиваются, q 1 и q 2 есть, соответственно, первый и второй заряды, взятые алгебраически (с их знаком), r 1,2 -расстояние между ними, а k — коэффициент пропорциональности. Таким образом, закон указывает, что одноименные заряды отталкиваются (а разноименные – притягиваются). Закон Кулона определяет взаимодействие двух неподвижных точечных заряда в воздухе. В физическом вакууме действие закона Кулона не проверялось. Поэтому использование Закона Кулона для модели строения атома Резерфорда и модели электромагнитного поля Максвела является некорректным. В СГСЭ единица измерения заряда выбрана таким образом, что коэффициент k = 1 и, как правило, опускается. В СИ k ≈ 8,987551787 109 Н м^2 / Кл^2 Поскольку электростатическое поле создаётся и уединённым электрическим зарядом, целесообразно ввести для его (поля) количественного описание понятие о его напряжённости. Напряжённость E электростатического поля заряда q 1 измеряется силой F 1,2, с которой оно действует или действовало бы на единичный заряд, находящийся на расстоянии r 1,2 от этого заряда: E =
Гравитационное поле Применительно к гравитационному взаимодействию двух «точечных масс» используется закон Всемирного тяготения Ньютона.
В скалярном представлении этот закон для двух взаимодействующих масс в любой среде записывается следующим образом: F 1,2 =
G — фундаментальная гравитационная постоянная, равная Для описания интенсивности поля тяготения термин "напряжённость" поля не используется. Вместо него используется термин "Ускорение свободного падения", которое по аналогии с электрическим полем вычисляется по формуле: g = Это- тоже вектор, направленный в сторону притягивающего тела. Между гравитационными и электрическими силами существует, как считал Эйнштейн, связь. Об этом говорит квадратичный характер зависимости интенсивностей его полей. Существует мнение, что именно это предопределяет трёхмерность пространства, в котором происходят все физические явления. Электромагнитное поле, постоянное во времени (поле постоянных токов) Силовое взаимодействие между электрическими зарядами, не находящимися в движении относительно друг друга описывается законом Кулона. Однако заряды, находящиеся в движении относительно друг друга создают магнитные поля, посредством которых созданные движением зарядов токов в общем случае приходят в состояние силового взаимодействия. Принципиальным отличием силы, возникающей при относительном движении зарядов от случая их стационарного размещения, является различие в геометрии этих сил. Для случая электростатики сил взаимодействия двух зарядов направлена по линии, их соединяющей. Поэтому геометрия задачи двумерна и рассмотрение ведётся в плоскости, проходящей через эту линию. В случае токов сила, характеризующая магнитное поле, создаваемое током, расположена в плоскости, перпендикулярной току. Поэтому картина явления становится трёхмерной.Магнитное поле, создаваемое бесконечно малым по длине элементом первого тока, взаимодействуя с таким же элементом второго тока, в общем случае создаёт силу, действующую на него. При этом для обех токов эта картина полностью симметрична в том смысле, что нумерация токов произвольна. Закон взаимодействия токов используется для эталонирования постоянного электрического тока.Он является следствием закона Био-Савра-Лапласа, устанавливающего зависимость величины вектора магнитной индукции от силы тока, текущего по проводнику, и расстояния до точки наблюдения. Взаимодействие магнитных полей двух проводников проявляется в виде силы, стемящейся изменить взаимное расположение проводников. В случае, если проводники параллельны друг другу и по ним текут токи I 1 и I 2, а сами проводники находятся на расстоянии r 1,2, то элемент длины первого проводника dl 1действует на элемент длины второго проводника dl 2 и наоборот с силой: dF = k где в системе Си коэффициент k = Пример Уравнение Энергия и работа. (теорема о Ек) Энергия является мерой способности физической системы совершить работу, поэтому количественно энергия и работа выражаются в одних единицах. Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени. Это утверждение носит название закона сохранения энергии. Работа и Энергия Термин "работа" в механике имеет два смысла: работа как процесс, при котором сила перемещает тело, действуя под углом, отличном от 90°; работа - физическая величина, равная произведению силы, перемещения и косинуса угла между направлением действия силы и перемещением: А = Fs cos a. Работа равна нулю, когда тело движется по инерции (F = 0), когда нет перемещения (s = 0) или когда угол между перемещением и силой равен 90° (cos а = 0). Единицей работы в СИ служит джоуль (Дж). 1 джоуль - это такая работа, которая совершается силой 1 Н при перемещении тела на 1 м по линии действия силы. Для определения быстроты совершения работы вводят величину "мощность". Мощность равняется отношению совершенной работы ко времени, за которое она выполнена:
Единицей мощности в СИ служит 1 ватт (Вт). 1 Вт - мощность, при которой совершается работа в 1 Дж за 1 секунду. Рассмотрим действие на тело некоторой постоянной силы F. На участке пути s будет произведена работа А. В результате у тела изменится скорость:
Величину
Кинетическая энергия - энергия движения, ею обладают все движущиеся тела. Эта величина является относительной, то есть она изменяется в зависимости от выбранной системы отсчета. Кроме этого вида механической энергии, существует и другой ее вид - потенциальная энергия. Рассмотрим систему двух взаимодействующих тел. Например, тела, поднятого над Землей, и саму Землю. Работа силы тяжести при перемещении тела на отрезке |h1 - h2| будет равна:
Величину mgh в соответствующей точке, которая расположена на высоте h, называют потенциальной энергией тела, находящегося в поле тяжести. Из предыдущего уравнения вытекает, что работа не зависит от траектории движения в доле силы тяжести, а определяется лишь изменением высоты. Потенциальная энергия характеризует и другие взаимодействующие тела. Так, потенциальной энергией обладает сжатая пружина:
где k - модуль упругости, х - смещение от положения равновесия. Потенциальная энергия, как и кинетическая, является величиной относительной, поскольку и высота, и смещение зависят от выбора точки отсчета. Теорема о кинетической энергии: работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела. Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях. Если начальная скорость движения тела массой т равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела: Физический смысл кинетической энергии: кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость. Работа переменной силы.
Рассмотрим материальную точку, движущуюся под действием силы Р по прямой. Если действующая сила постоянна и направлена вдоль прямой, а перемещение равно s, то, как известно из физики, работа А этой силы равна произведению Ps. Теперь выведем формулу для подсчета работы, совершаемой переменной силой.
Пусть точка движется по оси Ох под действием силы, проекция которой на ось Ох есть функция f от х. При этом мы будем предполагать, что f есть непрерывная функция. Под действием этой силы материальная точка переместилась из точки М (а) в точку М (b) (рис. 1, а). Покажем, что в этом случае работа А подсчитывается по формуле
Разобьем отрезок [а; b] на п отрезков одинаковой длины
и точность приближенного равенства тем выше, чем короче отрезки, на которые разбит отрезок [а;b] Естественно, что это приближенное равенство переходит в точное, если считать, что n→∞:
Поскольку An при n →∞ стремится к интегралу рассматриваемой функции от а до b, формула (1) выведена.
Рис.1
При перемещении этого тела на расстояние dR совершается работа
Знак минус появляется потому, что сила и перемещение в данном случае противоположны по направлению (рис. 1). Если тело перемещать с расстояния R1 до R2, то работа
Из формулы (2) следует, что затраченная работа в поле тяготения не зависит от траектории перемещения, а зависит лишь от начального и конечного положения тела, т. е. силы тяготения действительно консервативны, а поле тяготения является потенциальным. Работа, совершаемая консервативными силами, равна изменению потенциальной энергии системы, взятому со знаком минус, т. е.
Из формулы (2) получаем
Так как в формулы входит только разность потенциальных энергий в двух состояниях, то для удобства принимают потенциальную энергию при R2→∞ равной нулю (P2=0). Тогда (3) запишется в виде P1= -GmM/R1. Поскольку первую точку мы выбрали произвольно, то
Величина
является энергетической характеристикой поля тяготения и называется потенциалом. Потенциал поля тяготения φ - скалярная величина, которая определяется потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность. Таким образом, потенциал поля тяготения, создаваемого телом массой М, равен
где R - расстояние от этого тела до рассматриваемой точки. Из формулы (4) следует, что геометрическое место точек с равными потенциалами образует сферическую поверхность (R=const). Такие поверхности, для которых потенциал постоянен, называются эквипотенциальными. Исследуем взаимосвязь между потенциалом φ поля тяготения и его напряженностью g. Из выражений (1) и (4) вытекает, что элементарная работа dA, совершаемая силами поля при малом перемещении тела массой m, равна
С другой стороны, dA=Fd l (d l - элементарное перемещение). Учитывая (24.1), получаем, что dA=mgd l, т. е. mgd l = -mdφ, или
Величина dφ/d l характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения. Можно показать, что
где В качестве частного примера, исходя из представлений теории тяготения, рассмотрим потенциальную энергию тела, находящегося на высоте h относительно Земли:
где R0 - радиус Земли. Так как
то, учитывая условие h<<R0, получаем
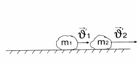
Закон сохранения импульса Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная суммаимпульсов всех тел (или частиц) замкнутой системы есть величина постоянная.
Вращательное движение Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна. При равномерном вращении (T оборотов в секунду), Частота вращения — число оборотов тела в единицу времени.
Период вращения — время одного полного оборота. Период вращения T и его частота ν связаны соотношением T = 1 / ν.
При вращательном движении все точки тела движутся по окружностям, центры которых лежат на прямой. Эту прямую называют осью вращения (прямая 00' на рис.9). Окружности лежат в парал-лельных плоскостях, перпендикулярных к оси вращения. Точки тела, лежащие на оси вращения, остаются неподвижными. Вращение не является поступательным движением: при вращении оси OO'.
Рис. 9. Вращение бруска вокруг оси OO'. Показаны траектории точек А и B. Суточное движение Земли — вращательное движение. Колебания маятника стенных часов — это тоже вращательное движение. Вращение весьма часто встречается в технике: вращаются колеса, блоки, валы и оси различных механизмов, кривошипные валы, пропеллеры самолетов, стрелки приборов и т. д.
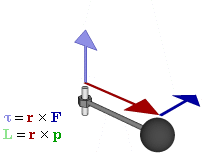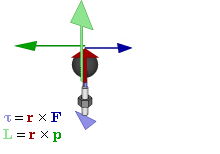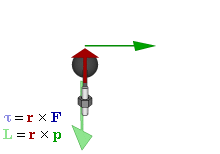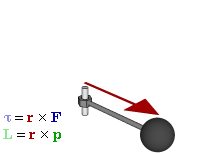
Момент силы. Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) —векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Более точно, момент силы частицы определяется как векторное произведение:
где
Момент силы — производная по времени от момента импульса,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
Момент импульса. Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Момент импульса
где Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
где (В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообщераспределенной системы это может быть записано как В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с. Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:
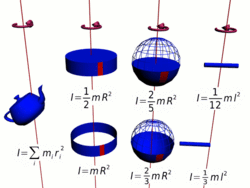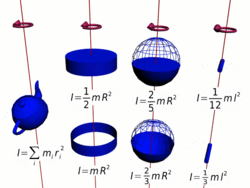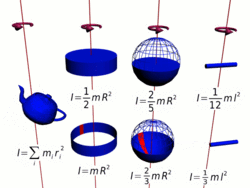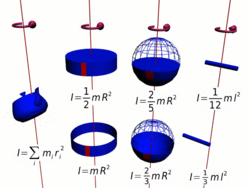
Замечание: в принципе момент импульса может быть вычислен относительно любого начала отсчета (получившиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определенности) его вычисляют относительно центра масс или закрепленной точки вращения твердого тела итп). Момент инерции Момент инерции — скалярная физическая величина, мера инерции тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: § mi — масса i -й точки, § ri — расстояние от i -й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где: § dm = ρ dV — масса малого элемента объёма тела dV, § ρ — плотность, § r — расстояние от элемента dV до оси a. Если тело однородно, то есть его плотность всюду одинакова, то
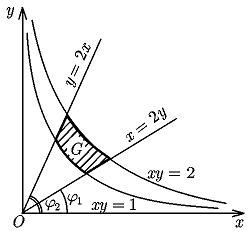
Пример, вычисления Найти моменты инерции Ix и Iy относительно осей Ox и Oy пластины с плотностью ρ = 1, ограниченной кривыми xy = 1, xy = 2, y = 2 x, x = 2 y и расположенной в I квадранте.
Решение. Данная пластинка G изображена на рисунке
По формулам для Ix и Iy имеем
| |||||||||||||||
|
| Поделиться: |

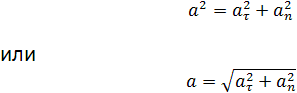
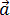 =
= 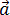 τ +
τ + 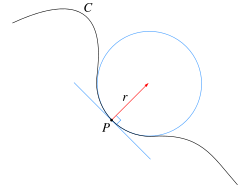
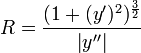 формула радиуса кривизны
формула радиуса кривизны
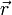 или просто
или просто 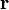 ) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.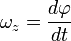 ,
,
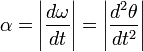
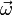 при ускоренном вращении и противоположно
при ускоренном вращении и противоположно 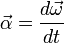 ,
,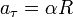 ,
,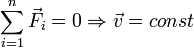
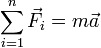
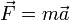
 ,
,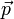 — импульс тела. Таким образом, сила характеризует быстроту изменения импульса.
— импульс тела. Таким образом, сила характеризует быстроту изменения импульса.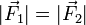
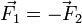
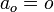 , то ускорение
, то ускорение 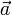 тела относительно обеих систем отсчета одинаково.
тела относительно обеих систем отсчета одинаково.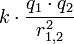
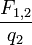
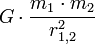
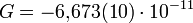 м³/(кг с²) Знак минус означает, что сила, действующая на тела, всегда направленной в сторону сближения тяготеющих тел.
м³/(кг с²) Знак минус означает, что сила, действующая на тела, всегда направленной в сторону сближения тяготеющих тел.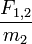
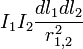 ,
,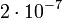 Н /А^2
Н /А^2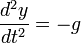 описывает движение тела в поле земного тяготения. Ему удовлетворяет любая квадратичная функция вида y (t) = − gt 2 / 2 + at + b, где a, b — произвольные числа. Для выделения конкретного закона движения необходимо указать начальную координату тела и его скорость, то есть начальные условия.
описывает движение тела в поле земного тяготения. Ему удовлетворяет любая квадратичная функция вида y (t) = − gt 2 / 2 + at + b, где a, b — произвольные числа. Для выделения конкретного закона движения необходимо указать начальную координату тела и его скорость, то есть начальные условия.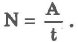
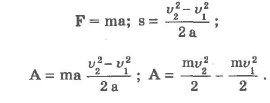
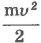 для материальной точки называют кинетической энергией тела.
для материальной точки называют кинетической энергией тела.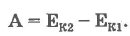
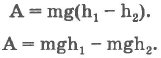
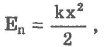
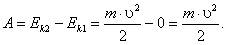
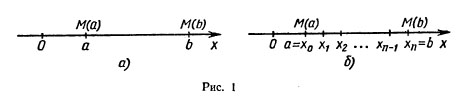
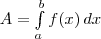 (1)
(1)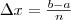 .Это отрезки [а; x1], [x1; x2],..., [xn-1;b] (рис. 1,6). Работа силы на всем отрезке [а; b] равна сумме работ этой силы на полученных отрезках. Так как f есть непрерывная функция от x, при достаточно малом отрезке [а; x1] работа силы на этом отрезке приблизительно равна f (а) (x1—а) (мы пренебрегаем тем, что f на отрезке меняется). Аналогично работа силы на втором отрезке [x1; x2] приближенно равна f (x1) (x2 — x1) и т. д.; работа силы на n-ом отрезке приближенно равна f (xn-1)(b — xn-1). Следовательно, работа силы на всем отрезке [а; b] приближенно равна:
.Это отрезки [а; x1], [x1; x2],..., [xn-1;b] (рис. 1,6). Работа силы на всем отрезке [а; b] равна сумме работ этой силы на полученных отрезках. Так как f есть непрерывная функция от x, при достаточно малом отрезке [а; x1] работа силы на этом отрезке приблизительно равна f (а) (x1—а) (мы пренебрегаем тем, что f на отрезке меняется). Аналогично работа силы на втором отрезке [x1; x2] приближенно равна f (x1) (x2 — x1) и т. д.; работа силы на n-ом отрезке приближенно равна f (xn-1)(b — xn-1). Следовательно, работа силы на всем отрезке [а; b] приближенно равна: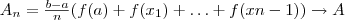
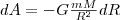 (1)
(1)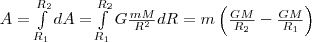 (2)
(2)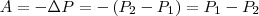
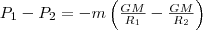 (3)
(3)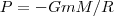
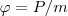
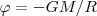 (4)
(4)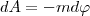
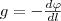
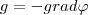 (5)
(5)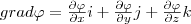 - градиент скаляра φ. Знак минус в формуле (5) показывает, что вектор напряженности g направлен в сторону убывания потенциала.
- градиент скаляра φ. Знак минус в формуле (5) показывает, что вектор напряженности g направлен в сторону убывания потенциала.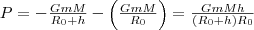
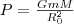 и
и 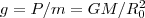
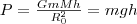
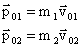
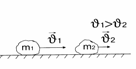
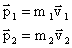
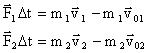
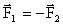 , следовательно:
, следовательно: 
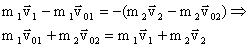

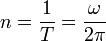 ,
,
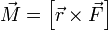
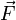 — сила, действующая на частицу, а
— сила, действующая на частицу, а 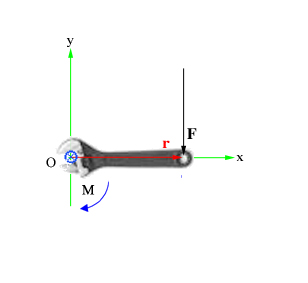 Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Момент силы, приложенный к гаечному ключу. Направлен от зрителя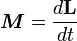 ,
,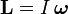
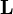 частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса: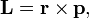
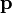 — импульс частицы.
— импульс частицы.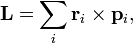
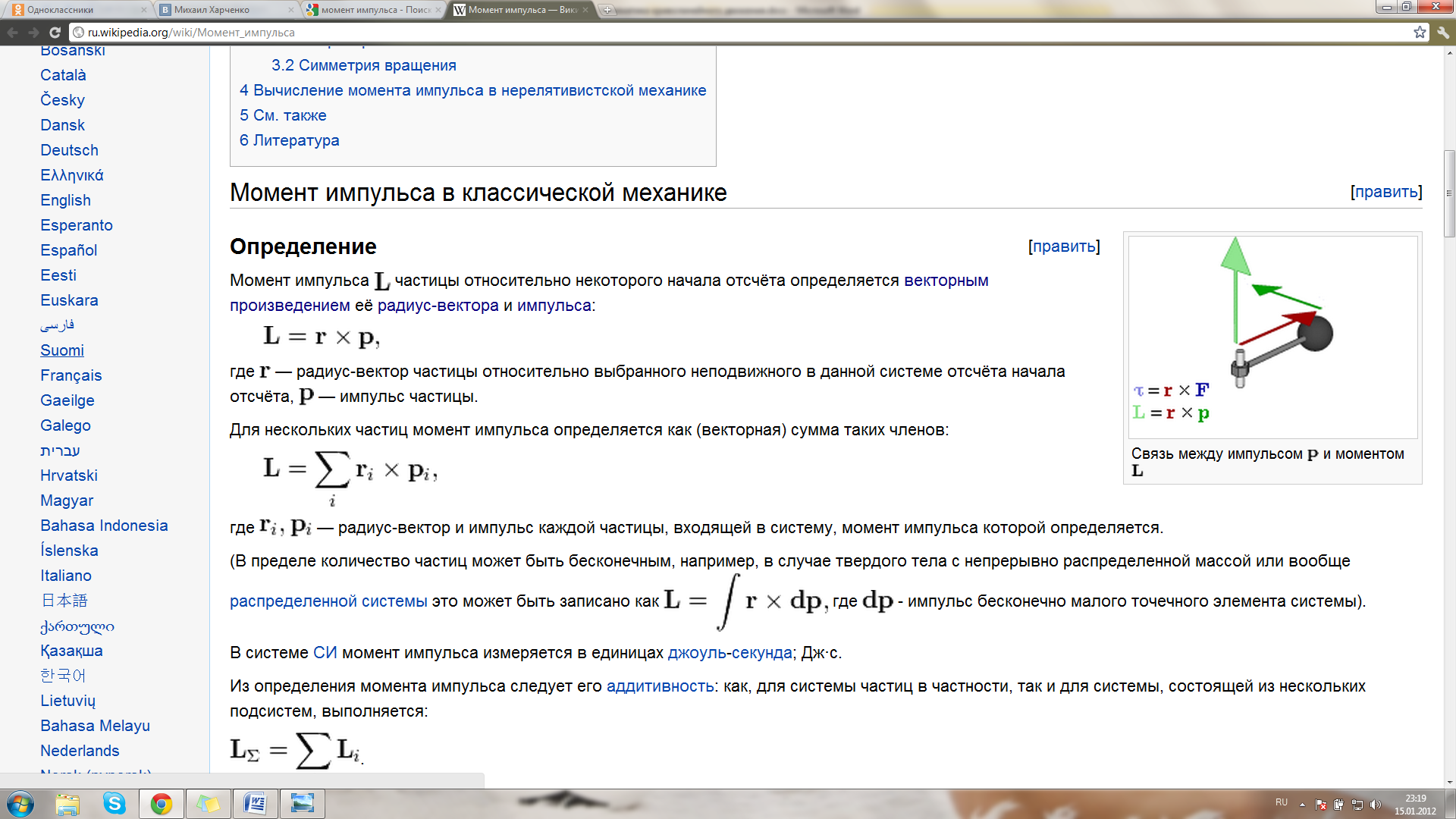
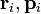 — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.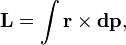 где
где 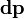 - импульс бесконечно малого точечного элемента системы).
- импульс бесконечно малого точечного элемента системы).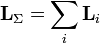 .
.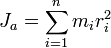 ,
,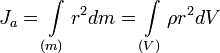 ,
,