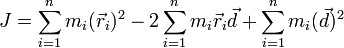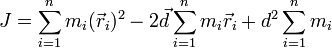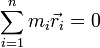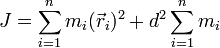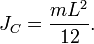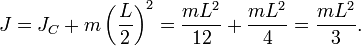Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
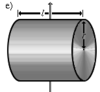
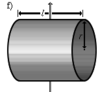
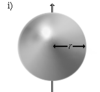
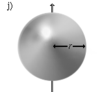
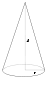
Осевые моменты инерции некоторых телСодержание книги
Поиск на нашем сайте
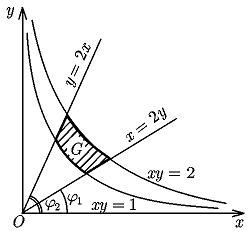
Пример, вычисления Найти моменты инерции Ix и Iy относительно осей Ox и Oy пластины с плотностью ρ = 1, ограниченной кривыми xy = 1, xy = 2, y = 2 x, x = 2 y и расположенной в I квадранте.
Решение. Данная пластинка G изображена на рисунке
По формулам для Ix и Iy имеем
Чтобы свести каждый из этих двойных интегралов к повторному, нужно область G разбить на три части. Удобнее перейти к полярным координатам: x = ρ cos φ, y = ρ sin φ. Тогда φ изменяется от
Аналогично получаем
Теорема Штейнера Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса):момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела JC относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
JC — известный момент инерции относительно оси, проходящей через центр масс тела, J — искомый момент инерции относительно параллельной оси, m — масса тела, d — расстояние между указанными осями. [править]Вывод Момент инерции, по определению:
Радиус-вектор
где
Вынося за сумму
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:
Тогда:
Откуда и следует искомая формула:
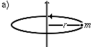
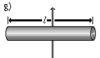
где JC — известный момент инерции относительно оси, проходящей через центр масс тела. [править]Пример Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью C) равен
Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен
где d — расстояние между искомой осью и осью C. В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формуле d = L / 2:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.88.246 (0.009 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

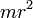


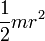

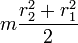
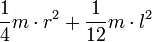
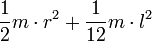
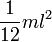

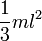
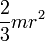
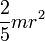
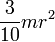
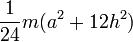
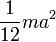
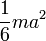
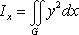
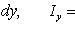

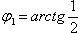 до
до 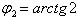 (см. рисунок), а при каждом значении φ из сегмента [ φ 1, φ 2] переменная ρ изменяется от
(см. рисунок), а при каждом значении φ из сегмента [ φ 1, φ 2] переменная ρ изменяется от 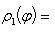
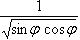 (значение ρ на кривой xy = 1, уравнение которой в полярных координатах в I квадранте имеет вид
(значение ρ на кривой xy = 1, уравнение которой в полярных координатах в I квадранте имеет вид 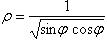 ) до
) до 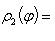
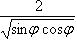 (значение ρ на кривой xy = 2). Следовательно,
(значение ρ на кривой xy = 2). Следовательно,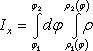
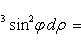
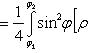
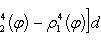
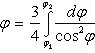

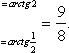
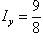 .
.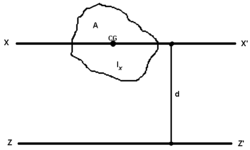 Иллюстрация теоремы для момента площади.
Иллюстрация теоремы для момента площади. где
где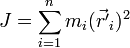
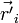 можно расписать как разность двух векторов:
можно расписать как разность двух векторов: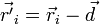 ,
,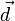 — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:
— радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид: