Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведенная теплота и теорема КлаузисаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Из рассмотренного цикла Карно (п. 5.4) видно, что равны между собой отношения теплот к температурам, при которых они были получены или отданы в изотермическом процессе:
Отношение теплоты Q в изотермическом процессе к температуре, при которой происходила передача теплоты, называется приведенной теплотой
Для подсчета приведенной теплоты в произвольном процессе необходимо разбить этот процесс на бесконечно малые участки, где Т можно считать константой. Приведенная теплота на таком участке будет равна
Тогда в обратимом цикле Карно (п. 5.3, 5.4) имеем:
Этот результат справедлив для любого обратимого процесса.
Из равенства нулю интеграла, взятого по замкнутому контуру, следует, что подынтегральное выражение
Функция состояния, полный дифференциал которой равен Для обратимых процессов изменение энтропии, как следует из (6.1.2),
Энтропия Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.
где dS — приращение энтропии; δ Q — минимальная теплота, подведенная к системе; T — абсолютная температура процесса;
Из теоремы Клаузиуса следует, что приведенная теплота подобно энергии (потенциальной, внутренней) является функцией состояния (не зависит от пути перехода и зависит только от состояния системы). Независимость интеграла
от пути перехода означает, что этот интеграл выражает собой изменение некоторой функции состояния системы, она называется энтропия и обозначается буквой S. Изменение энтропии системы, очевидно, равно
Мы говорим только об изменении энтропии (подобно изменению потенциальной энергии
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.35.147 (0.01 с.) |

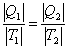 .
.
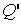 :
: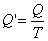 .
.
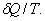
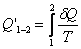 .
.
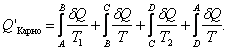
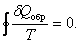
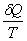 есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Это позволяет ввести новую функцию состояния S:
есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Это позволяет ввести новую функцию состояния S: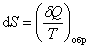 .
.
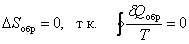 .
.
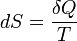 ,
,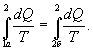
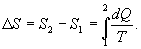
 , для которой не важно где начало отсчета). Из уравнения (9.30) вытекает основное количественное выражение второго начала термодинамики
, для которой не важно где начало отсчета). Из уравнения (9.30) вытекает основное количественное выражение второго начала термодинамики