
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параллельное соединение трубопроводов.Содержание книги
Поиск на нашем сайте
Из рис. 6.7 видно, что в узловой точке А поток жидкости в магистрали делится на четыре потока в ветвях 1–4, которые объединяются в точке В, образуя далее продолжение магистрального трубопровода.
Рис. 6.7 Основной задачей является определение расхода каждой ветки Решение задачи основано на том, что напоры
представляет одну и ту же потерю напора hv одновременно для каждой из веток. Учитывая, что
можно записать следующую систему равенств:
В системе (6.31) имеем (для каждого их трех выражений Для замыкания системы (6.31) требуется ещё одно уравнение, которое может быть уравнением узловых расходов, а именно:
Рассмотрим определение неизвестных величин с учетом выражений Выразим расходы
В соответствии с системой равенств (6.33), получим
Из выражений (6.34) находим расход
Значения Q 2, Q 3, и Q 4 найдём из выражений (6.34). Потерянный напор H находится по одному из равенств (6.31), например:
В водопроводных сетях потери напора на местные сопротивления, кроме некоторых случаев, незначительны по сравнению с линейными потерями. Поэтому при большом напоре их не принимают во внимание. При расчёте внутренних водопроводов на линейные потери напора вводят поправочный коэффициент K M, учитывающий местные сопротивления:
Только при очень ограниченном напоре местные сопротивления определяются расчётом. Такой случай может быть, например, при питании внутреннего водопровода от бака, установленного в здании. Расчёт потерь производится по формуле
Из уравнения расхода выразим скорость
Она выражает суммарные сопротивления в трубопроводе длиной l при единичном расходе. Принимая с некоторой погрешностью
или
Отсюда
Из формулы (6.40) следует, что диаметры труб изменяются обратно пропорционально корню четвёртой степени из величины напора или потерь напора. Пусть напор увеличился в 2 раза:
Новый расчётный диаметр d 1 будет на 16% меньше предыдущего d.
7. ОСНОВЫ ТЕОРИИ ПОДОБИЯ, МОДЕЛИРОВАНИЯ Основные положения Решение дифференциальных уравнений гидродинамики охватывает ограниченный круг задач. В ряде случаев аналитическое решение сопряжено со значительными математическими трудностями. В частности, не всегда можно получить удовлетворительный результат и с помощью численных методов. В таких случаях на помощь приходят экспериментальные методы исследования. Цель этих исследований состоит в том, чтобы получить данные, необходимые для расчета других процессов, родственных изучаемому. Эксперименты проводятся на специально создаваемых модельных установках, моделирующих определенным образом исследуемые устройства и протекающие в них физические процессы. Известны физический и математический методы моделирования. При физическом моделировании исследуемая модель обычно выполняется в меньшем масштабе, чем оригинал (натура), и воспроизводит изучаемое явление с сохранением его физической природы. Математическое моделирование осуществляется путем изучения явлений, имеющих иное, чем исследуемый процесс, физическое содержание, но описываемых аналогичными математическими уравнениями.
|
||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.59.244 (0.008 с.) |



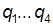 и потерянного напора hv на пути от точки А до точки В.
и потерянного напора hv на пути от точки А до точки В. в узловых точках являются общими для каждой из веток, а их разность
в узловых точках являются общими для каждой из веток, а их разность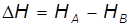 (6.30)
(6.30)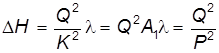 ,
,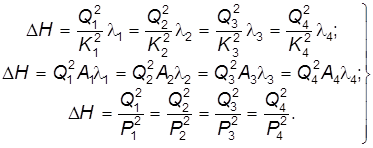 (6.31)
(6.31)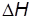 ) четыре уравнения (по числу веток) и пять неизвестных величин, из них четыре неизвестных расхода
) четыре уравнения (по числу веток) и пять неизвестных величин, из них четыре неизвестных расхода  и один неизвестный потерянный напор
и один неизвестный потерянный напор  . (6.32)
. (6.32)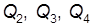 через расход
через расход 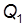 и получим:
и получим: (6.33)
(6.33)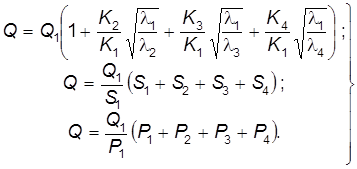 (6.34)
(6.34)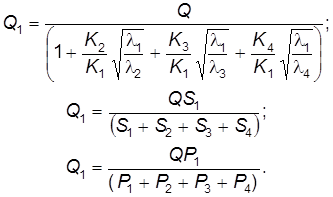 (6.35)
(6.35)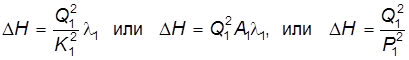 .
.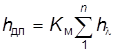 ,
,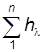 –
–
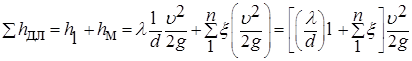 , (6.36)
, (6.36)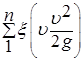 – сумма потерь напора на местных сопротивлениях.
– сумма потерь напора на местных сопротивлениях.
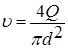 , значение подставим в формулу (6.36) и получим
, значение подставим в формулу (6.36) и получим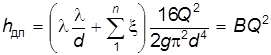 , (6.37)
, (6.37)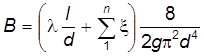 –
–
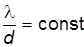 , независимо от диаметра трубопровода, при одних и тех же значениях Q, Sx и l, найдём отношение
, независимо от диаметра трубопровода, при одних и тех же значениях Q, Sx и l, найдём отношение  для диаметров
для диаметров 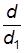 из формулы (6.37):
из формулы (6.37): (6.38)
(6.38) , (6.39)
, (6.39)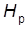 –
–
 или в общем виде
или в общем виде . (6.40)
. (6.40)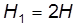 , тогда
, тогда



