
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ламинарная и турбулентная фильтрация
Движение грунтовых вод происходит, как правило, в условиях ламинарного течения. Для расчета таких фильтрационных потоков применяются формулы (8.4) и (8.7). Случай, когда фильтрационный поток имеет значительную скорость, движение будет турбулентным, формулы (8.4) и (8.7) неприемлемы. Случай, когда скорости фильтрации настолько малы, что решающими силами будет не сила тяжести, а молекулярное взаимодействие частиц жидкости с частицами грунта формулы (8.4) и (8.7) также неприемлемы. Таким образом, для формул Дарси существует верхний и нижний предел их применимости. Основной закон фильтрации теряет силу, если скорость фильтрации превышает критическое значение, см/с где Нижний предел применимости формулы Дарси соответствует условию, когда начинает преобладать действие межмолекулярных сил. Турбулентная фильтрация возникает при относительно больших поперечных сечениях паровых каналов. Между ламинарной и квадратичной областью фильтрации лежит широкая область переходных режимов. Граница перехода от ламинарного к турбулентному режиму фильтрации определяется критическим значением числа Рейнольдса: где
Значение числа Рейнольдса критического равно 2780. В квадратичной области фильтрации скорость фильтрации определяется по формуле Для определения скорости фильтрации при турбулентном режиме можно пользоваться формулой С.В. Избаша где
8.5. Основное уравнение неравномерного движения грунтовых вод
В условиях плоской задачи при уклоне дна подстилающего слоя i >0 (грунт однороден) уравнение неравномерного движения имеет вид:
где
 – уклон свободной поверхности по отношению к дну (рис.8.3) – уклон свободной поверхности по отношению к дну (рис.8.3)
Рис. 8.3 Если
означает, что уклон свободной поверхности равняется уклону дна, т.е. поток находится в условиях равномерного режима с глубиной На рисунке 8.4. в потоке с уклоном i > 0 проведем линию n– n, лежащую выше подстилающего слоя на высоте Если Если Если
Рис.8.5
Рис. 8.6
где
При прямом уклоне подстилающего слоя i > 0 (рис. 8.4) применима формула где
При обратном уклоне дна грунтового потока i < 0 где
Расход
ü при прямом уклоне дна (i > 0) ü при нулевом уклоне дна (i = 0) из формулы (8.20) ü при обратном уклоне дна (i < 0)
|
||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.79.59 (0.007 с.) |
 (8.15)
(8.15)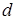 – диаметр частиц грунта.
– диаметр частиц грунта.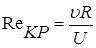 (8.16)
(8.16) – действительная скорость в порах;
– действительная скорость в порах; –гидравлический радиус порового канала;
–гидравлический радиус порового канала; – кинематическая вязкость жидкости.
– кинематическая вязкость жидкости.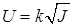 (8.17)
(8.17)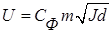 (8.18)
(8.18)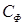 – обобщенный коэффициент Шези, равный 20–14/ d
– обобщенный коэффициент Шези, равный 20–14/ d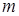 – пористость среды (грунта).
– пористость среды (грунта).
 – глубина потока в рассматриваемом сечении;
– глубина потока в рассматриваемом сечении; – расстояние от рассматриваемого сечения до некоторого начального;
– расстояние от рассматриваемого сечения до некоторого начального;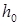 – глубина потока при равномерном режиме;
– глубина потока при равномерном режиме;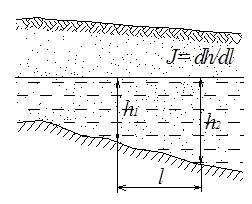
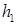 =
= 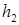 , то
, то 
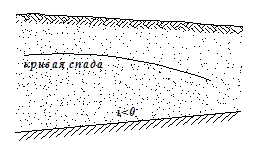 При обратном уклоне подстилающего слоя i < 0 (рис.8.5)
При обратном уклоне подстилающего слоя i < 0 (рис.8.5) 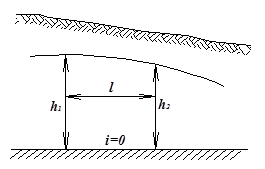 При нулевом уклоне подстилающего слоя i = 0 будет тоже кривая спада, как показано на рис. 8.6. При нулевом уклоне применяется формула Дюпон для построения cвободной поверхности грунтовых вод при неравномерном их движении
При нулевом уклоне подстилающего слоя i = 0 будет тоже кривая спада, как показано на рис. 8.6. При нулевом уклоне применяется формула Дюпон для построения cвободной поверхности грунтовых вод при неравномерном их движении (8.20)
(8.20)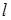 – расстояние между сечениями с глубинами
– расстояние между сечениями с глубинами  и
и  ;
;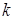 – коэффициент фильтрации;
– коэффициент фильтрации; – удельный расход.
– удельный расход. (8.21)
(8.21)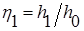 – относительная глубина в первом сечении;
– относительная глубина в первом сечении; – относительная глубина во втором сечении.
– относительная глубина во втором сечении.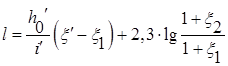 (8.22)
(8.22)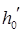 – фиктивная глубина, равная глубине равномерного движения при том же расходе и при положительном уклоне, численно равном данному
– фиктивная глубина, равная глубине равномерного движения при том же расходе и при положительном уклоне, численно равном данному 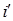 (абсолютное значение данного уклона
(абсолютное значение данного уклона  );
);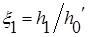 ;
; 
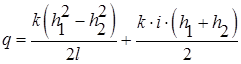 (8.23)
(8.23)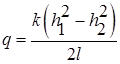 (8.24)
(8.24)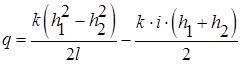 (8.25)
(8.25)


