
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ размерностей. p -теоремаСодержание книги
Поиск на нашем сайте
При организации экспериментов необходимо с самого начала установить наиболее целесообразную методику их проведения и порядок обработки результатов опытов. В практике гидравлических исследований метод анализа размерностей нашел широкое применение. Этот метод позволяет заранее определить основные критерии подобия, в которых следует обрабатывать результаты опытов, а также обобщать их и устанавливать закономерности, отражающие исследуемый процесс. Исходным для метода анализа размерностей является то, что любое математическое уравнение, описывающее физический процесс, обязательно должно быть размерно однородным. Это означает, что обе его части имеют всегда одинаковую размерность независимо от выбора системы физических величин. Свойство однородности является основой теории размерностей. В механике в качестве основных физических величин принимают длину L, массу M и время T. Они независимы друг от друга. В механике жидкости и газа не всегда удается воспользоваться основными физическими величинами, тогда принимаются любые, независимые друг от друга, например плотность, скорость, время. Достоинством метода является то, что при его применении достаточно знать основные переменные величины, характеризующие данный процесс, само же уравнение, описывающее этот процесс, может быть неизвестно. Обычно задача анализа размерностей решается путем определения физических величин, которые полностью характеризуют данный процесс. Затем устанавливается характер зависимости между выделенными величинами, исходя из принципа однородности размерности с помощью так называемой p-теоремы. Сущность p-теоремы состоит в следующем. В общем случае Предположим, что переменная величина А 1 зависит от ряда переменных: А 2, А 3, …, А n, участвующих в каком-либо физическом процессе, и не зависит от каких-либо других переменных. Тогда общая функциональная зависимость между этими величинами может быть представлена уравнением
или
Пусть число определяющих размерных единиц, через которые могут быть выражены все n – переменные, равно m. p-Теорема формулируется так: Уравнение, связывающее между собой n размерных физических величин, характеризующих рассматриваемое явление, среди которых m обладают независимой размерностью, может быть преобразовано в n- m безразмерных комплексов, составленных из указанных величин. p-Теорема устанавливает, что если указанные n переменных выразить через эти основные единицы, то их можно сгруппировать в n - m безразмерных p-членов:
где каждое число p представляет собой безразмерное произведение нескольких А, то есть число членов в физическом уравнении сокращается до n – m. Причем каждый такой p-член будет содержать m + 1 переменную величину. В гидродинамических задачах число таких переменных, входящих в p-члены, должно равняться четырем. Три из них – определяющие: характерный размер (диаметр d), скорость течения жидкости u и ее плотность r (или вязкость m) входят в каждый из p-членов и только четвертая заменяется другой при переходе от члена к члену. Для удобства исследования показатели последних принимаются равными –1. Показатели степени определяющих переменных неизвестны. Обозначим их x, y, z с индексами, соответствующими индексам p-членов. Таким образом, имеем:
Выражаем затем входящие в p-члены переменные через основные независимые размерности, но, поскольку эти члены являются безразмерными во всех полученных для них выражениях, то показатели степени каждой из основных размерностей должны обязательно равняться нулю.
Примеры Пример. Рассмотрим применение p-теоремы для определения опытным путем потерь напора на трение по длине потока при равномерном напорном движении по трубам вязкопластичной бингамовской жидкости. Известно, что потери напора, а следовательно, и давления D p зависят от следующих факторов: – геометрических характеристик трубопровода диаметра d, длины ℓ, шероховатости стенок D; – физических свойств жидкости: плотности r, динамической вяз-кости m, начального напряжения сдвига t0; – средней скорости течения v. Общую функциональную зависимость, связывающую эти величины, представим уравнением:
или
В задачах прикладной механики жидкости и газа имеются три физические величины, имеющие независимые размерности: масса [ M ], время [ T ], длина [ L ], то есть в этих задачах следует принимать m = 3. Это позволяет составить уравнение размерностей для каждого p-члена, соблюдая при этом обязательное условие их размерной однородности. Так как число основных размерных величин равно трем (m = 3), а переменных величин в уравнении (7.32) семь (n = 7), то получим уравнение, состоящее из n - m безразмерных p-членов:
Каждый p-член должен содержать четыре переменные величины. Принимаем в качестве определяющих переменных величин следующие: – диаметр трубопровода d; – среднюю скорость u; – плотность жидкости r. Комбинируя их поочередно с остальными переменными, входящими в уравнение (7.32), получим:
Запишем размерности переменных величин, входящих в p-члены системы (7.34): [ d ] = [ L ]; [ v ] = [m] = [D]=[ L ]; [D p ] = Составим уравнения размерностей для каждого из p-членов, имея в виду обязательное условие их размерной однородности. Для первого члена имеем
Найдем степени размерностей в левой части уравнения (7.35):
Приравнивая к нулю показатели степени при одинаковых основаниях х, получим систему уравнений с неизвестными x 1, y 1, z 1:
Из совместного решения уравнений (7.36) находим:
Подставив эти значения показателей степени в первый p-член системы уравнений (7.34), получим
где найденное значение p1 представляет собой критерий Рейнольдса: Для второго p-члена имеем
Отсюда запишем систему уравнений:
Находим x 2, y 2, z 2:
Запишем выражение для второго p-члена с учетом показателей степени:
или
Для третьего p-члена:
Отсюда
Решая систему уравнений, получим:
Тогда
или
Для четвертого p-члена:
Отсюда
Решая систему уравнений, получим:
Тогда
или
Подставив значения p-членов в соотношение (7.33), получаем уравнение:
Решая уравнение (7.41) относительно p4, находим
Выделим D p из уравнения (7.42) и получим:
Разделив левую и правую части уравнения (7.43) на r g, находим:
Обозначим
и получим выражение для потери напора:
Тогда общее выражение для l примет вид:
Знаменатель выражения (7.44) представляет собой критериальное уравнение, включающее критерии:
Отношение Следовательно, можно выразить l в следующем виде:
Для ньютоновской жидкости t0 = 0, поэтому при турбулентном режиме имеем
При ламинарном режиме (e = 0), тогда
Таким образом, применение метода анализа размерностей позволило выявить основные критерии подобия, характеризующие потери напора на трение по длине трубопровода. В этих критериях производится обработка опытных данных на модели таким образом, чтобы соблюдалось их равенство в натуре.
Контрольные вопросы 1. Сущность частичного моделирования. 2. Сущность частичного моделирования по критерию Рейнольдса. 3. Сущность частичного моделирования по критерию Фруда. 4. Сущность анализа размерностей и его достоинства. 5. Сущность p-теоремы. 6. Какие основные физические величины приняты в механике жидкости и газа? 7. Запишите размерность физических величин r, m, t0, u. 8. Как определяется число p-членов?
|
||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.211.116 (0.008 с.) |

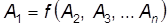 (7.28)
(7.28)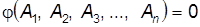 .
.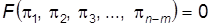 , (7.29)
, (7.29)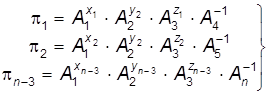 . (7.30)
. (7.30)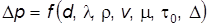 (7.31)
(7.31)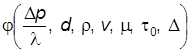 . (7.32)
. (7.32)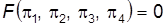 . (7.33)
. (7.33)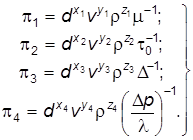 (7.34)
(7.34)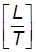 ; [r] =
; [r] =  ;
;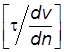 = [ FTL -2] =
= [ FTL -2] = 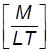 ; [t0] =
; [t0] = 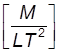 ;
;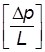 =
= 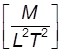 .
.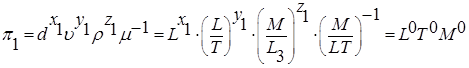 . (7.35)
. (7.35)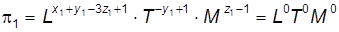 .
.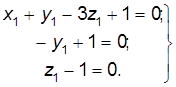 (7.36)
(7.36)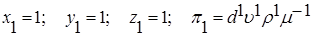 .
. , (7.37)
, (7.37)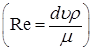 .
.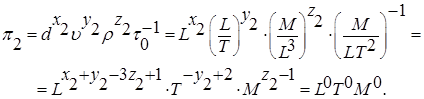


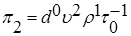
 . (7.38)
. (7.38) ;
;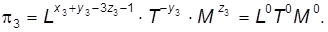
 .
.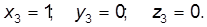

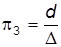 . (7.39)
. (7.39)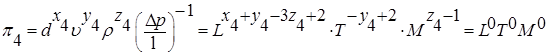 .
. .
.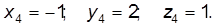
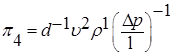
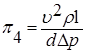 . (7.40)
. (7.40)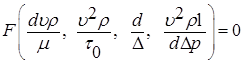 . (7.41)
. (7.41) . (7.42)
. (7.42)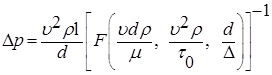 . (7.43)
. (7.43)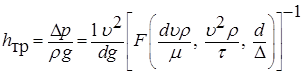 .
.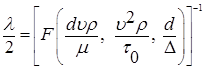
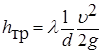 .
.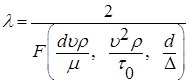 . (7.44)
. (7.44) – критерий Рейнольдса;
– критерий Рейнольдса;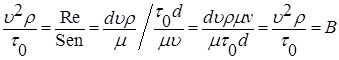 – критерий пластичности;
– критерий пластичности;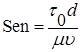 –
–
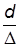 является характеристикой геометрического подобия
является характеристикой геометрического подобия 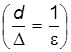 .
.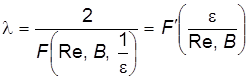 . (7.45)
. (7.45)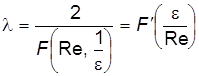 .
.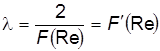 .
.


